Abstract
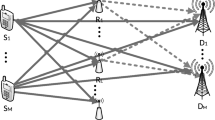
In this paper, we study a User Grouping based Opportunistic Network Coding (UG-ONC) scheme for multi-user multi-relay uplink transmission scenario. In traditional opportunistic network coding (ONC) schemes, the use of network coding is often determined by the state of relays, i.e., buffer, packets waiting time, packets’ successful decoding. However, whether the use of network coding is beneficial to the users is not considered. In our proposed UG-ONC scheme, whether network coding is adopted is not only determined by the state of relays, but also by the link quality between users and base station, that is, determined by the state of users. We consider two information-theoretic metrics, i.e., outage probability and throughput, to evaluate the validity and reliability of the UG-ONC scheme. And the approximate expressions of outage probability and throughput are derived. To further examine the performance of the scheme, we compare UG-ONC scheme with an existent network coding scheme. Monte Carlo simulations are presented to validate our analysis. The results show that our proposed UG-ONC scheme achieves considerable gains over the traditional network coding scheme. Our proposed UG-ONC scheme gives a new thought for designing opportunistic network coding.









Similar content being viewed by others
References
Cover, T., & Gamal, A. E. (1979). Capacity theorems for the relay channel. IEEE Transactions on Information Theory, 25(5), 572–584.
Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part I. System description. IEEE Transactions on Communications, 51(11), 1927–1938.
Xu, Y., Xia, X., Xu, K., & Zhang, D. (2015). On the hybrid relaying protocol for time division broadcasting. Transactions on Emerging Telecommunications Technologies, 26(5), 893–904.
Laneman, J. N., Tse, D. N., & Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50(12), 3062–3080.
Bletsas, A., Khisti, A., Reed, D. P., & Lippman, A. (2006). A simple cooperative diversity method based on network path selection. IEEE Journal on Selected Areas in Communications, 24(3), 659–672.
Xia, X., Xu, K., Ma, W., & Xu, Y. (2013). On the design of relay selection strategy for two-way amplify-and-forward mobile relaying. IET Communications, 7(17), 1948–1957.
Ahlswede, R., Cai, N., Li, S.-Y., & Yeung, R. W. (2000). Network information flow. IEEE Transactions on Information Theory, 46(4), 1204–1216.
Katti, S., Rahul, H., Hu, W., Katabi, D., Mdard, M., & Crowcroft, J. (2006). XORs in the air: practical wireless network coding. In ACM SIGCOMM computer communication review, Vol. 36, 4, pp. 243–254. New York: ACM.
Katti, S., Gollakota, S., & Katabi, D. (2007). Embracing wireless interference: analog network coding. In ACM SIGCOMM computer communication review, Vol. 37, 4, pp. 397–408. New York: ACM.
Zhang, S., Liew, S. C., & Lam, P. P. (2006). Hot topic: Physical-layer network coding. In Proceedings of the 12th annual international conference on mobile computing and networking, (pp. 358–365). New York: ACM.
Xia, X., Xu, Y., Xu, K., Zhang, D., & Li, N. (2013). Outage performance of AF-based time division broadcasting protocol in the presence of co-channel interference. IEEE WCNC 2013, Shanghai, China.
Xu, Y., Xia, X., Xu, K., & Chen, Y. (2013). Symbol error rate of two-way decode-and-forward relaying with co-channel interference. IEEE PIMRC 2013, London.
Ding, Z., & Leung, K. K. (2011). On the combination of cooperative diversity and network coding for wireless uplink transmissions. IEEE Transactions on Vehicular Technology, 60(4), 1590–1601.
Sharma, S., Shi, Y., Liu, J., Hou, Y. T., Kompella, S., & Midkiff, S. F. (2012). Network coding in cooperative communications: Friend or foe? IEEE Transactions on Mobile Computing, 11(7), 1073–1085.
Chen, W., Letaief, K. B., & Cao, Z. (2007). Opportunistic network coding for wireless networks. In IEEE international conference on communications, 2007, ICC’07, (pp. 4634–4639). IEEE.
Katti, S., Katabi, D., Hu, W., Rahul, H., & Medard, M. (2005). The importance of being opportunistic: Practical network coding for wireless environments. In Proceedings of 43rd annual allerton conference on communication, control, and computing.
Chen, W., Letaief, K. B., & Cao, Z. (2012). Buffer-aware network coding for wireless networks. IEEE/ACM Transactions on Networking (TON), 20(5), 1389–1401.
Hsu, Y.-P., Abedini, N., Ramasamy, S., Gautam, N., Sprintson, A., & Shakkottai, S. (2011). Opportunities for network coding: To wait or not to wait. In IEEE international symposium on information theory proceedings (ISIT), 2011, (pp. 791–795). IEEE.
Chieochan, S., Hossain, E., Issariyakul, T., & Niyato, D. (2009). Opportunistic network coding and dynamic buffer allocation in a wireless butterfly network. In Global telecommunications conference, 2009. GLOBECOM 2009. IEEE, Nov. 30–Dec. 4 2009 (pp. 1–6). doi:10.1109/GLOCOM.2009.5425821.
Melvin, S. H., & Ilow, J. (2012). Opportunistic network and erasure coding for asynchronous two-way relay networks. In IEEE global communications conference (GLOBECOM), 2012, (pp. 1739–1744). IEEE.
Hu, J., Fan, P., Xiong, K., Yi, S., & Lei, M. (2011). Cooperation-based opportunistic network coding in wireless butterfly networks. In IEEE global telecommunications conference (GLOBECOM 2011), 2011, (pp. 1–5). IEEE.
Yulong, Z., Jia, Z., & Baoyu, Z. (2013). A fully distributed opportunistic network coding scheme for cellular relay networks. In IEEE Wireless communications and networking conference (WCNC), 2013, 7–10 April 2013 (pp. 2937–2942). doi:10.1109/WCNC.2013.6555028.
Shaohe, L., Weihua, Z., Xiaodong, W., & Xingming, Z. (2011). Scheduling in wireless ad hoc networks with successive interference cancellation. In Proceedings of IEEE on INFOCOM, 2011, 10–15 April 2011 (pp. 1287–1295). doi:10.1109/INFCOM.2011.5934911.
Sung Sik, N., Hasna, M. O., & Alouini, M. S. (2011). Joint statistics of partial sums of ordered exponential variates and performance of GSC RAKE receivers over Rayleigh fading channel. IEEE Transactions on Communications, 59(8), 2241–2253. doi:10.1109/TCOMM.2011.053111.100027.
Lo, T. K. Y. (1999). Maximum ratio transmission. IEEE Transactions on Communications, 47(10), 1458–1461. doi:10.1109/26.795811.
Acknowledgments
This work is supported by Major Research Plan of National Natural Science Foundation of China (No. 91438115), National Natural Science Foundation of China (No. 61371123, No. 61301165), Special Financial Grant of the China Postdoctoral Science foundation (2015T81079), China Postdoctoral Science Foundation (2014M552612), Jiangsu Province Natural Science Foundation (BK2011002, BK2012055) and Jiangsu Postdoctoral Science Foundation (No. 1401178C).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
Proof of Theorem 1
Recall from (23), we could denote the expression \(\Pr \left( x_1 \ge \frac{2^{r}-1}{\rho },\ldots , x_K \ge \frac{2^{r}-1}{\rho }\right) \) on the right hand side as \(\Pr \left( \sum \nolimits _{i\in S} x_i\ge \frac{2^{\Vert S\Vert r}-1}{\rho }, \ \forall \ S\subseteq \llbracket {{\mathcal {T}}_2} \rrbracket , \ \Vert S\Vert =1 \right) \), where \(\Vert S\Vert \) denotes the number of element in S. We can prove it by using mathematical induction. We first prove that
When \(\Vert S\Vert =1\), there are K inequalities, and when \(\Vert S\Vert =1,2\), the total number of inequalities is \(K+\left( {\begin{array}{c}K\\ 2\\ \end{array}} \right) , \left( {\begin{array}{c}K\\ 2\\ \end{array}} \right) \) more inequalities than the probability expression when \(|S|=1\). And these \(\left( {\begin{array}{c}K\\ 2\\ \end{array}} \right) \) inequalities responds to the inequalities that the sum of arbitrary two norm should be larger than \(\frac{2^{2r}-1}{\rho }\). Thus, we could artificially construct \(\left( {\begin{array}{c}K\\ 2\\ \end{array}} \right) -1\) probability expression between \(\Vert S\Vert =1\) and \(\Vert S\Vert =2\) with different numbers of inequalities when \(\Vert S\Vert =2\). Thus, (37) can be proved by proving that these \( \left( {\begin{array}{c}K\\ 2\\ \end{array}} \right) +1\) are all approximately equal, on the base of including all K inequalities when \(|S|=1\). We give demonstration below that
\({\mathcal {D}}_1\) is used here for concision, whose subscript refers to the value of \(\Vert S\Vert \). The difference between the two probabilities can be shown as
When \(\rho \rightarrow \infty , e^{\frac{(2^r-1)^2}{\lambda \rho }}\approx 1+\frac{(2^r-1)^2}{\lambda \rho }+\frac{(2^r-1)^4}{2\lambda ^2\rho ^2}\). Thus it’s obviously that \(\varDelta _1\) is decreasing to zero at high SNR. In the same way, it can be proved that
In this way, (37) can been proved. We then prove that
Just like the way we prove (37). We could prove it by proving that the probability of inequalities with different number of inequalities when \(\Vert S\Vert =q\) are all approximately equal. This is equivalent to prove that
The difference of the two probabilities can be shown as
It is obviously that when \(\rho \rightarrow \infty , \varDelta _{q-1}=0\). Thus, (42) is proved. As a result, the theorem is proved. \(\square \)
Appendix 2
Proof of Theorem 2
To minimize the outage probability, it is equivalent to maximize the probability of \({\mathcal {Q}}\).
According to (18), we treat all packets as unknown except for arbitrary ones, and get the mutual information between users that own these packets and the base station. Different from traditional multiple access channel that all users send pure packets in the same time slot, there are K mixture of packets received in K time slots at the base station, like MIMO [25]. These mixtures are weighted and summed. For arbitrary packet set \({\mathcal {A}}_*\) when \(|{\mathcal {A}}_*|=i\), the combined SNR can be given as below
where \(\llbracket {\mathcal {A}}_*\rrbracket \) denotes the number set of subscript of packets in \({\mathcal {A}}_*\) and \(a_{ni}\) denotes the combination coefficient of mixture from the relay \({\hat{R}}_n\) when all except i packets are treated unknown. Applying MRC [25], \(SNR_{{\mathcal {A}}_*}\) achieves its maximum when
When \(|{\mathcal {A}}_*|=i\), there are \(\left( {\begin{array}{c} K\\ i \end{array}}\right) \) candidate sets for \({\mathcal {A}}_*\). We denote the set that contains all candidate sets as \({\mathcal {A}}_*^i\). Applying (6), (44) and (45) we have
When \({\gamma _{{\hat{R}}_p,n}}={\gamma _{{\hat{R}}_q,n}}\), the equality could be achieved. Accordingly,
Recall from (21), we have
It is obviously that when \(\gamma _{{\hat{R}}_kj}=\frac{1}{\sqrt{K}}\)
That means the probability of \({\mathcal {Q}}_i\) (\(1\le i \le K\)) achieves their maximum at the same time. Thus \(\Pr ({\mathcal {Q}})\) is maximized. According to (26), the minimum of the outage probability is achieved. The theorem is proved. \(\square \)
Rights and permissions
About this article
Cite this article
Wang, J., Xu, Y., Xu, K. et al. A User Grouping Based Opportunistic Network Coding Scheme for Multi-user Multi-relay Uplink Transmissions. Wireless Pers Commun 86, 1629–1652 (2016). https://doi.org/10.1007/s11277-015-3011-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-015-3011-0