Abstract
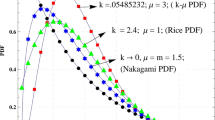
In this paper, the performance of spectrum sharing system in composite Nakagami-m/gamma shadowed channels is analyzed. The environments (of primary and secondary users) corrupted only by noise or interference are considered in details. The novel analytical expressions for outage probability, moment generation function and ergodic capacity are derived in a form of fast-computable Meijer’s G functions, for both mentioned scenarios. Numerical results illustrate the impact of fading and shadowing phenomena on system performance, and appropriate comparison between noise- and interference-limited cases is presented.






Similar content being viewed by others
References
Goldsmith, A., Jafar, S. A., Maric, I., & Srinivasa, S. (2009). Breaking spectrum gridlock with cognitive radios: An information theoretic perspective. Proceedings of the IEEE, 97(5), 894–914.
Mitola, J. (1999). Cognitive radio for flexible mobile multimedia communications. 1999 IEEE international workshop on mobile multimedia communications (MoMuC ‘99), pp. 3–10.
Haykin, S. (2005). Cognitive radio: Brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications, 23(2), 201–220.
Ghasemi, A., & Sousa, E. S. (2008). Spectrum sensing in cognitive radio networks: Requirements, challenges and design trade-offs. IEEE Communications Magazine, 46(4), 32–39.
Ghasemi, A., & Sousa, E. S. (2007). Fundamental limits of spectrum-sharing in fading environments. IEEE Transactions on Wireless Communications, 6(2), 649–658.
Jovicic, A., & Viswanath, P. (2006). Cognitive radio: An information-theoretic perspective. In Proceedings IEEE international symposium on information theory, pp. 2413–2417.
Kang, X., Liang, Y.-C., Nallanathan, A., Garg, H. K., & Zhang, R. (2009). Optimal power allocation for fading channels in cognitive radio networks: Ergodic capacity and outage capacity. IEEE Transactions on Wireless Communications, 8(2), 940–950.
Suraweera, H. A., Smith, P. J., & Shafi, M. (2010). Capacity limits and performance analysis of cognitive radio with imperfect channel knowledge. IEEE Transactions on Vehicular Technology, 59(4), 1811–1822.
Kostic, I. M. (2005). Analytical approach to performance analysis for channel subject to shadowing and fading. IEE Proceeding Communications, 152(6), 821–827.
Shankar, P. M. (2011). Statistical models for fading and shadowed fading channels in wireless systems: A pedagogical perspective. Wireless Personal Communications, 60(2), 191–213.
Bithas, P. S., Sagias, N. C., Mathiopoulos, P. T., Karagiannidis, G. K., et al. (2006). On the performance analysis of digital communications over generalized-K fading channels. IEEE Communications Letters, 10(5), 353–355.
Shankar, P. M. (2004). Error rates in generalized shadowed fading channels. Wireless Personal Communications, 28(3), 233–238.
Rasheed, H., & Rajatheva, N. (2011). Spectrum sensing for cognitive vehicular networks over composite fading. International Journal of Vehicular Technology 9. Article ID 630467.
Hanif, M. F., & Smith, P. J. (2010). On the statistics of cognitive radio capacity in shadowing and fast fading environments. IEEE Transactions on Wireless Communications, 9(2), 844–852.
Gradshteyn, I. S., & Ryzhik, I. M. (1994). Tables of integrals, series, and products (5th ed.). New York: Academic Press.
Adamchik, V. S., & Marichev, O. I. (1990). The algorithm for calculating integrals of hypergeometric type functions and its realization in reduce system. In Proceedings of international symposium on symbolic and algebraic computation, Tokyo, Japan, pp. 212–224.
Prudnikov, A. P., Brychkov, Y. A., & Marichev, O. I. (2003). Integrals and series’, part 3, more special functions (2nd ed.). Moscow: Fizmatlit.
Helstrom, C. W. (1991). Probability and stochastic processes for engineers (2nd ed.). New York: MakMillian.
Acknowledgments
This paper was supported by the Ministry of Science of Republic of Serbia under Grants TR-32028 and III-44006.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
The PDF of the RV z defined as \(z = x_{1} /x_{2}\) can be evaluated using the method given in [18] as
Considering the PDFs given in a form of (4) and representing K k − m (.) by Meijer’s G function as \(K_{\nu } \left( x \right) = \frac{1}{2}G_{0,2}^{2,0} \left( {\frac{{x^{2} }}{4}\left| \begin{aligned} & \_\hfill \\ & \frac{\nu }{2}, - \frac{\nu }{2} \hfill \\ \end{aligned} \right.} \right)\), [17, Eq. (8.4.23.1)], (18) becomes
Integral in (19) can be solved in the exact closed-form, using the procedure of integrating product of two Meijer’s G functions [17, Eq. (2.24.1.1)], in a way
Furthermore, to obtain the PDF of RV \(\gamma^{NL} = c_{1} z\) we use the transformation \(p_{\gamma }^{NL} \left( \gamma \right) = \frac{{p_{z} \left( z \right)}}{{\frac{d\gamma }{{dz}}}}\left| \begin{aligned} \hfill \\ z = \frac{\gamma }{{c_{1} }} \hfill \\ \end{aligned} \right.\) [18], and the PDF of equivalent SNR is derived in the form of (6).
Considering the same procedure as for deriving the PDF p z (z), the PDF of the RV y = z/x 3, can be also obtained. Substituting (20) into \(p_{y} \left( y \right) = \int\limits_{0}^{\infty } {x_{3} p_{z} \left( {yx_{3} } \right)p_{{x_{3} }} \left( {x_{3} } \right)dx_{3} }\), with the help of [17, Eqs. (8.4.23.1), (2.24.1.1)] we get
Finally, the PDF of the RV \(\gamma^{IL} = c_{2} y\) is found, relating to transformation \(p_{\gamma }^{IL} \left( \gamma \right) = \frac{{p_{y} \left( y \right)}}{{\frac{d\gamma }{{dy}}}}\left| \begin{aligned} \hfill \\ y = \frac{\gamma }{{c_{2} }} \hfill \\ \end{aligned} \right.\) [18], in a form given in (8).
Rights and permissions
About this article
Cite this article
Anastasov, J.A., Blagojevic, V.M., Ivanis, P.N. et al. Performance of Spectrum Sharing System in Gamma Shadowed Nakagami-m Fading Environment. Wireless Pers Commun 86, 1717–1729 (2016). https://doi.org/10.1007/s11277-015-3015-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-015-3015-9