Performance Analysis of Hybrid Satellite–Terrestrial Cooperative Systems with Fixed Gain Relaying

Abstract

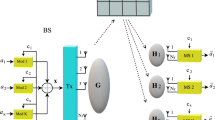
In this paper, we investigate the performance of a hybrid satellite–terrestrial cooperative relay system, where both of the source-relay and source–destination links experience independent non-identical shadowed-Rician fading while the relay-destination link undergoes uncorrelated Rayleigh fading. By employing maximal-ratio-combining at the destination to combine the signals from the direct link and the fixed-gain relay links, we first obtain the analytical expression for the moment generating function (MGF) of the output signal-to-noise ratio (SNR). Then, with the help of the obtained MGF, we derive the theoretical formulas for the ergodic capacity and average symbol error rate of the considered system. Moreover, the asymptotic analysis at high SNR is also presented to reveal the diversity order and array gain of the system. Finally, the effectiveness of the analytical results is verified through comparison with Monte Carlo simulations.

Appendices

Appendix 1: Proof of Theorem 1

By substituting (7) into (11), $E\left[ {\gamma_{sd} } \right],E\left[ {\gamma_{sd}^{2} } \right],E\left[ {\gamma_{i} } \right]$ and $E\left[ {\gamma_{i}^{2} } \right]$ can be calculated as

$$E\left[ {\gamma_{sd} } \right] = \int_{0}^{\infty } {xf_{sd} } \left( x \right)dx = \sum\limits_{n = 0}^{\infty } {\frac{1}{{\left( {n!} \right)^{2} \left( {2b_{0} \gamma_{sd} } \right)^{n + 1} }}} \frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \int_{0}^{\infty } {x^{n + 1} } \exp \left( { - \frac{x}{{2b_{0} \gamma_{sd} }}} \right)dx$$

(41)

$$E\left[ {\gamma_{sd}^{2} } \right] = \int_{0}^{\infty } {x^{2} f_{sd} } \left( x \right)dx = \sum\limits_{n = 0}^{\infty } {\frac{1}{{\left( {n!} \right)^{2} \left( {2b_{0} \gamma_{sd} } \right)^{n + 1} }}} \frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \int_{0}^{\infty } {x^{n + 2} } \exp \left( { - \frac{x}{{2b_{0} \gamma_{sd} }}} \right)dx$$

(42)

With the help of the identity [22]

$$\int_{0}^{\infty } {x^{n} \exp \left( { - ux} \right)dx = n!u^{ - n - 1} }$$

(43)

(41) and (42) can be rewritten as

$$E\left[ {\gamma_{sd} } \right] = \frac{{2b_{0} \gamma_{sd} }}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \sum\limits_{n = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {n + 1} \right)}}} \left( {n + 1} \right)\left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n}$$

(44)

$$E\left[ {\gamma_{sd}^{2} } \right] = \frac{{\left( {2b_{0} \gamma_{sd} } \right)^{2} }}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \sum\limits_{n = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {n + 1} \right)}}} \left( {n + 1} \right)(n + 2)\left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n}$$

(45)

Next, in order to get $E\left[ {\gamma_{i} } \right]$ and $E\left[ {\gamma_{{_{i} }}^{2} } \right]$ we focus on the CDF $\gamma_{i}$ which is given by

$$F_{{\gamma_{i} }} (u) = 1 - \int_{u}^{\infty } {\left[ {1 - F_{{\gamma_{{r_{i} d}} }} \left( {\frac{Cu}{x - u}} \right)} \right]} f_{{\gamma_{{sr_{i} }} }} \left( x \right)dx$$

(46)

where $F_{{\gamma_{{r_{i} d}} }} \left( x \right)$ is the CDF of $\gamma_{{r_{i} d}}$ given by

$$F_{{\gamma_{{r_{i} d}} }} \left( x \right) = 1 - \exp \left( { - \frac{x}{{\gamma_{{r_{i} d}} }}} \right)$$

(47)

By using (7) and (47), (46) can be rewritten as

$$F_{{\gamma_{i} }} \left( u \right) = 1 - \left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \frac{1}{{2b_{0} \gamma_{{sr_{i} }} }}\int_{u}^{\infty } {\exp \left( { - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)} \exp \left( { - \frac{Cu}{{\gamma_{{r_{i} d}} \left( {x - u} \right)}}} \right){}_{1}F_{1} \left( {m_{0} ,1,\frac{\Omega x}{{2b_{0} \gamma_{{sr_{i} }} \left( {2b_{0} m_{0} + \Omega } \right)}}} \right)dx$$

(48)

where ${}_{1}F_{1} \left( {a,b,z} \right)$ represents the confluent hypergeometric function defined as [22]

$${}_{p}F_{q} \left( {a_{1} , \ldots ,a_{p} ;b_{1} , \ldots ,b_{q} ;z} \right) = \sum\limits_{n = 0}^{\infty } {\frac{{\left( {a_{1} } \right)_{n} \ldots \left( {a_{p} } \right)_{n} }}{{\left( {b_{1} } \right)_{n} \ldots \left( {b_{q} } \right)_{n} }}} \frac{{z^{n} }}{n!}$$

(49)

with $\left( x \right)_{n} = x\left( {x + 1} \right)\left( {x + n - 1} \right) = {{\Gamma \left( {x + n} \right)} \mathord{\left/ {\vphantom {{\Gamma \left( {x + n} \right)} {\Gamma \left( x \right)}}} \right. \kern-0pt} {\Gamma \left( x \right)}}$ being the Pochhammer symbol [24]. Thus the $F_{{\gamma_{i} }} \left( \cdot \right)$ could be rewritten as

$$\begin{aligned} F_{{\gamma_{i} }} \left( u \right) & = 1 - \frac{1}{{2b_{0} \gamma_{{sr_{i} }} }}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \int_{u}^{\infty } {\sum\limits_{n = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\left( {n!} \right)^{2} \Gamma \left( {m_{0} } \right)}}} } \left( {\frac{\Omega x}{{2b_{0} \gamma_{{sr_{i} }} \left( {2b_{0} m_{0} + \Omega } \right)}}} \right)^{n} \exp \left( { - \frac{Cu}{{\gamma_{{r_{i} d}} \left( {x - u} \right)}} - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)dx \\ & = 1 - \sum\limits_{n = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\left( {n!} \right)^{2} \Gamma \left( {m_{0} } \right)}}} \frac{{\Omega^{n} \left( {2b_{0} m_{0} } \right)^{{m_{0} }} I_{1} }}{{\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{n + 1} \left( {2b_{0} m_{0} + \Omega } \right)^{{n + m_{0} }} }} \\ \end{aligned}$$

(50)

where

$$\begin{aligned} I_{1} & = \int_{u}^{\infty } {x^{n} \exp \left( { - \frac{Cu}{x - u}\frac{1}{{\gamma_{{r_{i} d}} }} - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)dx} \, \underline{\underline{x - u = t}} \, \int_{0}^{\infty } {\left( {t + u} \right)^{n} \exp \left( { - \frac{Cu}{t}\frac{1}{{\gamma_{{r_{i} d}} }} - \frac{t + u}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)dt} \\ & = \exp \left( { - \frac{\mu }{{2b_{0} \gamma_{{sr_{i} }} }}} \right)\sum\limits_{j = 0}^{n} {\mu^{n - j} } \frac{n!}{{j!\left( {n - j} \right)!}}\int_{0}^{\infty } {t^{j} \exp \left( { - \frac{C\mu }{{\gamma_{{r_{i} d}} }}\frac{1}{t} - \frac{t}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)dt} \\ \end{aligned}$$

(51)

In deriving (51), we have used the formula $\left( {t + u} \right)^{n} = \sum\limits_{j = 0}^{n} {\frac{n!}{{j!\left( {n - j} \right)!}}u^{n - j} } t^{j}$. With the help of the identity [22]

$$\int_{0}^{\infty } {x^{v - 1} } \exp \left( { - \beta x - \frac{\alpha }{x}} \right)dx = 2\left( {\frac{\alpha }{\beta }} \right)^{{\frac{v}{2}}} K_{v} \left( {2\sqrt {\alpha \beta } } \right)$$

(52)

where $K_{n} \left( x \right)$ is the nth order modified Bessel function of the second kind, we have

$$I_{1} = 2\exp \left( { - \frac{u}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)\sum\limits_{j = 0}^{n} {u^{n - j} \frac{n!}{{j!\left( {n - j} \right)!}}} \left( {\frac{{2Cub_{0} \gamma_{{sr_{i} }} }}{{\gamma_{{r_{i} d}} }}} \right)^{{\frac{j + 1}{2}}} K_{j + 1} \left( {2\sqrt {\frac{C}{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} }}u} } \right)$$

(53)

By substituting (53) into (50), after some algebraic manipulations, $F_{{\gamma_{i} }} \left( \mu \right)$ can computed as

$$\begin{aligned} F_{{\gamma_{i} }} \left( x \right) & = 1 - \frac{2}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\frac{1}{{j!\left( {n - j} \right)!}}\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {n + 1} \right)}}} } \left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \\ & \quad \times \left( {\frac{C}{{\gamma_{{r_{i} d}} }}} \right)^{{{{\left( {j + 1} \right)} \mathord{\left/ {\vphantom {{\left( {j + 1} \right)} 2}} \right. \kern-0pt} 2}}} \left( {\frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)^{{n + \frac{1}{2} - \frac{j}{2}}} \exp \left( { - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)K_{j + 1} \left( {2\sqrt {\frac{C}{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} }}x} } \right) \\ \end{aligned}$$

(54)

Using the (54) into (11) with m = 1 and m = 2, respectively, we have

$$\begin{aligned} E\left[ {\gamma_{i} } \right] & = \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\frac{{\left( {{C \mathord{\left/ {\vphantom {C {\gamma_{{r_{i} d}} }}} \right. \kern-0pt} {\gamma_{{r_{i} d}} }}} \right)^{{{{\left( {j + 1} \right)} \mathord{\left/ {\vphantom {{\left( {j + 1} \right)} 2}} \right. \kern-0pt} 2}}} }}{{j!\left( {n - j} \right)!\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{{n - {j \mathord{\left/ {\vphantom {j 2}} \right. \kern-0pt} 2} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} } \\ & \quad \times \frac{{2\Gamma \left( {m_{0} + n} \right)}}{{n!\Gamma \left( {m_{0} } \right)}}\int_{0}^{\infty } {\left[ {x^{{n - \frac{j}{2} + \frac{1}{2}}} \exp \left( { - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)K_{j + 1} \left( {2\sqrt {\frac{C}{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} }}x} } \right)} \right]} dx \\ \end{aligned}$$

(55)

$$\begin{aligned} E\left[ {\gamma_{i}^{2} } \right] & = \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\frac{{\left( {{C \mathord{\left/ {\vphantom {C {\gamma_{{r_{i} d}} }}} \right. \kern-0pt} {\gamma_{{r_{i} d}} }}} \right)^{{{{\left( {j + 1} \right)} \mathord{\left/ {\vphantom {{\left( {j + 1} \right)} 2}} \right. \kern-0pt} 2}}} }}{{j!\left( {n - j} \right)!\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{{n - {j \mathord{\left/ {\vphantom {j 2}} \right. \kern-0pt} 2} + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} }}} \frac{{4\Gamma \left( {m_{0} + n} \right)^{n} }}{{n!\Gamma \left( {m_{0} } \right)}}\left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} } \\ & \quad \times \left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \int_{0}^{\infty } {\left[ {x^{{n - \frac{j}{2} + \frac{3}{2}}} \exp \left( { - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)K_{j + 1} \left( {2\sqrt {\frac{C}{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} }}x} } \right)} \right]} dx \\ \end{aligned}$$

(56)

With the application of the formula [22]

$$\int_{0}^{\infty } {x^{u - 1} \exp \left( { - \alpha x} \right)K_{2v} \left( {2\beta \sqrt x } \right)dx = \exp \left( {\frac{{\beta^{2} }}{2\alpha }} \right)} \alpha^{ - \mu } \frac{{\Gamma \left( {u + \nu + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)\Gamma \left( {u - \nu + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}} \right)}}{2\beta }W_{ - u,\nu } \left( {\frac{{\beta^{2} }}{\alpha }} \right)$$

(57)

where $W_{k,m} \left( \cdot \right)$ is Whittaker function given by [25]

$$W_{k,m} \left( z \right) = z^{{m + \frac{1}{2}}} \exp \left( { - \frac{z}{2}} \right)U\left( {m - k + \frac{1}{2},2m + 1;z} \right)$$

(58)

where $U\left( { \cdot , \cdot ; \cdot } \right)$ is the confluent hypergeometric function of the second kind [22], after some calculation, (55) and (56) can be written as

$$E\left[ {\gamma_{i} } \right] = \left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \sum\limits_{n = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {m_{0} } \right)}}} \frac{{2b_{0} \gamma_{{sr_{i} }} C^{j + 1} (n + 1)}}{{\Gamma \left( {j + 1} \right)}}\left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \sum\limits_{j = 0}^{n} {U\left( {n + 2,j + 2,{C \mathord{\left/ {\vphantom {C {\gamma_{{r_{i} d}} }}} \right. \kern-0pt} {\gamma_{{r_{i} d}} }}} \right)}$$

(59)

$$\begin{aligned} E\left[ {\gamma_{i}^{2} } \right] & = 8b_{0}^{2} \gamma_{{sr_{i} }}^{2} \left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\left( {n + 2} \right)\left( {n + 1} \right)\frac{{\left( {n - j + 1} \right)}}{{\Gamma \left( {j + 1} \right)}}} } \\ & \quad \times \frac{{\Gamma \left( {m_{0} + n} \right)}}{{\Gamma \left( {m_{0} } \right)}}\left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{n} \left( {\frac{C}{{\gamma_{{r_{i} d}} }}} \right)^{j + 1} U\left( {n + 3,j + 2,{C \mathord{\left/ {\vphantom {C {\gamma_{{r_{i} d}} }}} \right. \kern-0pt} {\gamma_{{r_{i} d}} }}} \right) \\ \end{aligned}$$

(60)

Appendix 2: Proof of Theorem 2

The fixed gain constant C in (3) can be written as

$$C = \frac{1}{{G^{2} \sigma_{i}^{2} }} = E\left[ {\left\| {h_{i} } \right\|_{F}^{2} \frac{{P_{s} }}{{\sigma_{i}^{2} }}} \right] + 1 = E\left[ {\gamma_{{sr_{i} }} } \right] + 1$$

(61)

To obtain $E\left[ {\gamma_{{sr_{i} }} } \right]$, we substitute (3) into (8), and yield

$$E\left[ {\gamma_{{sr_{i} }} } \right] = \int_{0}^{\infty } {xf_{{sr_{i} }} } \left( x \right)dx = \sum\limits_{k = 0}^{\infty } {\frac{{\Gamma \left( {m_{0} + k} \right)}}{{\Gamma \left( {m_{0} } \right)}}} \frac{1}{{\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{k + 1} }}\frac{1}{{\left( {k!} \right)^{2} }}\left( {\frac{{2b_{0} m_{0} }}{{2b_{0} m_{0} + \Omega }}} \right)^{{m_{0} }} \left( {\frac{\Omega }{{2b_{0} m_{0} + \Omega }}} \right)^{k} \int_{0}^{\infty } {x^{k + 1} } \exp \left( { - \frac{x}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)dx$$

(62)

With the help of (43), one can obtain

$$E\left[ {\gamma_{{sr_{i} }} } \right] = \sum\limits_{k = 0}^{\infty } {\frac{{2b_{0} \gamma_{{sr_{i} }} \left( {2b_{0} m_{0} } \right)^{{m_{0} }} \left( {k + 1} \right)\Omega^{k} }}{{\left( {2b_{0} m_{0} + \Omega } \right)^{{k + m_{0} }} }}\frac{{\Gamma \left( {m_{0} + k} \right)}}{{k!\Gamma \left( {m_{0} } \right)}}}$$

(63)

The fixed-gain constant C is thus given by

$$C = \sum\limits_{k = 0}^{\infty } {\frac{{2b_{0} {\gamma_{sr}}_{{{i} }} \left( {2b_{0} m_{0} } \right)^{{m_{0} }} \Omega^{k} \left( {k + 1} \right)}}{{\left( {2b_{0} m_{0} + \Omega } \right)^{{k + m_{0} }} }}} \frac{{\Gamma \left( {m_{0} + k} \right)}}{{k!\Gamma \left( {m_{0} } \right)}} + 1$$

(64)

Appendix 3: Proof of Theorem 3

Substituting (46) into (23), after some algebraic manipulations, the expression of $M_{{\gamma_{i} }} \left( s \right)$ is given by

$$M_{{\gamma_{i} }} \left( s \right) = 1 - \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\frac{{2\Gamma \left( {m_{0} + n} \right)s}}{{j!\left( {n - j} \right)!n!\Gamma \left( {m_{0} } \right)\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{{n - \frac{j}{2} + \frac{1}{2}}} }}} } \frac{{\Omega^{n} \left( {2b_{0} m_{0} } \right)^{{m_{0} }} }}{{\left( {2b_{0} m_{0} + \Omega } \right)^{{n + m_{0} }} }}\left( {\frac{C}{{\gamma_{{r_{i} d}} }}} \right)^{{{{\left( {j + 1} \right)} \mathord{\left/ {\vphantom {{\left( {j + 1} \right)} 2}} \right. \kern-0pt} 2}}} I_{2}$$

(65)

where

$$I_{2} = \int_{0}^{\infty } {u^{{n - \frac{j}{2} + \frac{1}{2}}} \exp \left( { - \left( {\frac{{1 + 2b_{0} \gamma_{{sr_{i} }} s}}{{2b_{0} \gamma_{{sr_{i} }} }}} \right)u} \right)} K_{j + 1} \left( {2\sqrt {\frac{C}{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} }}u} } \right)du$$

(66)

By using (57) and (58), it follows that

$$I_{2} = 4\left( {2b_{0} \gamma_{{sr_{i} }} } \right)^{{ - \frac{j}{2} + n - \frac{1}{2}}} \left( {\frac{C}{{\gamma_{{r_{i} d}} }}} \right)^{{\frac{j}{2} + \frac{3}{2}}} \frac{{\left( {n + 1} \right)!\left( {n - j} \right)!}}{{\left( {1 + 2b_{0} \gamma_{{sr_{i} }} s} \right)^{n + 2} }}U\left( {n + 2,j + 2,\frac{C}{{\gamma_{{r_{i} d}} + 2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} s}}} \right)$$

(67)

Substituting (67) into (65), we can get

$$\begin{aligned} M_{{\gamma_{i} }} \left( s \right) & = 1 - \sum\limits_{n = 0}^{\infty } {\sum\limits_{j = 0}^{n} {\frac{{\left( {n + 1} \right)\Gamma \left( {m_{0} + n} \right)}}{{Cj!\Gamma \left( {m_{0} } \right)}}} } \frac{{\Omega^{n} \left( {2b_{0} m_{0} } \right)^{{m_{0} }} }}{{\left( {2b_{0} m_{0} + \Omega } \right)^{{n + m_{0} }} }}\frac{{2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} s}}{{\left( {1 + 2b_{0} \gamma_{{sr_{i} }} s} \right)^{{n - {j \mathord{\left/ {\vphantom {j {2 + 1}}} \right. \kern-0pt} {2 + 1}}}} }} \\ & \quad \times \left( {\frac{{C^{2} }}{{\gamma_{{r_{i} d}}^{2} + 2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}}^{2} s}}} \right)^{{\left( {{j \mathord{\left/ {\vphantom {j 2}} \right. \kern-0pt} 2}} \right) + 1}} U\left( {n + 2,j + 2,\frac{C}{{\gamma_{{r_{i} d}} + 2b_{0} \gamma_{{sr_{i} }} \gamma_{{r_{i} d}} s}}} \right) \\ \end{aligned}$$

(68)