Characterization of IDF and SDF Relaying Protocols in SSK Modulation Systems

Abstract

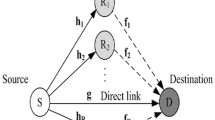
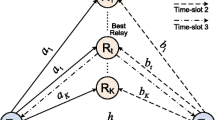
In this paper, the performance of space shift keying (SSK) modulation is investigated in a cooperative communication system, using incremental decode-and-forward (IDF) and selective decode-and-forward (SDF) relays. The IDF and SDF relays use instantaneous signal-to-noise ratio (SNR) to verify the quality of received signal, which is not applicable to SSK modulation. In addition to instantaneous SNR, channel coefficients play the main role in the performance of SSK modulation. Moreover, in this modulation scheme, the active channel coefficient is unknown. In this paper, instead of instantaneous SNR, a new reliable criterion is introduced to be used in the IDF or SDF protocols for SSK modulation. This criterion is based on the Euclidean distances between active channel coefficient and other inactive channel coefficients. The analytical expressions are derived to calculate the average bit error rate (ABER) and the power consumptions in a cooperative system, over Rayleigh fading channels, for both IDF and SDF relaying protocols. There is good agreement between the Monte Carlo simulated and analytical results. These results show that this Euclidean distance-based criterion, in IDF or SDF relaying protocols, improves cooperative diversity gain and the ABER performance significantly.

Appendices

Appendix 1

In this Appendix, it is proved that, for $N_{t}>2$, one of the $x_{min,1}$ or $x_{min,2}$ equals $\left| n \right| ^{2}$ with high probability, where n is the noise of the received signal. Assume that $x_{min}$ is a vector with the elements of $x_{min,q}$ which are the values of $d_{i}$’s in increasing order, where $q=1,2,\ldots ,N_{t}$. The probability that $x_{min,1}=\left| n \right| ^{2}$ is equal to the correct detection probability by optimum detector and is obtained as

$$\begin{aligned} \begin{aligned} Pr\left( x_{min,1}=\left| n \right| ^{2} \right) =1-\left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-1 \right) } \right) ^{-1}. \end{aligned} \end{aligned}$$

(42)

Using the probability theory, the probability that $x_{min,2}=\left| n \right| ^{2}$ is calculated by

$$\begin{aligned}Pr\left( x_{min,2}=\left| n \right| ^{2} \right)=\left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-1 \right) } \right) ^{-1}\quad \times\, \left[ 1-\left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-2 \right) } \right) ^{-1} \right] . \end{aligned}$$

(43)

Therefore, using the probability theory, the general expression of the probability $Pr\left( x_{min,q}=\left| n \right| ^{2} \right)$ is derived as

$$\begin{aligned}Pr\left( x_{min,q}=\left| n \right| ^{2} \right)= \left[ 1-\left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-q \right) } \right) ^{-1} \right] \quad\times\, \prod _{j=1}^{q-1} \left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-j \right) } \right) ^{-1} \end{aligned}$$

(44)

It should be noted that the probability that $x_{min,1}=\left| n \right| ^{2}$ or $x_{min,2}=\left| n \right| ^{2}$ is equal to $\left[ Pr\left( x_{min,1}=\left| n \right| ^{2} \right) +Pr\left( x_{min,2}=\left| n \right| ^{2} \right) \right]$. It is obvious from (44) that $Pr\left( x_{min,q}=\left| n \right| ^{2} \right)$ decreases more with increasing q. For $q>2$ and $\rho _{s}> 10$ dB, the value of $Pr\left( x_{min,q}=\left| n \right| ^{2} \right)$ is negligible in (44), in comparison to the value of $\left[ Pr\left( x_{min,1}=\left| n \right| ^{2} \right) +Pr\left( x_{min,2}=\left| n \right| ^{2} \right) \right]$. Therefore, with high probability one of the $x_{min,1}$ or $x_{min,2}$ is equal to $\left| n \right| ^{2}$.

Appendix 2

In this Appendix, the error probability is derived for SSK modulation with $N_{t}>2$ transmit antennas. Assume the received signal is $y_{sd}$ as presented in (2). The error takes place at the destination detector when

$$\begin{aligned} \begin{aligned} \left| n_{sd} \right| ^{2}>\rho _{s} \mathop {\min }\limits _{i=1,\ldots ,N_{t} , i\ne t }\left\{ \left| h_{t}-h_{i}+\frac{n_{sd}}{\sqrt{\rho _{s}}} \right| ^{2} \right\} . \end{aligned} \end{aligned}$$

(45)

For large values of $\rho _{s}$, the term of $\frac{n_{sd}}{\sqrt{\rho _{s}}}$ is negligible in (45). Then, the right side of (45) is approximated as $\rho _{s} \mathop {\min }\limits _{i}\left\{ \left| h_{t}-h_{i} \right| ^{2} \right\}$. We define w and y as $w=\left| n_{sd} \right| ^{2}$ and $y=\mathop {\min }\limits _{i}\left\{ \left| h_{t}-h_{i} \right| ^{2} \right\}$. As mentioned before in Sect. 3, y is a random variable with PDF given in (26) and w is an exponential random variable with mean $N_{0}$. Therefore, the ASER at the destination is obtained as

$$\begin{aligned} \begin{aligned} P_{s}&=Pr\left( \left| n_{sd} \right| ^{2}>\rho _{s} \mathop {\min }\limits _{i=1,\ldots ,N_{t} , i\ne t }\left\{ \left| h_{t}-h_{i} \right| ^{2} \right\} \right) \\&=\int _{0}^{\infty }\int _{\rho _{s}y}^{\infty }\frac{1}{N_{0}}exp\left( \frac{-w}{N_{0}} \right) f_{Y}\left( y \right) dwdy \\&=\left( 1+\frac{2\sigma _{h}^{2}\rho _{s}}{N_{0}\left( N_{t}-1 \right) } \right) ^{-1} =\left( 1+\frac{2\overline{\gamma } }{N_{t}-1} \right) ^{-1}, \end{aligned} \end{aligned}$$

(46)

where $\overline{\gamma }=\sigma _{h}^{2}\rho _{s}/N_{0}$ is the average received SNR.

Appendix 3

In this Appendix, we want to derive the error probability presented in (35). Using optimum detection, an error will take place at the destination when $\left| n_{sd} \right| ^{2}+\left| n_{r_{j}d} \right| ^{2}>\mathop {\min }\limits _{i=1,\ldots ,N_{t} } \left\{ \left| y_{sd}-\sqrt{\rho }g_{i} \right| ^{2}+\left| y_{r_{j}d}-\sqrt{\rho }f_{j,i} \right| ^{2} \right\}$. We define w as $w=\left| n_{sd} \right| ^{2}+\left| n_{r_{j}d} \right| ^{2}$. The random variable w is sum of two independent exponential random variables with variances of $N_{0}$. The PDF of w is obtained as

$$\begin{aligned} \begin{aligned} f_{W}\left( w \right) =\left( \frac{1}{N_{0}} \right) ^{2}w\,exp\left( \frac{-w}{N_{0}} \right) . \end{aligned} \end{aligned}$$

(47)

As mentioned before, the value of $\mathop {\min }\limits _{i} \left\{ \left| y_{sd}-\sqrt{\rho }g_{i} \right| ^{2}+\left| y_{r_{j}d}-\sqrt{\rho }f_{j,i} \right| ^{2} \right\}$, is approximated as $\rho \mathop {\min }\limits _{i} \left\{ \left| g_{t}-g_{i} \right| ^{2}+\left| f_{j,t}-f_{j,i} \right| ^{2} \right\} =\rho \mathop {\min }\limits _{i} \left\{ r_{i} \right\}$ for large values of $\rho$, where $r_{i}=\left| g_{t}-g_{i} \right| ^{2}+\left| f_{j,t}-f_{j,i} \right| ^{2}$ is sum of two independent exponential random variables, with variances of $2\sigma _{g}^{2}$ and $2\sigma _{f}^{2}$, respectively. The PDFs of $r_{i}$’s are obtained by

$$\begin{aligned} f_{R_{i}}\left( r_{i} \right) = {\left\{ \begin{array}{ll} \left( \frac{1}{2\sigma _{g}^{2}} \right) ^{2}r_{i}\,exp\left( \frac{-r_{i}}{2\sigma _{g}^{2}} \right) &{} 2\sigma _{g}^{2} = 2\sigma _{f}^{2} \\ \frac{exp\left( \frac{-r_{i}}{2\sigma _{f}^{2}} \right) -exp\left( \frac{-r_{i}}{2\sigma _{g}^{2}} \right) }{2\sigma _{f}^{2}-2\sigma _{g}^{2}} &{} 2\sigma _{g}^{2} \ne 2\sigma _{f}^{2}. \end{array}\right. } \end{aligned}$$

(48)

The parameter v is defined as $v=\mathop {\min }\limits _{i=1,\ldots ,N_{t} } \left\{ r_{i} \right\}$. Then, the CDF of v is obtained by

$$\begin{aligned} \begin{aligned} F_{V}\left( v \right)&=Pr\left( \mathop {\min }\limits _{i=1,\ldots ,N_{t} } \left\{ r_{i} \right\} \leqslant v \right) =1-\left[ \int _{v}^{\infty }f_{R_{i}}\left( r_{i} \right) dr_{i} \right] ^{N_{t}-1}. \end{aligned} \end{aligned}$$

(49)

By obtaining the CDF of v, the PDF $f_{V}\left( v \right)$ is calculated as

$$\begin{aligned} \begin{aligned} f_{V}\left( v \right)&=\frac{dF_{V}\left( v \right) }{dv} =\left( N_{t}-1 \right) \left[ \int _{v}^{\infty }f_{R_{i}}\left( r_{i} \right) dr_{i} \right] ^{N_{t}-2} f_{R_{i}}\left( v \right) . \end{aligned} \end{aligned}$$

(50)

Then, substituting (48) into (50) yields (36) and (37) for $2\sigma _{g}^{2}\ne 2\sigma _{f}^{2}$ and $2\sigma _{g}^{2}=2\sigma _{f}^{2}$, respectively. Finally, having $f_{W}\left( w \right)$ from (47) and $f_{V}\left( v \right)$ from (50), $Pr\left( E_{d} \right| C_{r})$ in (35) is completely calculated.