Skip to main content

Advertisement

Springer Nature Link
Log in

A New Equalization Algorithms for Distortion Signal Extraction in Mobile Wireless System

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

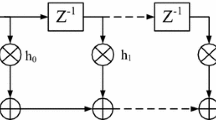
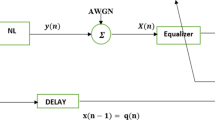
Abstract

In the high-speed mobile wideband communication system, motions of receivers, transmitters or wireless environments generate Doppler frequency. The Doppler effect and instantaneous fading frequency induces serious waveform distortion in the received signal. To solve these problems, the paper presents an improved equalization model, the new model combines the Bayesian detector and decision feedback equalizer (DFE) to form a new effective BDFE structure, which is superior to traditional equalization structure in the mobile environment. Further, a new algorithm is given to achieve faster convergence and smaller steady-state error, the new algorithm take Marr function as a basis function, and two parameters shape the profile of function, with the simulation tool, the optimization values are obtained for the new model and algorithm. The experimental results show that the new algorithm can improve the output SNR up to 6 dB gain with the new BDFE model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Jeong, S., & Moon, J. (2012). Easily computed lower bounds on the information rate of intersymbol interference channels. IEEE Transactions on Information Theory, 58(2), 864–877.

    Article  MathSciNet  MATH  Google Scholar 

  2. Xu, Z., Zhang, H., Hu, C., Mei, L., Xuan, J., Choo, K. R., et al. (2016). Building knowledge base of urban emergency events based on crowdsourcing of social media. Concurrency and Computation Practice and Experience, 28(15), 4038–4052.

    Article  Google Scholar 

  3. Grokop, L. H., & David, N. C. (2009). Diversity–multiplexing tradeoff in ISI channels. IEEE Transactions on Information Theory, 55(1), 109–135.

    Article  MathSciNet  Google Scholar 

  4. Kubo, H., Murakami, K., & Fujino, T. (1994). An adaptive maximum-likelihood sequence estimator for fast time-varying intersymbol interference channels. IEEE Transactions on Communications, 42(234), 1872–1880.

    Article  Google Scholar 

  5. Xu, Z., Zhang, H., Sugumaran, V., Choo, K. R., Mei, L., & Zhu, Y. (2016). Participatory sensing-based semantic and spatial analysis of urban emergency events using mobile social media. EURASIP Journal Wireless Communication and Networking, 2016, 44.

    Article  Google Scholar 

  6. Zhang, G., & Dong, H. (2013). Underwater communications in time-varying sparse channels using passive-phase conjugation. Applied Acoustics, 74(3), 421–424.

    Article  Google Scholar 

  7. Song, H. C., Hodgkiss, W. S., Kuperman, W. A., Stevenson, M., & Akal, T. (2006). Improvement of time-reversal communications using adaptive channel equalizers. IEEE Journal of Oceanic Engineering, 31(2), 487–496.

    Article  Google Scholar 

  8. Rouseff, D., Jackson, D. R., Fox, W. L. J., Jones, C. D., Ritcey, J. A., & Dowling, D. R. (2001). Underwater acoustic communication by passive-phase conjugation: theory and experimental results. IEEE Journal of Oceanic Engineering, 26(4), 821–831.

    Article  Google Scholar 

  9. Yang, T. C. (2004). Differences between passive-phase conjugation and decision-feedback equalizer for underwater acoustic communications. IEEE Journal of Oceanic Engineering, 29(2), 472–487.

    Article  Google Scholar 

  10. Lasaulce, S., Sellami, N., Yuan, Y. & Saadani, A. (2003). Performance study of least-squares channel estimation based on hard decisions. In Proceedings of the Vehicular Technology Conference (vol. 4, pp. 2570–2574). Orlando, FL.

  11. Reddy, B. S. K., & Lakshmi, B. (2015). Improvement in the performance of WiMAX with channel equalizers and space time block coding techniques using simulink. Wireless Personal Communications, 84(4), 2815–2833.

    Article  Google Scholar 

  12. Dowling, D. R. (1994). Acoustic pulse compression using passive phase-conjugate processing. The Journal of the Acoustical Society of America, 95(3), 450–1458.

    Article  Google Scholar 

  13. Adrián-Martínez, S., Al Samarai, I., Albert, A., et al. (2012). Measurement of atmospheric neutrino oscillations with the ANTARES neutrino telescope. Physics Letters B, 714(2), 224–230.

    Article  Google Scholar 

  14. Yang, T. C. (2003). Temporal resolution of time-reversal and passive-phase conjugation for underwater acoustic communications. IEEE Journal of Oceanic Engineering, 28(2), 229–245.

    Article  Google Scholar 

  15. Hursky, P., Porter, M. B., Rice, J. A., & V. K. McDonald, V. K. (2001) Passive phase-conjugate signaling using pulse-position modulation. In Proceeding of the MTS/IEEE OCEANS Conference (vol. 4, pp. 2244–2249). Honolulu, HI.

  16. Al-Dhahir, N., & Cioffi, J. M. (1996). Block transmission over dispersive channels: Transmit filter optimization and realization, and MMSE-DFE receiver performance. IEEE Transactions on Information Theory, 42(1), 137–160.

    Article  MATH  Google Scholar 

  17. Silva, F., Dinis, R., & Montezuma, P. (2015). Frequency-domain receiver design for transmission through multipath channels with strong doppler effects. Wireless Personal Communications, 83(2), 1213–1228.

    Article  Google Scholar 

  18. Wang, J., & He, Q. P. (2007). A bayesian approach for disturbance detection and classification and its application to state estimation in run-to-run control. IEEE Transactions on Semiconductor Manufacturing, 20(2), 126–136.

    Article  Google Scholar 

  19. Seddon, N., & Bearpark, T. (2003). Observation of the inverse Doppler effect. Science, 302(5650), 1537–1540.

    Article  Google Scholar 

  20. Peres, A., & Terno, D. R. (2003). Relativistic Doppler effect in quantum communication. Journal of Modern Optics, 50(6–7), 1165–1173.

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhou, W., Wu, J., & Fan, P. (2015). High mobility wireless communications with Doppler diversity: fundamental performance limits. IEEE Transactions on Wireless Communications, 14(12), 6981–6992.

    Article  Google Scholar 

  22. Xue-Yuan, H., Xiao-Hong, Y., & Li-Xia, Q. (2015). The novel feed forward and decision feedback equalizer structures and improved variable step algorithm. Acta Physica Sinica, 64(23), 0238402. doi:10.7498/aps.64.238402.

  23. Chen, H., Liu, Y., Jiang, W., et al. (2006). A new approach for synthesizing the range profile of moving targets via stepped-frequency waveforms. IEEE Geoscience and Remote Sensing Letters, 3(3), 406–409.

    Article  Google Scholar 

  24. Chen, S., Hanzo, L., & Mulgrew, B. (2001). Decision-feedback equalization using multiple-hyperplane partitioning for detecting ISI-corrupted M-ary PAM signals. IEEE Transactions on Communications, 49(5), 760–764.

    Article  MATH  Google Scholar 

  25. Smith, D. F., Donnelly, T., & Mapps, D. J. (1997). Fixed sample rate Bayesian detector in a variable speed magnetic channel. IEEE Transactions on Magnetics, 33(5), 2797–2799.

    Article  Google Scholar 

  26. Chen, S., McLaughlin, S., Mulgrew, B., et al. (1995). Adaptive Bayesian decision feedback equalizer for dispersive mobile radio channels. IEEE Transactions on Communications, 43(5), 1937–1946.

    Article  Google Scholar 

  27. Qi, Y., & Minka, T. P. (2007). Window-based expectation propagation for adaptive signal detection in flat-fading channels. IEEE Transactions on Communication, 6(1), 348–355.

    Google Scholar 

  28. Kwong, R. H., & Johnston, E. W. (1992). A variable step size LMS algorithm. IEEE Transactions on Signal Processing, 40(7), 1633–1642.

    Article  MATH  Google Scholar 

  29. Li, T. T., Shi, M., & Yi, Q. M. (2011). An improved variable step-size LMS algorithm[C]//Wireless Communications, Networking and Mobile Computing (WiCOM). In 7th International Conference on IEEE (pp. 1–4).

  30. Arablouei, R., & Dogancay, K. (2011). Modified RLS algorithm with enhanced tracking capability for MIMO channel estimation. Electronics Letters, 47(19), 1101–1103.

    Article  Google Scholar 

  31. Sun, P., Zhang, C., Wang, Z., Manchon, C. N., & Fleury, B. H. (2015). Iterative ´ receiver design for ISI channels using combined belief- and expectationpropagation. IEEE Signal Processing Letters, 22(10), 1733–1737.

    Article  Google Scholar 

  32. Badiu, M.-A., Kirkelund, G. E., Manchon, C. N., Riegler, E., & Fleury, B. H. (2012). Message-passing algorithms for channel estimation and decoding using approximate inference. In Proceedings of the IEEE International Symposium Information Theory (pp. 2376–2380).

  33. Aboulnasr, T., & Mayyas, K. (1997). A robust variable step-size LMS-type algorithm: analysis and simulations. IEEE Transactions on Signal Processing, 45(3), 631–639.

    Article  Google Scholar 

  34. Shin, H. C., Sayed, A. H., & Song, W. J. (2004). Variable step-size NLMS and affine projection algorithms. IEEE Signal Processing Letters, 11(2), 132–135.

    Article  Google Scholar 

  35. Wang, W. Wang, Z., Zhang, C., et al. (2016). A BP-MF-EP based iterative receiver for joint phase noise estimation, equalization and decoding. arXiv preprint arXiv:1603.04163.

  36. Gollamudi, S., Nagaraj, S., Kapoor, S., et al. (1998). Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size. IEEE Signal Processing Letters, 5(5), 111–114.

    Article  Google Scholar 

  37. Hwang, J. K., & Li, Y. P. (2009). Variable step-size LMS algorithm with a gradient-based weighted average. IEEE Signal Processing Letters, 12(16), 1043–1046.

    Article  Google Scholar 

  38. Gollamudi, S., Nagaraj, S., Kapoor, S., et al. (1998). Set-membership filtering and a set-membership normalized LMS algorithm with an adaptive step size. IEEE Signal Processing Letters, 5(5), 111–114.

    Article  Google Scholar 

  39. Hong, Y. S., Lee, H., & Tahk, M. J. (2003). Acceleration of the convergence speed of evolutionary algorithms using multi-layer neural networks. Engineering Optimization, 35(1), 91–102.

    Article  MathSciNet  Google Scholar 

  40. Low, S. H., & Lapsley, D. E. (1999). Optimization flow control—I: Basic algorithm and convergence. IEEE/ACM Transactions on Networking (TON), 7(6), 861–874.

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Research Foundation of China grant funded by the China government (11374162) and University Natural Science Project (TJ215009), Nanjing University of Posts and Telecommunications research project (NY215162).

Author information

Authors and Affiliations

  1. Nanjing University of Posts and Telecommunications, Nanjing, 210023, China

    Xue-Yuan Hao & Xiao-Hong Yan

  2. Nanjing University of Information Science & Technology, Nanjing, 210044, China

    Jing Zhao

Authors
  1. Xue-Yuan Hao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiao-Hong Yan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jing Zhao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xue-Yuan Hao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hao, XY., Yan, XH. & Zhao, J. A New Equalization Algorithms for Distortion Signal Extraction in Mobile Wireless System. Wireless Pers Commun 95, 1963–1980 (2017). https://doi.org/10.1007/s11277-016-3869-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-016-3869-5

Keywords