An Opportunistic Source Selection Spectrum Sharing Protocol for Overlay Cognitive Two-Way Relaying System

Abstract

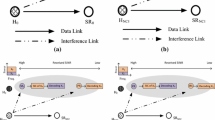
In this paper, an overlay two-way relaying spectrum sharing protocol is proposed by employing an opportunistic source selection strategy. In this protocol, a secondary user acts as a relay and allocates a fraction of its transmit power to assist two-way communication between two primary users (PUs), thus, gaining spectrum sharing as long as without degrading the primary system performance. Moreover, to exploit the multiuser diversity inherent in the multiuser primary systems, the two PUs transmit their own messages in an opportunistic manner, depending on the instantaneous channel conditions. Specifically, at each transaction, only one of the PUs is selected for transmission such that the instantaneous mutual information on the whole primary network is maximized and as a result, the multiuser diversity gain is achieved by the primary system. Then, we derive the exact closed-form outage probabilities for both the primary and secondary systems. To gain more insights, closed-form asymptotic outage probability expressions are also derived. Based on the approximations, we further obtain analytical results on the diversity order of the primary system and the power-allocation threshold above which the spectrum sharing is allowed for secondary transmission. Numerical results are presented to verify our analysis and highlight the advantages of our proposed scheme compared to another two-phase spectrum sharing protocol based on analog network coding.

Appendices

Appendix 1: Proof for Theorem 1

Using the law of total probability, we can write (7) as follows

$$\begin{aligned} \begin{array}{l} P_{CR - OSS}^{PU} = {P_r}\left( {Z< \frac{{{\varTheta _p}}}{{{\eta _p}}},max(X,Y)< \frac{{{\varTheta _p}}}{{{\eta _p}}} } \right) \\ \\ +\,{P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}max(X,Y) }}{{(1 - \alpha ){\eta _s}max(X,Y) + 1}}< {\varTheta _p},\frac{{{\varTheta _p}}}{{{\eta _p}}}< \min (X,Y)< max(X,Y) } \right) \\ \\ +\,{P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}\min (X,Y)}}{{(1 - \alpha ){\eta _s}\min (X,Y) + 1}}< {\varTheta _p},\min (X,Y)< \frac{{{\varTheta _p}}}{{{\eta _p}}} < max(X,Y) } \right) \\ \\ = P_{out}^{ 11} + P_{out}^{ 21} + P_{out}^{ 22} + P_{out}^{ 31} + P_{out}^{ 32} \end{array} \end{aligned}$$

(27)

where

$$\begin{aligned} P_{out}^{ 11}= {P_r}\left( {Z< \frac{{{\varTheta _p}}}{{{\eta _p}}},max(X,Y) < \frac{{{\varTheta _p}}}{{{\eta _p}}} } \right) \end{aligned}$$

(28)

$$\begin{aligned} P_{out}^{ 21}={P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}Y }}{{(1 - \alpha ){\eta _s}Y + 1}}< {\varTheta _p},\frac{{{\varTheta _p}}}{{{\eta _p}}}< X < Y,Y > X } \right) \end{aligned}$$

(29)

$$\begin{aligned} P_{out}^{ 22}={P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}X }}{{(1 - \alpha ){\eta _s}X + 1}}< {\varTheta _p},\frac{{{\varTheta _p}}}{{{\eta _p}}}< Y < X,X > Y } \right) \end{aligned}$$

(30)

$$\begin{aligned} P_{out}^{ 31}={P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}Y}}{{(1 - \alpha ){\eta _s}Y + 1}}< {\varTheta _p},Y< \frac{{{\varTheta _p}}}{{{\eta _p}}} <\,X,X > Y } \right) \end{aligned}$$

(31)

$$\begin{aligned} P_{out}^{ 32}= {P_r}\left( {{\eta _p}Z + \frac{{\alpha {\eta _s}X}}{{(1 - \alpha ){\eta _s}X + 1}}< {\varTheta _p},X< \frac{{{\varTheta _p}}}{{{\eta _p}}} < Y,Y > X } \right) \end{aligned}$$

(32)

Since X, Y, and Z are independent exponential random variables, the term $P_{out}^{11}$ can be straightforwardly derived as

$$\begin{aligned} \begin{array}{l} P_{out}^{11} = \left( {1 - \exp ( - {\lambda _0}\frac{{{\varTheta _p}}}{{{\eta _p}}})} \right) \left( {1 - \exp ( - {\lambda _0}\frac{{{\varTheta _p}}}{{{\eta _p}}})} \right) \left( {1 - \exp ( - {\lambda _0}\frac{{{\varTheta _p}}}{{{\eta _p}}})} \right) \end{array} \end{aligned}$$

(33)

In the following, we will show the derivations of other terms in (27), i.e., $P_{out}^{21}$, $P_{out}^{22}$, $P_{out}^{31}$, and $P_{out}^{31}$.

1.1 Derivations of $P_{out}^{21}$ and $P_{out}^{22}$

Let us come to $P_{out}^{21}$ first. With some manipulations, $P_{out}^{21}$ can be simplified as

$$\begin{aligned} P_{out}^{21} = {P_r}\left( {Z\,<\,f(X), \frac{{{\varTheta _p}}}{{{\eta _p}}}\,<\,Y\,<\,X } \right) \end{aligned}$$

(34)

where $f(\theta ) = {{\left( {{\varTheta _p} - \frac{{\alpha {\eta _s}\theta }}{{(1 - \alpha ){\eta _s}\theta + 1}}} \right) } /{{\eta _p}}}, \theta \in \{ X,Y\}$. Before the calculation of $P_{out}^{21}$, what should be done is to determine the integral region for $P_{out}^{21}$. Let us come to the first condition in $P_{out}^{21}$, i.e., $Z < f(X)$ . To determine the integral in (29), it is important to see that

$$\begin{aligned} f(X)\left\{ \begin{array}{l}> 0, 0< \alpha< {{{\varTheta _p}}/{(1 + {\varTheta _p})}}\\> 0, \alpha> {{{\varTheta _p}}/{(1 + {\varTheta _p})}} and 0< X< \xi \\ < 0, \alpha> {{{\varTheta _p}}/{(1 + {\varTheta _p})}} and X > \xi \end{array} \right. \end{aligned}$$

(35)

where $\xi = \frac{{{\varTheta _p}}}{{[(1 + {\varTheta _p})\alpha - {\varTheta _p}]{\eta _s}}}$.

Since Z is a nonnegative random variable, the value of X must make sure that $f(X) \ge 0$ , otherwise $P_{out}^{ 21} = 0$ if $f(X) < 0$ . Moreover, the second condition in $P_{out}^{21}$ , i.e., ${{{\varTheta _p}}/{{\eta _p}}}< Y < X$ should be also satisfied. Denote $G_{21}^{}(x,y,z)$ as the integral region for $P_{out}^{21}$, and after some simple analysis, $G_{21}^{}(x,y,z)$ can be obtained as follows

$$\begin{aligned} \begin{array}{l} G_{21}^{}(x,y,z) = \left\{ \begin{array}{ll} \{ 0 < Z < f(X),\frac{{{\varTheta _p}}}{{{\eta _p}}} < Y < X\}, & \quad 0 < \alpha < \frac{{{\varTheta _p}}}{{1 + {\varTheta _p}}}\\ \{ 0 < Z < f(X),\frac{{{\varTheta _p}}}{{{\eta _p}}} < Y < X < \xi \}, & \quad \frac{{{\varTheta _p}}}{{1 + {\varTheta _p}}} < \alpha < \frac{{{{{\eta _p}}/ {{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}}\\ \phi, & \quad \frac{{{{{\eta _p}}/{{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}} < \alpha < 1 \end{array} \right. \end{array} \end{aligned}$$

(36)

where ∅ denotes the empty set.

According to (36), we can divide the calculation of $P_{out}^{21}$ into three cases in terms of $\alpha$.

Case I $0< \alpha < {{{\varTheta _p}}/{(1 + {\varTheta _p})}}$

In this case, $P_{out}^{ 21}$ can be calculated by

$$\begin{aligned} P_{out}^{21}&= \{ 0\,<\,Z\,<\, f(X),\frac{{{\varTheta _p}}}{{{\eta _p}}}< Y < X\} \}\nonumber \\&=\int \limits _{{{{\varTheta _p}}/{{\eta _p}}}}^\infty {{\lambda _1}\exp ( - {\lambda _1}x)} dx\int \limits _{{{{\varTheta _p}} /{{\eta _p}}}}^x {{\lambda _2}\exp ( - {\lambda _2}y)} dy\int \limits _0^{f(x)} {{\lambda _0}\exp ( - {\lambda _0}z)} dz\nonumber \\&= \int \limits _{{{{\varTheta _p}}/{{\eta _p}}}}^\infty {{\lambda _1}\exp ( - {\lambda _1}x)\left( {\exp ( - {\lambda _2}\frac{{{\varTheta _p}}}{{{\eta _p}}}) - \exp ( - {\lambda _2}x)} \right) \left( {1 - \exp \left( { - {\lambda _0}f(x)} \right) } \right) dx} \nonumber \\&= \frac{{{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}\exp \left( { - ({\lambda _1} + {\lambda _2})\frac{{{\varTheta _p}}}{{{\eta _p}}}} \right) - \underbrace{\exp ( - {\lambda _2}\frac{{{\varTheta _p}}}{{{\eta _p}}})\int \limits _{{{{\varTheta _p}}/{{\eta _p}}}}^\infty {{\lambda _1}\exp \left( { - {\lambda _1}x - {\lambda _0}f(x)} \right) } dx}_{{\theta _1}} \nonumber \\&\quad + \underbrace{\int \limits _{{{{\varTheta _p}}/{{\eta _p}}}}^\infty {{\lambda _1}\exp \left( { - ({\lambda _1} + {\lambda _2})x - {\lambda _0}f(x)} \right) } dx}_{{\theta _2}} \end{aligned}$$

(37)

Substituting $f(x) = {{\left( {{\varTheta _p} - \frac{{\alpha {\eta _s}x}}{{(1 - \alpha ){\eta _s}x + 1}}} \right) }/{{\eta _p}}}$ into ${\theta _1}$ and making the change of variable $(1 - \alpha ){\eta _s}x + 1 = t$, after some manipulations, the term ${\theta _1}$ can be rewritten as follows

$$\begin{aligned} {\theta _1}&= \frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}\exp \left( { - ({\lambda _0} + {\lambda _2})\frac{{{\varTheta _p}}}{{{\eta _p}}} + \frac{{{\lambda _0}\alpha }}{{(1 - \alpha ){\eta _p}}} + \frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}} \right) \nonumber \\&\quad \underbrace{\int \limits _{\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1}^\infty {\exp \left[ { - \left( {\frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}t + \frac{{\frac{{{\lambda _0}\alpha }}{{(1 - \alpha ){\eta _p}}}}}{t}} \right) } \right] } dt}_\varLambda \end{aligned}$$

(38)

Since we have no closed-form expression for the integral in (38), denoted by $\varLambda$, we tackle this problem by making the change of variable $s = \frac{t}{{{{(1 - \alpha ){\eta _s}{\varTheta _p}}/{{\eta _p}}} + 1 }}$ and applying the Taylor series expansion for the $\exp (\frac{{\frac{{{\lambda _0}\alpha }}{{(1 - \alpha ){\eta _p}}}}}{t})$ within the integral in $\varLambda$, and then after some manipulations, $\varLambda$ can be expressed as follows

$$\begin{aligned} \varLambda&= \int \limits _1^\infty {\sum \limits _{n = 0}^\infty {\frac{{{{( - 1)}^n}{{\left( {\frac{{{\lambda _0}\alpha }}{{(1 - \alpha ){\eta _p}}}} \right) }^n}}}{{n!{{\left( {\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) }^{n - 1}}}}\exp \left( { - \frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}\left( {\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) s} \right) } } ds \nonumber \\&= \sum \limits _{n = 0}^\infty {\frac{{{{( - 1)}^n}{{\left( {\frac{{{\lambda _0}\alpha }}{{(1 - \alpha ){\eta _p}}}} \right) }^n}}}{{n!{{\left( {\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) }^{n - 1}}}}} {E_n}\left( {\frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}\left( {\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) } \right) \end{aligned}$$

(39)

where $E_{n}(\cdot )$ is the exponential integral function.

In order to simplify the notaion, we use a general function ${\varPhi _1}(u,w,\beta )$ defined in Theorem 1 to substitute explicit expression for $\varLambda$. Then, the expression of ${\theta _1}$ can be expressed in a more compact form as

$$\begin{aligned} {\theta _1} = {\varPhi _1}\left( {\frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}, - \frac{{({\lambda _0} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}},\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) \end{aligned}$$

(40)

Taking similar steps as in (38–39), we can obtain the term ${\theta _2}$ in (37) as follows

$$\begin{aligned} {\theta _2} = {\varPhi _1}\left( {\frac{{{\lambda _1}+{\lambda _2}}}{{(1 - \alpha ){\eta _s}}}, - \frac{{{\lambda _0}{\varTheta _p}}}{{{\eta _p}}},\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) \end{aligned}$$

(41)

Substituting (40) and (41) into (37) , we can obtain $P_{out}^{ 21}$ as

$$\begin{aligned} P_{out}^{ 21}&= \frac{{{\lambda _2}}}{{{\lambda _1} + {\lambda _2}}}\exp \left( { - \frac{{({\lambda _1} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}}} \right) \nonumber \\&\quad - {\varPhi _1}\left( {\frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}, - \frac{{({\lambda _0} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}},\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) \nonumber \\&\quad + {\varPhi _1}\left( {\frac{{{\lambda _1} + {\lambda _2}}}{{(1 - \alpha ){\eta _s}}}, - {\lambda _0}\frac{{{\varTheta _p}}}{{{\eta _p}}} ,\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1} \right) \end{aligned}$$

(42)

Case II $\frac{{{\varTheta _p}}}{{1 + {\varTheta _p}}}< \alpha < \frac{{{{{\eta _p}}/{{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}}$

According to $G_{21}^{}(x,y,z)$, we have ${{{\varTheta _p}} / {{\eta _p}}}< Y< X < \xi$. Thus, $P_{out}^{ 21}$ can be calculated by

$$\begin{aligned} P_{out}^{21} = \int \limits _{{{{\varTheta _p}}/{{\eta _p}}}}^\xi {{\lambda _1}\exp ( - {\lambda _1}x)} dx\int \limits _{{{{\varTheta _p}} /{{\eta _p}}}}^x {{\lambda _2}\exp ( - {\lambda _2}y)} dy\int \limits _0^{f(x)} {{\lambda _0}\exp ( - {\lambda _0}z)} dz \end{aligned}$$

(43)

By taking some similar steps employed in Case I such as change of variable and Taylor series expansion, $P_{out}^{ 21}$ in this case can be derived as

$$\begin{aligned} P_{out}^{ 21}&= \frac{{{\lambda _1}}}{{{\lambda _1} + {\lambda _2}}}\left[ {\exp \left( { - ({\lambda _1} + {\lambda _2})\xi } \right) - \exp \left( { - \frac{{({\lambda _1} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}}} \right) } \right] \nonumber \\&\quad + \exp \left( { - \frac{{({\lambda _1} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}}} \right) - \exp \left( { - ({\lambda _1}\xi + \frac{{{\lambda _2}{\varTheta _p}}}{{{\eta _p}}})} \right) \nonumber \\&\quad - {\varPhi _2}\left( {\frac{{{\lambda _1}}}{{(1 - \alpha ){\eta _s}}}, - \frac{{({\lambda _0} + {\lambda _2}){\varTheta _p}}}{{{\eta _p}}},\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1,\xi } \right) \nonumber \\&\quad + {\varPhi _2}\left( {\frac{{{\lambda _1} + {\lambda _2}}}{{(1 - \alpha ){\eta _s}}}, - \frac{{{\lambda _0}{\varTheta _p}}}{{{\eta _p}}} ,\frac{{(1 - \alpha ){\eta _s}{\varTheta _p}}}{{{\eta _p}}} + 1,\xi } \right) \end{aligned}$$

(44)

where $\varPhi _{2}(\cdot )$ is a function which is defined in (12) in Theorem 1.

Case III $\min \left\{ {\frac{{{{{\eta _p}}/ {{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}},1} \right\}< \alpha < 1$

Obviously, in this case $P_{out}^{ 21} = 0$, since the integral region $G_{21}^{}(x,y,z) = \phi$ as it shown in (36).

So far, by combing (42), and (44), a piecewise solution for $P_{out}^{ 21}$ has been obtained in terms of different power allocation factor $\alpha$.

For the term $P_{out}^{ 22}$, the calculation is straightforward. To be specific, one can easily obtain the integral region $G_{22}^{}(x,y,z)$ for $P_{out}^{ 22}$ by interchanging X and Y in (36), i.e., $G_{22}^{}(x,y,z) = G_{21}^{}(y,x,z)$. Moreover, note that the expressions of $P_{out}^{ 21}$ in (29) and $P_{out}^{ 22}$ in (30) are identical in form except that X and Y are interchanged. Hence, the expression $P_{out}^{ 22}$ can be obtained directly by interchanging ${\lambda _1}$ and ${\lambda _2}$ in the expression of $P_{out}^{ 21}$.

1.2 Derivations of $P_{out}^{31}$ and $P_{out}^{32}$

For the term $P_{out}^{ 31}$, the integral region which is denoted by $G_{31}^{}(x,y,z)$ can be obtained as follows

$$\begin{aligned} G_{31}\,(x,y,z) = \left\{ \begin{array}{cc} \{ 0< Z< f(Y),Y< \frac{{{\varTheta _p}}}{{{\eta _p}}}< X\}, &{}\quad 0< \alpha< \frac{{{\varTheta _p}}}{{1 + {\varTheta _p}}}\\ \phi , &{} \quad \frac{{{\varTheta _p}}}{{1 + {\varTheta _p}}}< \alpha< \frac{{{{{\eta _p}}/{{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}}\\ \{ 0< Z< f(Y),Y< \xi< \frac{{{\varTheta _p}}}{{{\eta _p}}}< X\}, &{}\quad \frac{{{{{\eta _p}}/ {{\eta _s}}} + {\varTheta _p}}}{{1 + {\varTheta _p}}}< \alpha < 1 \end{array} \right. \end{aligned}$$

(45)

Furthermore, comparing the probabilities of $P_{out}^{21}$ in (29) and $P_{out}^{31}$ in (31), we notice that the only difference between them is the last two conditions, therefore, the derivation of $P_{out}^{31}$ is analogous to that of $P_{out}^{21}$. Specifically, we also need to divide the derivation into three cases and discuss each case separately. Due to a space limitation, we do not present the derivations of $P_{out}^{31}$. In addition, like the derivation of $P_{out}^{22}$, the expression of $P_{out}^{32}$ can be obtained by interchanging ${\lambda _1}$ and ${\lambda _2}$ in the expression of $P_{out}^{31}$.

Finally, by substituting the closed-form expressions of $P_{out}^{11}$, $P_{out}^{21}$, $P_{out}^{22}$, $P_{out}^{31}$, and $P_{out}^{32}$ into (27), one can obtain a fragment outage probability expression in one-integral form in terms of different $\alpha$ values, as shown in Theorem 1.

Appendix 2: Proof for Lemma 1

We rewrite the function ${\varPhi _1}(u,\omega ,\beta )$ defined in (11) as follows:

$$\begin{aligned} {\varPhi _1}(u,\omega ,\beta ) = u{e^{u + \omega + \beta }}\varPsi (u,\beta ) \end{aligned}$$

(46)

where $\varPsi (u,\beta )$ represents the summation part of (11) and we can further rewrite it as

$$\begin{aligned} \varPsi (u,\beta ) = \frac{{{E_0}(u\beta )}}{{{\beta ^{ - 1}}}} - {v_0}{E_1}(u\beta ) + \sum \limits _{n = 2}^{n = \infty } {\frac{{{{({v_0})}^n}}}{{n!}}\frac{{{E_n}(u\beta )}}{{{\beta ^{n - 1}}}}} \end{aligned}$$

(47)

With the help of [25, eq. 5.1.12], for $n\ge 1$, $E_{n}(u\beta )$ can be expressed as

$$\begin{aligned} {E_n}(u\beta ) = \frac{{{{( - u\beta )}^{n - 1}}}}{{(n - 1)!}}\left[ { - \ln (u\beta ) + \varphi (n)} \right] - \sum \limits _{m = 0, m \ne n- 1}^\infty {\frac{{{{( - u\beta )}^m}}}{{(m - n + 1)m!}}} \end{aligned}$$

where $\varphi (n)$ is the psi function defined in [25, eq. 8.364.5]. Moreover, noting that u, and ${v_0}$ in (11) are functions of ${\rho ^{ - 1}}$ and $\beta$ is independent of ${\rho ^{ - 1}}$, we can see that $u\beta$ is a function of ${\rho ^{ - 1}}$. Thus, the summation term in (47) is an infinitesimal of the secondary order. When $\rho$ is very large, we have the following result

$$\begin{aligned} \varPsi (u,\beta ) = \frac{{{E_0}(u\beta )}}{{{\beta ^{ - 1}}}} - {v_0}{E_1}(u\beta ) + {o}({\rho ^{ - 2}}) \end{aligned}$$

(48)

Furthermore, by taking Taylor expansion, $E_1(u\beta )$ can be expressed as [25, eq.5.1.11]

$$\begin{aligned} {E_1}(u\beta ) = - {\gamma _0} - \ln (u\beta ) + u\beta - \sum \limits _{n = 2}^\infty {\frac{{{{( - 1)}^n}{{(u\beta )}^n}}}{{nn!}}} \end{aligned}$$

(49)

With the help of $E_0(u\beta )=e^{-u\beta }/{u\beta }$ and substituting (49) into (48), we obtain

$$\begin{aligned} \varPsi (u,\beta ) = \frac{{{e^{ - \beta u}}}}{u} + {\gamma _0}{v_0} + {v_0}\ln (\beta u) - \beta u{v_0} + {o}({\rho ^{ - 2}}) \end{aligned}$$

(50)

Then, by substituting (50) into (46) and after some manipulations, we have

$$\begin{aligned} {\varPhi _1}(u,\omega ,\beta )&= u{e^{u + \omega + \beta }}\left( {{{{e^{ - \beta u}}}/u} + {\gamma _0}{v_0} + {v_0}\ln (\beta u) - \beta u{v_0} + {o}({\rho ^{ - 2}})} \right) \nonumber \\&= (1 + u + {v_0} + \omega )(1 - \beta u) + \frac{{{\beta ^2}{u^2}}}{2} + u{v_0}({\gamma _0} + \ln \beta ) + o({\rho ^{ - 3}}) \end{aligned}$$

(51)

where the last equation holds for using the approximation $1-exp(-x) \approx x$ for small x.

On the other hand, if we focus on the first order term in (51), then we can easily express ${\varPhi _1}(u,\omega ,\beta )$ as shown in (13).

Finally, note that ${\varPhi _2}(u,\omega ,\beta ,\gamma ) = {\varPhi _1}(u,\omega ,\beta ) - {\varPhi _1}(u,\omega ,\gamma )$ , thus substituting (51) into the right hand of the forgoing equation yields (14). This completes the proof.