Skip to main content

Advertisement

SpringerLink
Log in

Improving Secrecy Outage and Throughput Performance in Two-Way Energy-Constraint Relaying Networks Under Physical Layer Security

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

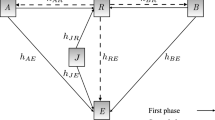
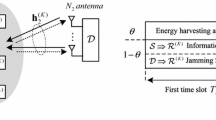
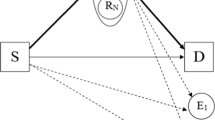
In this paper, we propose three secrecy cooperative transmission protocols for a two-way energy-constrained relaying network in which two sources wish to exchange information with the help of multiple intermediate relays being subjected to wiretapping by multiple eavesdroppers. In the secure two-way communication (STW protocol), an energy-constrained relay is preselected via one of three investigated relay-selection strategies, which harvest the energy from the radio-frequency signals of one source and decode-and-forward the signals to another source. In secure two-way communication with network coding (STWNC protocol), the network coding technique is applied at a relay preselected via one of two investigated relay-selection strategies. In secure two-way communication with cooperative jamming and network coding (STWJNC protocol), under cooperative jamming, the network coding technique is applied at two sources and a preselected relay where a jammer-relay pair is preselected via one of two investigated selection strategies. The power-splitting receiver is applied at the energy-constrained relay for all proposed protocols. To evaluate performance, we derive new closed-form expressions for the secrecy outage probability and the throughput performance of the three protocols with the different relay and jammer-selection strategies. Our analysis is verified using Monte Carlo simulations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Raghunathan, V., Ganeriwal, S., & Srivastava, M. (2006). Emerging techniques for long lived wireless sensor networks. IEEE Communications Magazine, 44(4), 108–114.

    Article  Google Scholar 

  2. Paradiso, J. A., & Starner, T. (2005). Energy scavenging for mobile and wireless electronics. IEEE Pervasive Computing, 4(1), 18–27.

    Article  Google Scholar 

  3. Ulukus, S., Yener, A., Erkip, E., Simeone, O., Zorzi, M., Grover, P., et al. (2015). Energy harvesting wireless communications: A review of recent advances. IEEE Journal on Selected Areas in Communications, 33(3), 360–381.

    Article  Google Scholar 

  4. Medepally, B., & Mehta, N. B. (2010). Voluntary energy harvesting relays and selection in cooperative wireless networks. IEEE Transactions on Wireless Communications, 8(11), 3543–3553.

    Article  Google Scholar 

  5. Zhou, X., Zhang, R., & Ho, C. K. (2013). Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Transactions on communications, 61(11), 4754–4767.

    Article  Google Scholar 

  6. Lumpkins, W. (2014). Nikola Teslas dream realized: Wireless power energy harvesting. IEEE Consumer Electronics Magazine, 3(1), 39–42.

    Article  Google Scholar 

  7. Pinuela, M., Mitcheson, P. D., & Lucyszyn, S. (2013). Ambient RF energy harvesting in urban and semi-urban environments. IEEE Transactions on Microwave Theory and Techniques, 61(7), 2715–2726.

    Article  Google Scholar 

  8. Grover, P., & Sahai, A. (2010). Shannon meet Tesla: Wireless information and power transfer. In IEEE international symposium on information theory proceedings (ISIT), pp. 2363–2367.

  9. Zhang, R., & Ho, C. K. (2013). MIMO broadcasting for simultaneous wireless information and power transfer. IEEE Transactions on Wireless Communications, 12(5), 1989–2001.

    Article  Google Scholar 

  10. Varshney, L. R. (2008). Transporting information and energy simultaneously. In IEEE international symposium on information theory (ISIT), pp. 1612–1616.

  11. Liu, L., Zhang, R., & Chua, K. C. (2013). Wireless information transfer with opportunistic energy harvesting. IEEE Transactions on Wireless Communications, 12(1), 288–300.

    Article  Google Scholar 

  12. Nasir, A. A., Xiangyun, Z., Durrani, S., & Kennedy, R. A. (2013). Relaying protocols for wireless energy harvesting and information processing. IEEE Transactions on Wireless Communications, 12(7), 3622–3636.

    Article  Google Scholar 

  13. Nasir, A. A., Zhou, X., Durrani, S., & Kennedy, R. A. (2015). Wireless-powered relays in cooperative communications: Time-switching relaying protocols and throughput analysis. IEEE Transactions on Communications, 63(5), 1607–1622.

    Article  Google Scholar 

  14. Ding, Z., Perlaza, S. M., Esnaola, I., & Poor, H. V. (2014). Power allocation strategies in energy harvesting wireless cooperative networks. IEEE Transactions on Wireless Communications, 13(2), 846–860.

    Article  Google Scholar 

  15. Liu, Y., Wang, L., Elkashlan, M., & Duong, T. Q. (2014). Two-way relaying networks with wireless power transfer: Policies design and throughput analysis. In IEEE global communications conference (GLOBECOM), pp. 4030–4035.

  16. Son, P. N., & Kong, H. Y. (2015). Energy-harvesting relay selection schemes for decode-and-forward dual-hop networks. IEICE Transactions on Communications, E98-B(4), 661–672.

  17. Stallings, W. (2003). Cryptography and network security principles and practices (3rd ed.). Upper Saddle River, NJ: Prentice Hall.

    Google Scholar 

  18. Wyner, A. D. (1975). The wire-tap channel. The Bell System Technical Journal, 54(8), 1355–1387.

    Article  MathSciNet  MATH  Google Scholar 

  19. Leung-Yan-Cheong, S., & Hellman, M. E. (1978). The Gaussian wire-tap channel. IEEE Transaction on Information Theory, 24(4), 451–456.

    Article  MathSciNet  MATH  Google Scholar 

  20. Csiszar, I., & Korner, J. (1978). Broadcast channels with confidential messages. IEEE Transactions on Information Theory, 24(3), 339–348.

    Article  MathSciNet  MATH  Google Scholar 

  21. Liang, Y., Poor, H. V., & Shamai, S. (2008). Secure communication over fading channels. IEEE Transactions on Information Theory, 54(6), 2470–2492.

    Article  MathSciNet  MATH  Google Scholar 

  22. Dong, L., Han, Z., Petropulu, A. P., & Poor, H. V. (2010). Improving wireless physical layer security via cooperating relays. IEEE Transactions on Signal Processing, 58(3), 1875–1888.

    Article  MathSciNet  Google Scholar 

  23. Zang, R., Song, L., Han, Z., Jiao, B., & Debbah, M. (2010). Physical layer security for for two way relay communications with friendly jammers. In: IEEE global telecommunications conference (GLOBECOM), pp. 1–6.

  24. Wang, L., Elkashlan, M., Huang, J., Tran, N. H., & Duong, T. Q. (2014). Secure transmission with optimal power allocation in untrusted relay networks. IEEE Wireless Communications Letters, 3(3), 289–292.

    Article  Google Scholar 

  25. Wang, L., Kim, K. J., Duong, T. Q., Elkashlan, M., & Poor, H. V. (2014). On the security of cooperative single carrier systems. In IEEE global telecommunications conference (GLOBECOM), Austin, TX, pp. 1596–1601.

  26. Duong, T. Q., Duy, T. T., Elkashlan, M., Tran, N. H., & Dobre, O. A. (2014). Secured cooperative cognitive radio networks with relay selection. In IEEE global telecommunications conference (GLOBECOM), Austin, TX, pp. 3074–3079.

  27. Liu, Y., Wang, L., Duy, T. T., Elkashlan, M., & Duong, T. Q. (2015). Relay selection for security enhancement in cognitive relay networks. IEEE Wireless Communication Letters, 4(1), 46–49.

    Article  Google Scholar 

  28. Jong-Ho, L. (2015). Cooperative relaying protocol for improving physical layer security in wireless decode-and-forward relaying networks. Wireless Personal Communications, 83(4), 3033–3044.

    Article  Google Scholar 

  29. Krikidis, I., Thompson, J. S., & Mclaughlin, S. (2009). Relay selection for secure cooperative networks with jamming. IEEE Transactions on Wireless Communications, 8(10), 50035011.

    Article  Google Scholar 

  30. Long, H., Xiang, W., Wang, J., Zhang, Y., & Wang, W. (2014). Cooperative jamming and power allocation with untrusty two-way relay nodes. IET Communications, 8(13), 2290–2297.

    Article  Google Scholar 

  31. Duy, T. T., Duong, T. Q., Benevides da Costa, D., Bao, V. N. Q., & Elkashlan, M. (2015). Proactive relay selection with joint impact of hardware impairment and co-channel interference. IEEE Transaction on Communications, 64(5), 1594–1606.

    Article  Google Scholar 

  32. Gradshteyn, I. S., Ryzhik, I. M., Jeffrey, A., & Zwillinger, D. (2007). Table of integral, series and products (7th ed.). London: Academic Press.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Duy Tan University, Da Nang, Vietnam

    Sang Quang Nguyen

  2. University of Ulsan, Ulsan, Republic of Korea

    Hyung Yun Kong

Authors
  1. Sang Quang Nguyen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hyung Yun Kong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sang Quang Nguyen.

Appendices

Appendix 1: The PDF of RVs \({\varvec{g_{{R_s}E\max }}}\), \({\varvec{g_{S2E\max }}}\), and \({\varvec{g_{S1E\max }}}\) When Using the Relay Selection Strategy in (19a)

The CDFs of RVs \({g_{{R_s}E\max }}\), \({g_{S2E\max }}\), and \({g_{S1E\max }}\) can be given respectively as

$$\begin{aligned} {F_{{g_{{R_s}E\max }}}}\left( x \right)& = \Pr \left[ {\mathop {\min }\limits _{m = 1,2,\ldots ,M} \left( {\mathop {\max }\limits _{l = 1,2,\ldots ,L} {g_{{R_m}{E_l}}}} \right)< x} \right] \nonumber \\& = 1 - \prod \limits _{m = 1}^M {\left\{ {1 - \prod \limits _{l = 1}^L {\Pr \left[ {{g_{{R_m}{E_l}}} < x} \right] } } \right\} } = 1 - {\left[ {1 - {{\left( {1 - {e^{ - {\lambda _{RE}}x}}} \right) }^L}} \right] ^M} \end{aligned}$$
(66)
$$\begin{aligned} {F_{{g_{S2E\max }}}}\left( x \right)& = \Pr \left[ {\mathop {\max }\limits _{m = 1,2,\ldots ,L} {g_{S2E{\mathop {\mathrm {m}}\nolimits } }} < x} \right] = {\left( {1 - {e^{ - {\lambda _{S2E}}x}}} \right) ^L} \end{aligned}$$
(67)
$$\begin{aligned} {F_{{g_{S1E\max }}}}( x )& = \Pr \left[ {{g_{S1E\max }} < x} \right] = {\left( {1 - {e^{ - {\lambda _{S1E}}x}}} \right) ^L} \end{aligned}$$
(68)

Then, by differentiating (66), (67), and (68), we obtain the PDFs of RVs \({g_{{R_s}E\max }}\), \({g_{S2E\max }}\), and \({g_{S1E\max }}\), respectively, as follows:

$$\begin{aligned} {f_{{g_{{R_s} E\max }}}} \left( x \right)& = M L{\lambda _{RE}}{e^{ - {\lambda _{RE}}x}}{\left( {1 - {e^{ - {\lambda _{RE}}x}}} \right) ^{L - 1}}{\left[ {1 - {{\left( {1 - {e^{ - {\lambda _{RE}}x}}} \right) }^L}} \right] ^{M- 1}}\nonumber \\& = M L{\lambda _{RE}} \sum \limits _{k = 0}^{L - 1} {C_{L - 1}^k} {\left( { - 1} \right) ^k} \sum \limits _{u = 0}^{M - 1} {C_{M - 1}^u} {\left( { - 1} \right) ^u}\sum \limits _{v = 0}^{Lu} {C_{Lu}^v} {\left( { - 1} \right) ^v}{e^{ - \left( {1 + k + v} \right) {\lambda _{RE}}x}} \end{aligned}$$
(69)
$$\begin{aligned} {f_{{g_{S2E\max }}}}\left( x \right)& = L{\lambda _{S2E}}{e^{ - {\lambda _{S2E}}x}}{\left( {1 - {e^{ - {\lambda _{S2E}}x}}} \right) ^{L - 1}}\nonumber \\& = L{\lambda _{S2E}}\sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {\left( { - 1} \right) ^w}{e^{ - \left( {1 + k} \right) {\lambda _{S2E}}x}} \end{aligned}$$
(70)
$$\begin{aligned} {f_{{g_{S1E\max }}}}\left( x \right)& = L{\lambda _{S1E}}{e^{ - {\lambda _{S1E}}x}}{\left( {1 - {e^{ - {\lambda _{S1E}}x}}} \right) ^{L - 1}}\nonumber \\& = L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {\left( { - 1} \right) ^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}x}}. \end{aligned}$$
(71)

Appendix 2: Proof of Lemma 1

At first, the integral \({I_{{\mathrm{1,MAS1R}}}}\) can be expressed as

$$\begin{aligned}&{I_{1,\mathrm{MAS1R}}}\mathop = \limits ^{\left( {{\mathrm{72}}{\mathrm{.1}}} \right) } {e^{ \frac{{ - \left( {\varphi - 1} \right) {\lambda _{S2R}}}}{{{\omega _2}\psi }}}}\int _0^\infty {L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}} \nonumber \\&\quad \int _0^\infty {L{\lambda _{S2E}}\sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left[ {\frac{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}{{{\omega _2}}}} \right] {x_2}}}} \nonumber \\&\quad \int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {M {\lambda _{S1 R}} \sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}{e^{\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}}}}} d{x_3}d{x_2}d{x_1}\nonumber \\&\qquad \mathop \approx \limits ^{\left( {{\mathrm{72}}{\mathrm{.2}}} \right) } {e^{\frac{{ - \left( {\varphi - 1} \right) {\lambda _{S2R}}}}{{{\omega _2}\psi }}}}\left( {{I_3} + {I_4}} \right) \end{aligned}$$
(72)

where (72.2) is obtained by approximating \({e^{\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}}}} \approx 1 + \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}}\).

The term \({I_3}\) and \({I_4}\) in (72) are denoted and derived as in (73) and (74) as follows

$$\begin{aligned}&{I_3} \buildrel \varDelta \over = \int _0^\infty {L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}} \nonumber \\&\qquad \int _0^\infty {L{\lambda _{S2E}}\sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left[ {\frac{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}{{{\omega _2}}}} \right] {x_2}}}} \nonumber \\&\qquad \int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {M{\lambda _{S1R}}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}} d{x_3}d{x_2}d{x_1}\nonumber \\&\quad = L{\lambda _{S2E}}\sum \limits _{w = 0}^{L - 1} {\frac{{C_{L - 1}^w{{\left( { - 1} \right) }^w}{\omega _2}}}{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}} \nonumber \\&\qquad LM{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {\left( { - 1} \right) ^t}\sum \limits _{k = 0}^{M - 1} {\frac{{C_{M - 1}^k{{\left( { - 1} \right) }^k}{\omega _2}{e^{\frac{{ - \left( {1 + k} \right) \left( {\varphi - 1} \right) {\lambda _{S1R}}}}{{{\omega _2}\psi }}}}}}{{\left( {1 + k} \right) \left[ {\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}} + \left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}} \right] }}} \nonumber \\&\quad \buildrel \varDelta \over = {\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) {\varOmega _4}\left( {L,M,\varphi ,{\omega _1},{\omega _2},\psi ,{\lambda _{S1R}},{\lambda _{S1E}}} \right) \end{aligned}$$
(73)
$$\begin{aligned}&{I_4} \buildrel \varDelta \over = \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}\int _0^\infty {L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}} \nonumber \\&\qquad \int _0^\infty {L{\lambda _{S2E}}\sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left[ {\frac{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}{{{\omega _2}}}} \right] {x_2}}}}\nonumber \\&\qquad \int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {M{\lambda _{S1R}}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}\frac{{{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}}}{{{x_3}}}} d{x_3}d{x_2}d{x_1}\nonumber \\& \mathop = \limits ^{\left( {{\mathrm{74}}{\mathrm{.1}}} \right) } \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}{\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \nonumber \\&\qquad \int _0^\infty {L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}}\nonumber \\&\qquad M{\lambda _{S1R}}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}\varGamma \left[ {0,\left( {1 + k} \right) {\lambda _{S1R}}\left( {\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}} \right) } \right] d{x_1}\nonumber \\& \mathop \approx \limits ^{\left( {{\mathrm{74}}{\mathrm{.2}}} \right) } \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}{\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \nonumber \\&\qquad \int _0^\infty {LM{\lambda _{S1E}}{\lambda _{S1R}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}} {e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}\nonumber \\&\qquad \varGamma \left[ {0,\frac{{\left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}{x_1}}}{{{\omega _2}}}} \right] d{x_1}\nonumber \\& \mathop = \limits ^{\left( {{\mathrm{74}}{\mathrm{.3}}} \right) } \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}{\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \nonumber \\&\qquad LM{\lambda _{S1E}}{\lambda _{S1R}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t{{\left( { - 1} \right) }^t}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}} \nonumber \\&\qquad \frac{{{\omega _2}}}{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}} + \left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}}}_2{F_1}\left( {1,1;2;\frac{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}}}}{{\left( {1 + t} \right) {\omega _2}{\lambda _{S1E}} + \left( {1 + k} \right) \varphi {\omega _1}{\lambda _{S1R}}}}} \right) \nonumber \\& \buildrel \varDelta \over = \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}{\varOmega _3}\left( {L,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \nonumber \\&\qquad {\varOmega _5}\left( {L,M,\varphi ,{\omega _1},{\omega _2},{\lambda _{S1R}},{\lambda _{S1E}}} \right) \end{aligned}$$
(74)

where (74.1) is obtained from by using \(\int _0^\infty {L{\lambda _{S2 E}} \sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left[ {\frac{{\left( {1 + w} \right) {\omega _2}{\lambda _{S2E}} + \varphi {\omega _1}{\lambda _{S2R}}}}{{{\omega _2}}}} \right] {x_2}}}} = {\varOmega _3} \left( { L, \varphi , {\omega _1}, {\omega _2},{\lambda _{S2 R}}, {\lambda _{S2 E}}} \right)\) and \(\int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {\frac{{{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}}}{{{x_3}}}} d{x_3} = \varGamma \left[ {0,\left( {1 + k} \right) {\lambda _{S1R}}\left( {\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}} \right) } \right]\) (see [32, Eq. (3.381.3)]); (74.2) is obtained from (74.1) by approximating \(\frac{{\varphi - 1}}{{{\omega _2}\psi }}\mathop \approx \limits ^{{\mathrm{high}}\,\,\psi \,} 0\); (73.3) is obtained from (74.2) by using the Eq. (6.455.1) of [32] in the case of \(\mu = 1\) and \(v = 0\), as \(\int _0^\infty {{e^{ - \beta x}}} \varGamma \left( {0,\alpha x} \right) dx = \frac{1}{{\alpha + \beta }}_2{F_1}\left( {1,\,1\,;\,2\,;\frac{\beta }{{\alpha + \beta }}} \right).\)

We finish the proof by combining (72), (73), and (74).

Appendix 3: Proof of Lemma 2

The integral \({I_{2,\mathrm{MAS1R}}}\) can be obtained after some steps with using [32, Eq. (3.381.3)] and approximating \(\frac{{\varphi - 1}}{{{\omega _2}\psi }} \approx 0\), and \(\frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi {x_3}}} \approx 0\) when \(\psi\) is high, as follows

$$\begin{aligned} {I_{2,maS1R}} \approx \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS1}}}}{{{\omega _3}\psi }}\left( {{I_5} + {I_6}} \right) \end{aligned}$$
(75)

where \({I_5}\) and \({I_6}\) are denoted and derived as in (76) and (77), respectively

$$\begin{aligned}&{I_5} \buildrel \varDelta \over = \int _0^\infty {L{\lambda _{S1E}}\sum \limits _{u = 0}^{L - 1} {C_{L - 1}^u} {{\left( { - 1} \right) }^u}{e^{ - \left( {1 + u} \right) {\lambda _{S1E}}{x_1}}}} \nonumber \\&\qquad \int _0^\infty {L{\lambda _{S2E}}{\lambda _{S2R}}\sum \limits _{k = 0}^{L - 1} {C_{L - 1}^k} {{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{S2E}}{x_2}}}\varGamma \left[ {0,\frac{{\varphi {\omega _1}{\lambda _{S2R}}{x_2}}}{{{\omega _2}}}} \right] } \nonumber \\&\qquad \int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {{\lambda _{S1R}}{e^{ - {\lambda _{S1R}}{x_3}}}} d{x_3}d{x_2}d{x_1}\nonumber \\& = {\varOmega _4}\left( {L,M,\varphi ,{\omega _1},{\omega _2},\psi ,{\lambda _{S1R}},{\lambda _{S 1 E}}} \right) {\varOmega _5} \left( {L, 1, \varphi , {\omega _1}, {\omega _2},{\lambda _{S 2R}},{\lambda _{S 2E}}} \right) \end{aligned}$$
(76)
$$\begin{aligned}&{I_6} \buildrel \varDelta \over = \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}\int _0^\infty {L{\lambda _{S1E}}\sum \limits _{t = 0}^{L - 1} {C_{L - 1}^t} {{\left( { - 1} \right) }^t}{e^{ - \left( {1 + t} \right) {\lambda _{S1E}}{x_1}}}} \nonumber \\&\qquad \int _0^\infty {L{\lambda _{S 2 E}}{\lambda _{S 2 R}} \sum \limits _{w = 0}^{L - 1} {C_{L - 1}^w} {{\left( { - 1} \right) }^w}{e^{ - \left( {1 + w} \right) {\lambda _{S2E}}{x_2}}}\varGamma \left[ {0,\frac{{\varphi {\omega _1}{\lambda _{S2R}}{x_2}}}{{{\omega _2}}}} \right] } \nonumber \\&\qquad \int _{\frac{{\varphi - 1}}{{{\omega _2}\psi }} + \frac{{\varphi {\omega _1}{x_1}}}{{{\omega _2}}}}^\infty {M{\lambda _{S1R}}\sum \limits _{k = 0}^{M - 1} {C_{M - 1}^k} {{\left( { - 1} \right) }^k}\frac{{{e^{ - \left( {1 + k} \right) {\lambda _{S1R}}{x_3}}}}}{{{x_3}}}} d{x_3}d{x_2}d{x_1}\nonumber \\& = \frac{{ - \left( {\varphi - 1} \right) {\lambda _{RS2}}}}{{{\omega _3}\psi }}{\varOmega _5}\left( {L,M,\varphi ,{\omega _1},{\omega _2},{\lambda _{S1R}},{\lambda _{S1E}}} \right) \nonumber \\&\qquad {\varOmega _5}\left( {L,1,\varphi ,{\omega _1},{\omega _2},{\lambda _{S2R}},{\lambda _{S2E}}} \right) \end{aligned}$$
(77)

We finish the proof by combining (75), (76), and (77).

Appendix 4: Proof of Equation (59.2)

The expression for the probability term \(\Pr \left[ {\min \left( {{C_{{J_1}S1}},{C_{{J_1}S2}}} \right) \ge {C_t}} \right]\) can be obtained as follows:

$$\begin{aligned}&\Pr \left[ {\min \left( {{C_{{J_s}S1}},{C_{{J_s}S2}}} \right) \ge {C_t}} \right] \nonumber \\&\quad = \Pr \left[ {{g_{{J_s}S1}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {g_{{J_s}E\max }}} \right] \Pr \left[ {{g_{{J_s}S2}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {g_{{J_s}E\max }}} \right] \nonumber \\&\quad = {e^{\frac{{ - \left( {\varphi - 1} \right) \left( {{\lambda _{JS1}} + {\lambda _{JS2}}} \right) }}{{{\omega _1}\psi }}}}L{\lambda _{JE}}\sum \limits _{k = 0}^{L - 1} {\frac{{C_{L - 1}^k{{\left( { - 1} \right) }^k}}}{{\left( {1 + k} \right) \left( {{\lambda _{JE}} + {\lambda _{JE}}} \right) + \varphi \left( {{\lambda _{JS1}} + {\lambda _{JS2}}} \right) }}} \nonumber \\&\quad = {e^{\frac{{ - \left( {\varphi - 1} \right) \left( {{\lambda _{JS1}} + {\lambda _{JS2}}} \right) }}{{{\omega _1}\psi }}}}{\varOmega _2}\left( {L,\varphi ,{\lambda _{JS1}},{\lambda _{JS2}},{\lambda _{JE}}} \right) \end{aligned}$$
(78)

By substituting (78) into (59.1), we finish the proof.

Appendix 5: Proof of Lemma 3

By substituting (49), (50), (51), and (5) into (61), we obtain

$$\begin{aligned}&P_{out{\mathrm{,OPT}}}^{{\mathrm{STWJNC,1}}} = 1 - \Pr \left[ \begin{array}{l} {g_{S1{R_s}}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }},{g_{S2{R_s}}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }},\\ {g_{{R_s}S1}} \ge \frac{{\varphi - 1}}{{{\omega _4}\psi {g_{{J_s}{R_s}}}}},{g_{{R_s}S2}} \ge \frac{{\varphi - 1}}{{{\omega _4}\psi {g_{{J_s}{R_s}}}}} \end{array} \right] \nonumber \\&\quad = 1 - \int _{\frac{{\varphi - 1}}{{{\omega _1}\psi }}}^\infty {{f_{{g_{S1{R_s}}}}}\left( {{x_1}} \right) } \int _{\frac{{\varphi - 1}}{{{\omega _1}\psi }}}^\infty {{f_{{g_{S2{R_s}}}}}\left( {{x_2}} \right) } \int _0^\infty {{f_{{g_{{J_s}{R_s}}}}}\left( {{x_3}} \right) } \nonumber \\&\quad \int _{\frac{{\varphi - 1}}{{{\omega _4}\psi {x_3}}}}^\infty {{f_{{g_{{R_s}S1}}}}\left( {{x_4}} \right) } \int _{\frac{{\varphi - 1}}{{{\omega _4}\psi {x_3}}}}^\infty {{f_{{g_{{R_s}S2}}}}\left( {{x_5}} \right) } d{x_5}d{x_4}d{x_3}d{x_2}d{x_1} \end{aligned}$$
(79)

From the optimal jammer and relay selection strategy, in (48a), the CDF of RV \({g_{{J_s}{R_s}}}\) is expressed as

$$\begin{aligned} {F_{{g_{{J_s}{R_s}}}}}\left( {{x_3}} \right) = \Pr \left[ {\mathop {\mathop {\max }\limits _{\scriptstyle \,k = 1,2,\ldots ,K}}\limits _{\, m= 1,2,\ldots ,M} } \left( {{g_{ {J_k} {R_m}}}} \right) < {x_3} \right] = {\left( {1 - {e^{ - {\lambda _{JR}}{x_3}}}} \right) ^{KM}} \end{aligned}$$
(80)

By substituting (80), \({f_{{g_{S1{R_s}}}}}( {{x_1}} ) = {\lambda _{S1R}}{e^{ - {\lambda _{S1R}}{x_1}}}\), \({f_{{g_{S2{R_s}}}}}\left( {{x_2}} \right) = {\lambda _{S2R}}{e^{ - {\lambda _{S2R}}{x_2}}}\), \({f_{{g_{{J_s}{R_s}}}}}\left( {{x_3}} \right) = KM{\lambda _{JR}}\sum \nolimits _{k = 0}^{KM - 1} {C_{KM - 1}^k{{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{JR}}{x_3}}}}\), \({f_{{g_{{R_s}S1}}}}\left( {{x_4}} \right) = {\lambda _{RS1}}{e^{ - {\lambda _{RS1}}{x_4}}}\), and \({f_{{g_{{R_s}S2}}}}\left( {{x_5}} \right) = {\lambda _{RS2}}{e^{ - {\lambda _{RS2}}{x_5}}}\) into (79), we can obtain

$$\begin{aligned} P_{out{\mathrm{,opt}}}^{{\mathrm{STWJNC,1}}}& = 1 - {e^{\frac{{ - \left( {\varphi - 1} \right) \left( {{\lambda _{S1R}} + {\lambda _{S2R}}} \right) }}{{{\omega _1}\psi }}}}\nonumber \\&\quad \int _0^\infty {KM{\lambda _{JR}} \sum \limits _{k = 0}^{KM - 1} {C_{KM - 1}^k{{\left( { - 1} \right) }^k}{e^{ - \left( {1 + k} \right) {\lambda _{JR}}{x_3}}}{e^{\frac{{ - \left( {\varphi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}{{{\omega _4}\psi {x_3}}}}}} } d{x_3} \end{aligned}$$
(81)

From [32, Eq. (3.381.1)], \(\int _0^\infty {{e^{ - \beta /4x - \gamma x}}dx} = \sqrt{\beta /\gamma } {K_1}\left( {\sqrt{\beta \gamma } } \right)\), we obtain

$$\begin{aligned}&\int _0^\infty {{e^{ - \left( {1 + k} \right) {\lambda _{JR}}{x_3}}}{e^{\frac{{ - \left( {\varphi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}{{{\omega _4}\psi {x_3}}}}}} d{x_3} = \sqrt{\frac{{4\left( {\varphi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) }}{{\left( {1 + k} \right) {\omega _4}\psi {\lambda _{JR}}}}} \nonumber \\&\quad {K_1}\left( {\sqrt{\frac{{4\left( {1 + k} \right) \left( {\varphi - 1} \right) \left( {{\lambda _{RS1}} + {\lambda _{RS2}}} \right) {\lambda _{JR}}}}{{{\omega _4}\psi }}} } \right) \end{aligned}$$
(82)

By substituting (82) into (81), we complete the proof.

Appendix 6: Proof of Lemma 4

By substituting (54), (55), (56), and (57) into (62), we obtain

$$\begin{aligned} P_{out{\mathrm{,opt}}}^{{\mathrm{S T W J NC,2}}}& = 1 - \Pr \left[ \begin{array}{l} {g_{S1{R_s}}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {g_{S1E\max }},{g_{S2{R_s}}} \ge \frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {g_{S2E\max }},\\ {g_{{R_s}S 1}} \ge \frac{{\varphi - 1}}{{{\omega _4}\psi {g_{{J_s}{R_s}}}}} + \varphi {g_{{R_s} E \max }},{g_{{R_s}S 2}} \ge \frac{{\varphi - 1}}{{{\omega _4}\psi {g_{{J_s}{R_s}}}}} + \varphi {g_{{R_s} E \max }} \end{array} \right] \nonumber \\& = 1 - \int _0^\infty {{f_{{g_{S1 E \max }}}} \left( {{x_1}} \right) \int _0^\infty {{f_{{g_{S2E \max }}}} \left( {{x_2}} \right) } \int _{\frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {x_1}}^\infty {{f_{{g_{S1{R_s}}}}} \left( {{x_3}} \right) \int _{\frac{{\varphi - 1}}{{{\omega _1}\psi }} + \varphi {x_2}}^\infty {{f_{{g_{S2{R_s}}}}} \left( {{x_4}} \right) } } } \nonumber \\&\quad \int _0^\infty {{f_{{g_{{J_s}{R_s}}}}} \left( {{x_5}} \right) \int _0^\infty {{f_{{g_{{R_s}E \max }}}} \left( {{x_6}} \right) \int _{\frac{{\varphi - 1}}{{{\omega _4}\psi {x_5}}} + \varphi {x_6}}^\infty {{f_{{g_{{R_s}S1}}}} \left( {{x_7}} \right) \int _{\frac{{\varphi - 1}}{{{\omega _4}\psi {x_5}}} + \varphi {x_6}}^\infty {{f_{{g_{{R_s} S 2}}}} \left( {{x_8}} \right) } } } } \nonumber \\&\quad {d{x_8}d{x_7}d{x_6}d{x_5}d{x_4}d{x_3}d{x_2}d{x_1}} \end{aligned}$$
(83)

By substituting the PDFs of the eight RVs \({{g_{S1E\max }}}\), \({S2E\max }\), \({S1{R_s}}\), \({S2{R_s}}\), \({{g_{{J_s}{R_s}}}}\), \({{g_{{R_s}E\max }}}\), \({{g_{{R_s}S1}}}\), and \({{g_{{R_s}S2}}}\), into (83) and after some manipulations of (83), the Eq. (64) in Lemma 4 is obtained. This completes the proof.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, S.Q., Kong, H.Y. Improving Secrecy Outage and Throughput Performance in Two-Way Energy-Constraint Relaying Networks Under Physical Layer Security. Wireless Pers Commun 96, 6425–6457 (2017). https://doi.org/10.1007/s11277-017-4485-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-017-4485-8

Keywords

Search

Navigation