Performance Analysis of Cooperative Spectrum Sensing Network Using Optimization Technique in Different Fading Channels

Abstract

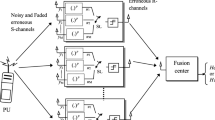
Spectrum sensing is an important task to find out the spectrum holes in a given radio spectrum. Spectrum sensing performance is improved with the aid of multiple cognitive radios (CRs) in the network and each CR having multiple antennas in different fading channels (Rayleigh, Hoyt and Weibull fading channel). In this paper, we have considered that each CR having multiple antennas and improved energy detector (IED) scheme is used for detection of primary user. Imperfect channel is considered between CRs and fusion center (i.e. in reporting channel) with an error probability rate (r). We have derived the novel expression for missed detection probability (P _m ), closed form of expression to find out optimal value of number of CR users (N _opt ), closed form of expression and procedure to find an optimal value of normalized threshold value (λ _n,opt ), expression for optimal value of arbitrary power of received signal (P _opt ) and calculation of minimum value of total error in different fading channels are provided. Performance is evaluated to find out (N _opt ), (λ _n,opt ), (P _opt ) and to calculate minimum error value for various network parameters like SNR, r, λ _n and multiple number of antennas (M). It is observed that detection performance is improved by using multiple antennas at each CR. Comparison between conventional energy detector and IED, comparison among Rayleigh, Hoyt and Weibull fading channels also provided for different cases of network parameters.

Appendices

Appendix 1

1.1 Missed Detection Probability $(P_{m} )$ in Rayleigh Fading Channel

Probability density function for Rayleigh fading channel when the signal is present is given in [10] as:

$$f_{{y_{i} |H_{1} }} (y) = \frac{{2y^{{\frac{2 - p}{p}}} }}{{p(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}\exp \left( { - \frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} }}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right)$$

(23)

Missed detection probability can be calculated for Rayleigh fading channel as [9]

$$P_{m} = pr(y < \lambda |H_{1} ) = \int_{0}^{\lambda } {f_{{w_{i} |H_{1} }} } (y)dy$$

(24)

$$= \int_{0}^{\lambda } {\frac{{2y^{{\frac{2 - p}{p}}} }}{{p(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}\exp \left( { - \frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} }}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right)} dy$$

(25)

$$= \int_{0}^{{\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} }}{{E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} }}}} {\exp \left( { - t} \right)dt}$$

(26)

$$P_{m} = \left( {1 - \exp \left( {{{ - \lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} } \mathord{\left/ {\vphantom {{ - \lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} } {(1 + \gamma )\sigma_{n}^{2} }}} \right. \kern-0pt} {(1 + \gamma )\sigma_{n}^{2} }}} \right)} \right)$$

(27)

where $\gamma = {\raise0.7ex\hbox{${E_{s} \sigma_{h}^{2} }$} \!\mathord{\left/ {\vphantom {{E_{s} \sigma_{h}^{2} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}$ is sensing channel SNR.

We have considered that each CR is having multiple antennas and selection combining (SC) scheme is used to select the maximum value of antenna among all antennas (M).

Using SC diversity scheme maximum value from all branches can be calculated as described in [10]

$$Z = \Pr [\hbox{max} (W_{1} ,W_{2} ,W_{3} \ldots W_{M} )]$$

(28)

Under hypothesis $H_{1}$: using SC diversity scheme missed detection probability can be calculated as:

$$P_{m} = pr[max(W_{1} ,W_{2} ,W_{3} \ldots_{M} ) \le \;|H_{1} ]$$

(29)

Having multiple antennas and using SC diversity scheme at each CR, expression for $P_{m}$ in Rayleigh fading channel is:

$$P_{m} = \left( {1 - \exp \left( {{{ - \lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} } \mathord{\left/ {\vphantom {{ - \lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} } {(1 + \gamma )\sigma_{n}^{2} }}} \right. \kern-0pt} {(1 + \gamma )\sigma_{n}^{2} }}} \right)} \right)^{M}$$

(30)

1.2 Missed Detection Probability $(P_{m} )$ in Hoyt Fading Channel

Probability density function for Hoyt fading channel when the signal is present is given in [11] as:

$$f_{{y_{i} |H_{1} }} (y) = \frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}} - 1}} }}{{p\sigma_{1} \sigma_{2} }}\exp \left( { - \left( {\frac{{y^{2/p} }}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} + \frac{1}{{\sigma_{1}^{2} }}} \right)} \right)I_{0} \left( {\left( {\frac{{y^{2/p} }}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} - \frac{1}{{\sigma_{1}^{2} }}} \right)} \right)$$

(31)

where $\sigma_{1}^{2} = \frac{{E_{s} \sigma_{I}^{2} + \sigma_{n}^{2} }}{2}$ and $\sigma_{2}^{2} = \frac{{E_{s} \sigma_{q}^{2} + \sigma_{n}^{2} }}{2}$. $\sigma_{I} = \sqrt {\frac{{\varOmega q^{2} }}{{1 + q^{2} }}}$, $\sigma_{q} = \sqrt {\frac{\varOmega }{{1 + q^{2} }}}$ and ‘q’ is the Hoyt fading parameter that ranges from 0 to 1.

Missed detection probability can be calculated for Hoyt fading channel as [11]

$$P_{m} = pr(y < \lambda |H_{1} ) = \int_{0}^{\lambda } {f_{{w_{i} |H_{1} }} } (y)dy$$

(32)

$$= \int\limits_{0}^{\lambda } {\frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}} - 1}} }}{{p\sigma_{1} \sigma_{2} }}\exp \left( { - \left( {\frac{{y^{2/p} }}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} + \frac{1}{{\sigma_{1}^{2} }}} \right)} \right)I_{0} \left( {\left( {\frac{{y^{2/p} }}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} - \frac{1}{{\sigma_{1}^{2} }}} \right)} \right)} dy$$

(33)

Missed detection probability can be calculated from CDF of Hoyt fading channel, it is given in [11], as

$$F_{{Z|H_{1} }} (z) = \frac{1}{16}\left[ {1 + \exp ( - Az^{2/p} )I_{0} (Bz^{2/p} ) - 2Q(u_{1} ,v_{1} )} \right]$$

(34)

where $A = {\kern 1pt} \,\left( {\frac{1}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} + \frac{1}{{\sigma_{1}^{2} }}} \right)$, $B = {\kern 1pt} \,\left( {\frac{1}{4}} \right)\left( {\frac{1}{{\sigma_{2}^{2} }} - \frac{1}{{\sigma_{1}^{2} }}} \right)$ and $u_{1} = \sqrt {\left( {A - \sqrt {A^{2} - B}^{2} } \right)z^{2/p} }$,

$$V_{1} = \sqrt {\left( {A + \sqrt {A^{2} - B}^{2} } \right)z^{2/p} }$$

Having multiple antennas and using SC diversity scheme at each CR, expression for $P_{m}$ in Hoyt fading channel is:

$$P_{m} = \frac{1}{16}\left[ {1 + \exp ( - Az^{2/p} )I_{0} (Bz^{2/p} ) - 2Q(u_{1} ,v_{1} )} \right]^{M}$$

(35)

1.3 Missed Detection Probability $(P_{m} )$ in Weibull Fading Channel

Probability density function for Weibull fading channel when the signal is present is given in [17] as:

$$f_{{w_{i} |H_{1} }} (y) = \frac{{2y^{{\left( {2/p} \right) - 1}} C}}{p}\left[ {\frac{\varGamma (P)}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right]\left( {y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} } \right)^{C - 1} \exp \left( { - \left\{ {\frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right\}^{C} } \right)$$

(36)

Where $C = {\raise0.7ex\hbox{$V$} \!\mathord{\left/ {\vphantom {V 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}$ and $P = 1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 C}}\right.\kern-0pt} \!\lower0.7ex\hbox{$C$}}$ V – is Weibull fading parameter.

Missed detection probability can be calculated for Weibull fading channel as [9]

$$P_{m} = pr(y < \lambda |H_{1} ) = \int_{0}^{\lambda } {f_{{w_{i} |H_{1} }} } (y)dy$$

(37)

$$= \int_{0}^{\lambda } { \frac{{2y^{{\left( {2/p} \right) - 1}} C}}{p}\left[ {\frac{\varGamma (P)}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right]\left( {y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} } \right)^{C - 1} \exp \left( { - \left\{ {\frac{{y^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right\}^{C} } \right)dy}$$

(38)

$$= \int_{0}^{{\left( {\frac{{\varGamma (P)\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} }}{{(E_{s} \sigma_{h}^{2} + \sigma_{n}^{2} )}}} \right)}} {\exp ( - t)dt}$$

(39)

$$P_{m} = \left[ {1 - \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C} } \right)} \right]$$

(40)

where $\gamma = {\raise0.7ex\hbox{${E_{s} \sigma_{h}^{2} }$} \!\mathord{\left/ {\vphantom {{E_{s} \sigma_{h}^{2} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}$ is sensing channel SNR, $C = {\raise0.7ex\hbox{$V$} \!\mathord{\left/ {\vphantom {V 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}$ and $P = 1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 C}}\right.\kern-0pt} \!\lower0.7ex\hbox{$C$}}$.

In above expression, if we substitute V = 2 in (40), it is similar to (27). It refers that if Weibull fading parameter value becomes (V = 2), then that distribution becomes to Rayleigh distribution.

Having multiple antennas and using SC diversity scheme at each CR, expression for $P_{m}$ in Weibull fading channel is:

$$P_{m} = \left[ {1 - \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 P}}\right.\kern-0pt} \!\lower0.7ex\hbox{$P$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C} } \right)} \right]^{M}$$

(41)

Appendix 2

2.1 Optimization of Normalized Threshold Value $(\lambda_{n,opt} )$ in Rayleigh Fading Channel

To find out optimal value of normalized threshold

$$\begin{aligned} \frac{\partial Z(n)}{{\partial \lambda_{n} }} = - N(2r - 1)\left[ {(1 - P_{f} )(1 - r) + rP_{f} } \right]^{N - 1} \frac{{\partial P_{f} }}{{\partial \lambda_{n} }} \hfill \\ \, + N(1 - 2r)\left[ {P_{m} (1 - r) + r(1 - P_{m} )} \right]^{N - 1} \frac{{\partial P_{m} }}{{\partial \lambda_{n} }} \hfill \\ \end{aligned}$$

(42)

For single antenna at each CR in the network;

$$\frac{{\partial P_{f} }}{{\partial \lambda _{n} }} = - M\frac{{2\lambda ^{{(2 - p)/p}} }}{p}\left[ {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda ^{{2/p}} }$} \!\mathord{\left/ {\vphantom {{\lambda ^{{2/p}} } {\sigma _{n}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma _{n}^{2} }$}}} \right)} \right]^{{M - 1}} \exp \left( { - \frac{{\lambda ^{{2/p}} }}{{\sigma _{n}^{2} }}} \right)$$

(43)

$$\frac{{\partial P_{m} }}{{\partial \lambda _{n} }} = M\frac{{2\lambda ^{{(2 - p)/p}} }}{{p\left( {1 + \gamma } \right)}}\left[ {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda ^{{2/p}} }$} \!\mathord{\left/ {\vphantom {{\lambda ^{{2/p}} } {\sigma _{n}^{2} \left( {1 + \gamma } \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma _{n}^{2} \left( {1 + \gamma } \right)}$}}} \right)} \right]^{{M - 1}} \exp \left( { - \frac{{\lambda ^{{2/p}} }}{{\sigma _{n}^{2} \left( {1 + \gamma } \right)}}} \right)$$

(44)

Case (i) For M = 1, N = 1, q = 0.1, and p = 2 represent the single antenna with CED, $(\lambda_{n,opt} )$ value is:

$$\lambda_{n,opt} = \frac{{\ln \left( {1 + \gamma } \right)}}{{\left( {{\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma {1 + \gamma }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1 + \gamma }$}}} \right)}}$$

(45)

Case (ii) For M = 1, N = 1, q = 0.1, and p = 3 represent the single antenna with IED, $(\lambda_{n,opt} )$ value is:

$$\lambda_{n,opt} = \left[ {\frac{{\ln \left( {1 + \gamma } \right)}}{{\left( {{\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma {1 + \gamma }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1 + \gamma }$}}} \right)}}} \right]^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(46)

Case (iii) For M = 1, N = 1, q = 0.1, and p = 4 represent the single antenna with IED, $(\lambda_{n,opt} )$ value is:

$$\lambda_{n,opt} = \left[ {\frac{{\ln \left( {1 + \gamma } \right)}}{{\left( {{\raise0.7ex\hbox{$\gamma $} \!\mathord{\left/ {\vphantom {\gamma {1 + \gamma }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${1 + \gamma }$}}} \right)}}} \right]^{2}$$

(47)

2.2 Optimization of Normalized Threshold Value $(\lambda_{n,opt} )$ in Hoyt Fading Channel

To find out optimal value of normalized threshold

$$\begin{aligned} \frac{\partial Z(n)}{{\partial \lambda_{n} }} = - N(2r - 1)\left[ {(1 - P_{f} )(1 - r) + rP_{f} } \right]^{N - 1} \frac{{\partial P_{f} }}{{\partial \lambda_{n} }} \hfill \\ \, + N(1 - 2r)\left[ {P_{m} (1 - r) + r(1 - P_{m} )} \right]^{N - 1} \frac{{\partial P_{m} }}{{\partial \lambda_{n} }} \hfill \\ \end{aligned}$$

(48)

For single antenna at each CR in the network;

$$\frac{{\partial P_{f} }}{{\partial \lambda _{n} }} = - M\frac{{2\lambda ^{{2 - {\text{p/}}p}} }}{p}\left[ {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda ^{{2/p}} }$} \!\mathord{\left/ {\vphantom {{\lambda ^{{2/p}} } {\sigma _{n}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma _{n}^{2} }$}}} \right)} \right]^{{M - 1}} \exp \left( { - \frac{{\lambda ^{{2/p}} }}{{\sigma _{n}^{2} }}} \right)$$

(49)

$$\frac{{\partial P_{m} }}{{\partial \lambda_{n} }} = \frac{\partial }{{\partial \lambda_{n} }}\left[ {\frac{1}{16}\left[ {1 + \exp ( - Az^{2/p} )I_{0} (Bz^{2/p} ) - 2Q(u_{1} ,v_{1} )} \right]^{M} } \right]$$

(50)

Where $\gamma = {{E_{s} \sigma_{h}^{2} } \mathord{\left/ {\vphantom {{E_{s} \sigma_{h}^{2} } {\sigma_{n}^{2} }}} \right. \kern-0pt} {\sigma_{n}^{2} }}$ is sensing channel SNR.

2.3 Optimization of Normalized Threshold Value $(\lambda_{n,opt} )$ in Weibull Fading Channel

To find out optimal value of normalized threshold

$$\begin{aligned} \frac{\partial Z(n)}{{\partial \lambda_{n} }} = - N(2r - 1)\left[ {(1 - P_{f} )(1 - r) + rP_{f} } \right]^{N - 1} \frac{{\partial P_{f} }}{{\partial \lambda_{n} }} \hfill \\ \, + N(1 - 2r)\left[ {P_{m} (1 - r) + r(1 - P_{m} )} \right]^{N - 1} \frac{{\partial P_{m} }}{{\partial \lambda_{n} }} \hfill \\ \end{aligned}$$

(51)

For single antenna at each CR in the network;

$$\frac{{\partial P_{f} }}{{\partial \lambda _{n} }} = - M\frac{{2\lambda ^{{{{(2 - p)} \mathord{\left/ {\vphantom {{(2 - p)} p}} \right. \kern-\nulldelimiterspace} p}}} }}{p}\left[ {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda ^{{2/p}} }$} \!\mathord{\left/ {\vphantom {{\lambda ^{{2/p}} } {\sigma _{n}^{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma _{n}^{2} }$}}} \right)} \right]^{{M - 1}} \exp \left( { - \frac{{\lambda ^{{2/p}} }}{{\sigma _{n}^{2} }}} \right)$$

(52)

$$\frac{{\partial P_{m} }}{\partial \lambda } = M\left[ {1 - \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + )}}} \right\}^{C} } \right)} \right]^{M - 1} \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C} } \right)C\left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C - 1} \frac{2}{p}\frac{{\lambda^{{\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}} \right) - 1}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}$$

(53)

Substituting N = 1, M = 1, q = 0.1 and (52), (53) in (51), then equating to zero we get an equation for optimal value normalized threshold value in the form of;

$$\lambda_{n,opt} = \left[ {\left\{ {\frac{{C\ln \left( {1 + \gamma } \right)}}{{\left[ {1 - \left( {\frac{1}{1 + \gamma }} \right)^{C} } \right]}}\left( {\frac{1}{{\varGamma (1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 C}}\right.\kern-0pt} \!\lower0.7ex\hbox{$C$}})}}} \right)} \right\}^{{\frac{1}{C}}} } \right]^{{{\raise0.7ex\hbox{$P$} \!\mathord{\left/ {\vphantom {P 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(54)

Appendix 3

3.1 Optimization of Arbitrary Power of Received Signal Value $(P_{opt} )$ in Rayleigh Fading Channel

To find out optimal value of arbitrary power of received signal

$$\begin{aligned} \frac{\partial Z(n)}{\partial p} = - N(2r - 1)\left[ {(1 - P_{f} )(1 - r) + rP_{f} } \right]^{N - 1} \frac{{\partial P_{f} }}{\partial p} \hfill \\ \, + N(1 - 2r)\left[ {P_{m} (1 - r) + r(1 - P_{m} )} \right]^{N - 1} \frac{{\partial P_{m} }}{\partial p} \hfill \\ \end{aligned}$$

(55)

For single antenna at each CR in the network;

$$\frac{{\partial P_{f} }}{\partial p} = - \frac{{2\lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} }}{{p^{2} \sigma_{n}^{2} }}ln\lambda M\left( {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} }$} \!\mathord{\left/ {\vphantom {{\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}} \right)} \right)^{M - 1} \exp \left( { - {\raise0.7ex\hbox{${\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} }$} \!\mathord{\left/ {\vphantom {{\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}} \right)$$

(56)

$$\frac{{\partial P_{m} }}{{\partial \lambda_{n} }} = - \frac{2M\log \lambda }{{p^{2} }}\left( {\frac{{\lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} }}{{2(1 + \gamma )\sigma_{n}^{2} }}} \right)\exp \left( { - \frac{{\lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} }}{{(1 + \gamma )\sigma_{n}^{2} }}} \right)\left[ {1 - \exp \left( { - \frac{{\lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} }}{{(1 + \gamma )\sigma_{n}^{2} }}} \right)} \right]^{M - 1}$$

(57)

where $\gamma = {{E_{s} \sigma_{h}^{2} } \mathord{\left/ {\vphantom {{E_{s} \sigma_{h}^{2} } {\sigma_{n}^{2} }}} \right. \kern-0pt} {\sigma_{n}^{2} }}$ is sensing channel SNR.

Substituting N = 1, M = 1 and (56), (57) in (55) results in

$$p_{opt} = \frac{2\log \lambda }{{\log \left[ {\left( {\frac{{\log (1 + \gamma )\sigma_{n}^{2} }}{{\left[ {1 - \frac{1}{(1 + \gamma )}} \right]}}} \right)} \right]}}$$

(58)

Substituting N = 2, M = 1 and (56), (57) in (55) results in

$$c_{1} x - c_{3} = \ln \left[ {\frac{{1 - 0.889\exp \left( { - c_{2} x^{2} } \right) + 0.889\exp \left( { - c_{2} x} \right)}}{1 - 0.889\exp ( - x)}} \right]$$

(59)

where$x = \lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}}$ $C_{1} = \left( {1 + \frac{1}{1 + \gamma }} \right)$ $C_{2} = \left( {\frac{1}{1 + \gamma }} \right)$ $C_{3} = \ln (C_{2} )$Finally, expression for optimal value of arbitrary power of received signal is:

$$p_{opt} = \ln (\lambda^{2} - x)$$

(60)

3.2 Optimization of Arbitrary Power of Received Signal Value $(P_{opt} )$ in Weibull Fading Channel

To find out optimal value of arbitrary power of received signal

$$\begin{aligned} \frac{\partial Z(n)}{\partial p} = - N(2r - 1)\left[ {(1 - P_{f} )(1 - r) + rP_{f} } \right]^{N - 1} \frac{{\partial P_{f} }}{\partial p} \hfill \\ \, + N(1 - 2r)\left[ {P_{m} (1 - r) + r(1 - P_{m} )} \right]^{N - 1} \frac{{\partial P_{m} }}{\partial p} \hfill \\ \end{aligned}$$

(61)

For single antenna at each CR in the network;

$$\frac{{\partial P_{f} }}{\partial p} = - \frac{{2\lambda^{{{2 \mathord{\left/ {\vphantom {2 p}} \right. \kern-0pt} p}}} }}{{p^{2} \sigma_{n}^{2} }}ln\lambda M\left( {1 - \exp \left( { - {\raise0.7ex\hbox{${\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} }$} \!\mathord{\left/ {\vphantom {{\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}} \right)} \right)^{M - 1} \exp \left( { - {\raise0.7ex\hbox{${\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} }$} \!\mathord{\left/ {\vphantom {{\lambda^{{{{(2} \mathord{\left/ {\vphantom {{(2} p}} \right. \kern-0pt} p})}} } {\sigma_{n}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sigma_{n}^{2} }$}}} \right)$$

(62)

$$\frac{{\partial P_{m} }}{\partial p} = - M\left[ {1 - \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C} } \right)} \right]^{M - 1} \exp \left( { - \left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C} } \right)C\left\{ {\frac{{\lambda^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}}} \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}} \right\}^{C - 1} \frac{2}{{p^{2} }}\frac{{\lambda^{{\left( {{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 p}}\right.\kern-0pt} \!\lower0.7ex\hbox{$p$}}} \right)}} \log \lambda \varGamma (P)}}{{\sigma_{n}^{2} (1 + \gamma )}}$$

(63)

where $\gamma = {{E_{s} \sigma_{h}^{2} } \mathord{\left/ {\vphantom {{E_{s} \sigma_{h}^{2} } {\sigma_{n}^{2} }}} \right. \kern-0pt} {\sigma_{n}^{2} }}$ is sensing channel SNR.Substituting N = 1, M = 1, q = 0.1 and (62), (63) in (61) results in

$$p_{opt} = \frac{2\ln \lambda }{{\ln \left\{ {\frac{{C\ln \left( {1 + \gamma } \right)}}{{\left[ {1 - \left( {\frac{1}{1 + \gamma }} \right)^{C} } \right]}}\left( {\frac{1}{{\varGamma (1 + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 V}}\right.\kern-0pt} \!\lower0.7ex\hbox{$V$}})}}} \right)} \right\}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 C}}\right.\kern-0pt} \!\lower0.7ex\hbox{$C$}}}} }}$$

(64)