Zadoff–Chu Sequence Based Timing Offset Estimation for OFDM Systems

Abstract

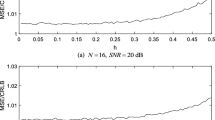
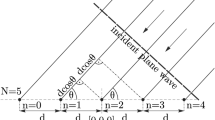
In this article, timing synchronization in OFDM is attained with the help of Zadoff–Chu sequence as a training symbol. An algorithm based on the cross-correlation property of fractional Fourier transform (FRFT) is proposed to generate a new timing metric. In this algorithm, cross correlation of received signal and Z–Chu sequence is taken at the receiver side in FRFT domain. The mathematical analysis of proposed estimator has been done and the variance of timing metric is obtained under the effect of AWGN channel. The simulation result shows that the variance of timing metric decreases as signal to noise ratio increases. The mean and MSE of the timing offset is simulated under HYPERLAN indoor channel (type-A). The proposed estimation method has been compared with existing methods and established as a better method to combat timing offset.

Appendix 1

From Sect. 5, the mean square error of the proposed timing metric is calculated in terms of $I_{1} , I_{2} , I_{3}$ and $I_{4}$ using formulae $Var(XY) = E(X)^{2} E(Y)^{2} - \left( {E(X)} \right)^{2} \left( {E(Y)} \right)^{2}$ as given in (13) where $I_{1}$ is considered as fourth moment of the received signal in FRFT domain denoted by (14). After expanding (14) into (15), the equation can be re-written as

$$= \underbrace {{E\left[ {\left| {\tilde{X}_{ \propto ,l} (u)} \right|^{4} } \right]}}_{A} + \underbrace {{E\left[ {\left| {W_{ \propto ,l} (u)} \right|^{4} } \right]}}_{B} + \underbrace {{6E\left[ {\left| {\tilde{X}_{ \propto ,l} (u)} \right|^{2} \left| {W_{ \propto ,l} (u)} \right|^{2} } \right]}}_{C}$$

(24)

where part A is the fourth moment of transmitted signal, part B is the fourth moment of AWGN noise and part C is the expectation of product of these two independent terms.

The fourth moment of transmitted signal can be calculated as follows

$$E\left[ {\left| {\tilde{X}_{ \propto } (u)} \right|^{4} } \right] = E\left\{ {\left| {aA_{ \propto } e^{{i2\pi K\left( {\tau \sin \propto } \right)^{2} }} e^{{i\tau^{2} \sin \propto \cos \propto /2}} } \right|^{4} } \right\}$$

(25)

The above equation can be written after calculating the value of $\tilde{X}_{ \propto } (u)$ as given below. According to the modulation property defined in FRFT, if a signal is delayed by τ, then its FRFT can be calculated as

$$\tilde{X}_{ \propto } (u) = B_{ \propto } X_{ \propto } (u - \tau \cos \propto )$$

(26)

where $B_{ \propto } = exp\left[ {{\text{i}}\tau^{2} \sin \propto \cos \propto /2 - {\text{i}}u\tau \sin \propto } \right]$ and $\tilde{X}_{ \propto } (u)$ is the FRFT of delayed signal. Using the formula for the calculation of FRFT given in [11], the above equation can be written as

$$\tilde{X}_{ \propto } (u) = B_{ \propto } A_{ \propto } \mathop \smallint \limits_{ - \infty }^{\infty } x(t)e^{{j\frac{{\left( {u - \tau cos \propto } \right)^{2} + t^{2} }}{2}\cot \propto }} e^{ - j(u - \tau \cos \propto )t\csc \propto } dt$$

(27)

where $A_{ \propto } = \sqrt {1/2\pi \sin \propto }$ and $x(t)$ is the transmitted chirp signal given in (1). After substituting the value of $x(t)$ in above equation, it can be re-written as

$$\tilde{X}_{ \propto } (u) = B_{ \propto } A_{ \propto } a\mathop \smallint \limits_{ - T/2}^{T/2} e^{{j\pi Kt^{2} }} e^{{j\frac{{\left( {u - \tau cos \propto } \right)^{2} + t^{2} }}{2}\cot \propto }} e^{ - j(u - \tau \cos \propto )t\csc \propto } dt$$

(28)

As given in Tao et al. [11], the magnitude of FRFT is concentrated maximally at $u = \tau \cos \propto$ according to (26). Thus using the relation given in (4), the above equation is reduced into following expression

$$\tilde{X}_{ \propto } (u) = B_{ \propto } A_{ \propto } aT$$

(29)

Substitute the value of $B_{ \propto }$ in above equation, we get

$$\tilde{X}_{ \propto } (u) = aA_{ \propto } Te^{{i2\pi K\left( {\tau \sin \propto } \right)^{2} }} e^{{i\tau^{2} \sin \propto \cos \propto /2}}$$

(30)

Assume unity time interval (T = 1)

$$\tilde{X}_{ \propto } (u) = aA_{ \propto } e^{{i2\pi K\left( {\tau \sin \propto } \right)^{2} }} e^{{i\tau^{2} \sin \propto \cos \propto /2}}$$

(31)

Substitute the value of $\tilde{X}_{ \propto } (u)$ in $E[|\tilde{X}_{ \propto } (u)|^{4} ]$, we can determine the fourth moment of transmitted delayed signal. Thus (25) reduces into following equation

$$E\left[ {\left| {\tilde{X}_{ \propto } (u)} \right|^{4} } \right] = a^{4} |A_{ \propto } |^{4}$$

(32)

In part B, the fourth moment of AWGN noise is calculated using formula $E[X^{P} ] = \sigma^{P} (P - 1)!!$ if p is even. For this we need to calculate the second moment of noise signal. After solving the second moment and some mathematical manipulation, the value of $E[|W_{ \propto } (u)|^{2} ]$ comes out to be [11]

$$E[|W_{ \propto } (u)|^{2} ] = |A_{ \propto } |^{2} \sigma_{0}^{2}$$

(33)

Using above equation, we can calculate the value of $E[|W_{ \propto } (u)|^{4} ]$ using given formula.

$$\begin{aligned} E[|W_{ \propto } (u)|^{2} ] = |A_{ \propto } |^{4} \sigma_{0}^{4} (4 - 1)!! \hfill \\ E[|W_{ \propto } (u)|^{2} ] = 3|A_{ \propto } |^{4} \sigma_{0}^{4} \hfill \\ \end{aligned}$$

(34)

Part C can be calculated by taking expectation of their individual terms as follows

$$6E\left[ {\left| {\tilde{X}_{ \propto } (u)} \right|^{2} |W_{ \propto } (u)|^{2} } \right] = 6*E\left[ {\left| {\tilde{X}_{ \propto } (u)} \right|^{2} } \right]*E[|W_{ \propto } (u)|^{2} ]$$

(35)

The value of $E[|\tilde{X}_{ \propto } (u)|^{2} ]$ can be calculated in the same way as in (32) and using (33), we can re-write the above equation as

$$6E\left[ {\left| {\tilde{X}_{ \propto } \left( u \right)} \right|^{2} \left| {W_{ \propto } \left( u \right)} \right|^{2} } \right] = 6*\left( {a^{2} \left| {A_{ \propto } } \right|^{2} } \right)*\left( {\left| {A_{ \propto } } \right|^{2} \sigma_{0}^{2} } \right)$$

(36)

Substitute (32), (33) and (36) into (24), we get

$$I_{1} = E[|R_{ \propto ,d} (u)|^{4} ] = a^{4} |A_{ \propto } |^{4} + 3|A_{ \propto } |^{4} \sigma_{0}^{4} + 6a^{4} |A_{ \propto } |^{4} \sigma_{0}^{2}$$

(37)

Similarly $I_{2}$ represents the fourth moment of transmitted signal and using (32), it can be expressed as

$$I_{2} = E[|X_{ \propto ,l} (u)|^{4} ] = a^{4} |A_{ \propto } |^{4}$$

(38)

$I_{3}$ represents the square of second moment of received signal and can be written as

$$I_{3} = \left( {E[|R_{ \propto ,d} (u)|^{2} ]} \right)^{2} = \left( {E\left\{ {\left[ {\tilde{X}_{ \propto } (u) + W_{ \propto } (u)} \right]^{2} } \right\}} \right)^{2}$$

(39)

Expanding (39) into following expression

$$= \left( {E\left[ {\left| {\tilde{X}_{ \propto ,l} \left( u \right)} \right|^{2} } \right] + E\left[ {\left| {W_{ \propto } \left( u \right)} \right|^{2} } \right]} \right)^{2}$$

(40)

Using (36), (40) further reduces into

$$\left( {a^{2} |A_{ \propto } |^{2} + |A_{ \propto } |^{2} \sigma_{0}^{2} } \right)^{2}$$

(41)

and $I_{4}$ represents the square of second moment of transmitted signal and it can be written as

$$I_{4} = \left( {E[|X_{ \propto ,d} (u)|^{2} ]} \right)^{2} = \left( {a^{2} |A_{ \propto } |^{2} } \right)^{2}$$

(42)