Robust LCMV Beamformer for Direction of Arrival Mismatch Without Beam Broadening

Abstract

In this work, we propose a new and efficient algorithm to mitigate the signal look direction error problem in adaptive beamforming without broadening the main beam. The algorithm exploits a reference lobe in the region of signal look direction error. This reference lobe is the main beam of the generalized sidelobe canceller when there is no direction of arrival mismatch for the desired signal. The desired pattern is forced to follow the reference beam in the region of signal look direction error by utilizing multiple additional constraints. Simulations are performed in MATLAB to check and test the validity of the proposed algorithm on the basis of different scenarios.

Appendix

1.1 Definition of Important Terminologies

• (a) Adaptive Beamforming Adaptive beamforming is a spatial filtering technique that utilizes array of sensors to receive (or transmit) the signal from desired direction and to cancel interferences from the direction of jammers. For this purpose, the weights of the sensors are controlled adaptively through a suitable adaptive beamforming algorithm.

• (b) DOA Mismatch There are situations when the actual and presumed directions of source signals are not same due to environmental conditions or imperfection in element placement. Since beamforming algorithms are applied along presumed directions and in case of direction of arrival (DOA) mismatch, the signal from actual direction is considered as interference and is degraded by traditional beamforming algorithms. This problem is known as Direction of Arrival Mismatch Problem or Signal Look Direction Error Problem.

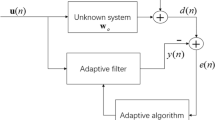
• (c) GSC Generalized side lobe canceller (GSC) is the alternate approach of LCMV beamformer. It has two branches as shown in block diagram of Fig. 2. In the fig., upper branch preserves the desired signal while lower branch is meant for interference cancellation.

• (d) LCMV Beamformer Linearly constrained minimum variance (LCMV) Beamformer is an adaptive beamforming technique to evaluate elemental weights by minimizing received signal output power while satisfying one or more linear equality constraints as given in expression (9) of the manuscript.

1.2 Derivation of ${\mathbf{w}}_{LC} = {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}}({\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}})^{ - 1} {\mathbf{f}}$

Equations (9) and (10) of the manuscript are reproduced below

$$ \mathop {\hbox{min} }\limits_{{\mathbf{w}}} {\mathbf{w}}^{H} {\mathbf{R}}_{y} {\mathbf{w}}\,\,\,{\text{Subject}}\,\,{\text{to}}\,\,k\,\,{\text{linear}}\,\,{\text{constraints}}\,\,{\mathbf{C}}^{H} {\mathbf{w}} = {\mathbf{f}} $$

(9)

The constraint matrix ${\mathbf{C}}$ contains $k$ steering vectors and ${\mathbf{f}}$ is the gain vector corresponding to each steering vector contained in the matrix ${\mathbf{C}}$. The solution to this optimization problem comes out to be,

$$ {\mathbf{w}}_{LC} = {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}}({\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}})^{ - 1} {\mathbf{f}} $$

(10)

Derivation A ULA of $M$ elements has been considered. So ${\mathbf{R}}_{y}$ is $M \times M$ matrix. Let the $M \times k$ matrix ${\mathbf{C}} = [{\mathbf{a}}(\theta_{c1} ){\mathbf{a}}(\theta_{c2} ) \ldots {\mathbf{a}}(\theta_{ck} )]$ and ${\mathbf{f}} = [f_{1} f_{2} \ldots f_{k} ]^{T}$ are constraint matrix and gain vector respectively. The cost function for the optimization problem expressed in (9) is given as under

$$ J = {\mathbf{w}}^{H} {\mathbf{R}}_{y} {\mathbf{w}} + \lambda_{1} ({\mathbf{w}}^{H} {\mathbf{a}}(\theta_{c1} ) - f_{1} ) + \cdots + \lambda_{k} ({\mathbf{w}}^{H} {\mathbf{a}}(\theta_{ck} ) - f_{k} ) $$

(i)

The derivative of the cost function comes out to be

$$ \frac{\partial J}{{\partial {\mathbf{w}}^{H} }} = {\mathbf{R}}_{y} {\mathbf{w}} + \lambda_{1} {\mathbf{a}}(\theta_{c1} ) + \cdots + \lambda_{k} {\mathbf{a}}(\theta_{ck} ) = {\mathbf{R}}_{y} {\mathbf{w}} + {\mathbf{C\lambda }} $$

(ii)

In Eq. (ii), ${\varvec{\uplambda}} = [\lambda_{1} \lambda_{2} \cdots \lambda_{k} ]^{T}$ is the vector containing Lagrange multipliers $\lambda_{1} ,\lambda_{2} , \ldots ,\lambda_{k}$

For optimization of cost function, $\frac{\partial J}{{\partial {\mathbf{w}}^{H} }}$ should be equal to null vector i.e.

$$ {\mathbf{R}}_{y} {\mathbf{w}} + {\mathbf{C\lambda }} = {\mathbf{0}} $$

(iii)

$$ {\mathbf{w}} = - {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }} $$

(iv)

In order to find ${\varvec{\uplambda}}$, expression (iii) is multiplied by ${\mathbf{w}}^{H}$

$$ {\mathbf{w}}^{H} {\mathbf{R}}_{y} {\mathbf{w}} + {\mathbf{w}}^{H} {\mathbf{C\lambda }} = {\mathbf{0}} $$

(v)

$$ {\mathbf{w}}^{H} {\mathbf{R}}_{y} {\mathbf{w}} + {\mathbf{f}}^{H} {\varvec{\uplambda}} = {\mathbf{0}} $$

(vi)

Putting value of ${\mathbf{w}}$ from expression (iv) into (v)

$$ ( - {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }})^{H} {\mathbf{R}}_{y} ( - {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }}) + {\mathbf{f}}^{H} {\varvec{\uplambda}} = {\mathbf{0}} $$

(vii)

$$ ( - {\varvec{\uplambda}}^{H} {\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} ){\mathbf{R}}_{y} ( - {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }}) + {\mathbf{f}}^{H} {\varvec{\uplambda}} = {\mathbf{0}} $$

(viii)

$$ {\varvec{\uplambda}}^{H} {\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }} + {\mathbf{f}}^{H} {\varvec{\uplambda}} = {\mathbf{0}} $$

(ix)

$$ {\varvec{\uplambda}}^{H} {\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}} = - {\mathbf{f}}^{H} $$

(x)

$$ {\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C\lambda }} = - {\mathbf{f}} $$

(xi)

$$ {\varvec{\uplambda}} = - ({\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}})^{ - 1} {\mathbf{f}} $$

(xii)

Putting value of ${\varvec{\uplambda}}$ from expression (xii) into (iv)

$$ {\mathbf{w}} = {\mathbf{w}}_{LC} = {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}}({\mathbf{C}}^{H} {\mathbf{R}}_{y}^{ - 1} {\mathbf{C}})^{ - 1} {\mathbf{f}} $$

(xiii)

This is the optimized weight vector for LCMV beamformer as given in Eq. (10).