Abstract
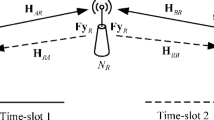
In this paper, a training scheme for multi-relay clustered wireless sensor networks is proposed for the destination cluster head node to estimate the individual source-relay and relay-destination channels. Compared with an existing training scheme, the proposed one has shown improved efficiency with reduced power and computation time in the training of the source relay channels. Furthermore, the training power allocation problem is analyzed. Based on minimizing the total mean-square-error (MSE) of all channel estimates, two approximate solutions for the power allocation among all network nodes and all training links are derived. The first solution is adaptive to the instantaneous relay-destination channel estimates, thus requires feedback from the destination during the training process. The other solution depends on channel variances only and has lower complexity in implementation. Simulation results demonstrate that the proposed training scheme and power allocation solutions obtain lower total MSE and higher network throughput than existing schemes.













Similar content being viewed by others
Notes
This model is an extremely special case of practical scenario and it is used for validating the proposed methods due to its yielding easier theoretical analysis. Subsequent simulations also demonstrate that the same conclusions drawn for this special case go to more practical one.
Due to the space limit, this BER performance of various training schemes over optimal PA are not given below. Besides, in the subsequent simulations, the regular schemes without considering training power allocation would be omitted for a more clear comparison.
References
Wang, D., & Jing, Y. (2015). Improved training and training power allocation schemes for multi-relay AF networks. In The 2015 14th Canadian workshop on information theory (CWIT), St. John’s, Newfoundland, Canada, July 6–9, pp. 200–203.
Nguyen, D. H. N., & Nguyen, H. H. (2011). Power allocation in wireless multiuser multi-relay networks with distributed beamforming. IET Communications, 5(14), 2040–2051.
Chen, D., Cong, J., Gurumani, S., et al. (2016). Platform choices and design demands for IoT platforms: Cost power, and performance tradeoffs. IET Cyber-Physical Systems: Theory and Applications, 1(1), 70–77.
Dohler, M., & Li, Y. (2010). Cooperative communications: hardware, channel and PHY. New Jersey, USA: Wiley.
Laneman, J. N., Tse, D. N. C., & Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50, 3062–3080.
Dong, Y., Hossain, M. J., & Cheng, J. (2016). Performance of wireless powered amplify and forward relaying over Nakagami-\(m\) fading channels with nonlinear energy harvester. IEEE Communications Letters, 20(4), 672–675.
Singh, K., Meng-Lin, K., & Lin, J.-C. (2016). Joint power allocation, equalization, and relay selection for MIMO relay networks with multipath receptions. IEEE Transactions on Vehicular Technology, 65(7), 5160–5174.
Wu, Y., Liu, W., & Li, K. (2017). Power allocation and relay selection for energy efficient cooperation in wireless sensor networks with energy harvesting. EURASIP Journal on Wireless Communications and Networking, 26, 1–11.
He, Z., Yang, J., Wang, X., et al. (2017). Channel estimation of MIMO relay systems with multiple relay nodes. IEEE Access, 5, 27649–27658.
Lioliou, P., Viberg, M., & Coldrey, M. (2012). Efficient channel estimation techniques for amplify and forward relaying systems. IEEE Transactions on Communications, 60(11), 3150–3155.
Tseng, F. S., Huang, W. J., & Wu, W. R. (2013). Robust far-end channel estimation in three-node amplify-and-forward MIMO relay systems. IEEE Transactions on Vehicular Technology, 62(8), 3752–3766.
Chiong, C. W. R., Rong, Y., & Xiang, Y. (2016). Blind channel estimation and signal retrieving for MIMO relay systems. Digital Signal Processing, 52, 35–44.
Wang, M., Li, C., & Huang, W. (2017). Semiblind channel estimation and precoding scheme in two-way multirelay networks. IEEE Transactions on Signal Processing, 65(10), 2576–2587.
Gao, F., Cui, T., & Nallanathan, A. (2008). On channel estimation and optimal training design for amplify and forward relay networks. IEEE Transactions on Wireless Communications, 7, 1907–1916.
Sun, S., & Jing, Y. (2011). Channel training design in amplify-and-forward mimo relay networks. IEEE Transactions on Wireless Communications, 10, 3380–3391.
Sun, S., & Jing, Y. (2012). Training and decodings for cooperative network with multiple relays and receive antennas. IEEE Transactions on Communications, 60(6), 1534–1544.
Li, X., Xing, C., Wu, Y. C., & Chan, S. C. (2010). Timing estimation and resynchronization for amplify-and-forward communication systems. IEEE Transactions on Signal Processing, 58(4), 2218–2229.
Huang, G., Wang, Y., & Coon, J. P., et al. (2012). Orthogonal training signal relaying for channel estimation in dual-hop AF relay networks. In IEEE Globecom-communication theory symposium, Anaheim, California, USA, December 3–7, pp. 2246–2250.
Zhang, S., Gao, F., Pei, C., & He, X. (2013). Segment training based individual channel estimation in one-way relay network with power allocation. IEEE Transactions on Wireless Communications, 12, 1300–1309.
Gao, Y., Lin, D., Li, B., & Li, S. (2010). Optimal training power allocation for amplify and forward relay networks. In International conference on communications, circuits and systems, pp. 73–77.
Wu, C., & Jing, Y. (2013). Power allocation in training for amplify-and-forward relay network. In IEEE vehicular technology conference (VTC).
Wu, C., Wang, D., & Jing, Y. (2014). MSE and outage probability based training power allocations for relay networks. IEEE Transactions on Communications, 62(7), 2260–2270.
Chakrabarti, A., Baynast, A., Sabharwal, A., et al. (2007). Low density parity check codes for the relay channel. IEEE Journal on Selected Areas in Communications, 25(2), 280–291.
Boyd, S., & Vandenberghe, L. (2004). Convex optimization. Cambridge: Cambridge University Press.
Ling, X., Wu, B., Ho, P., et al. (2012). Fast water-filling for agile power allocation in multi-channel wireless communications. IEEE Communications Letters, 16(8), 1212–1215.
Hui, H., Zhu, S., & LV, G. (2009). Power allocation for amplify-and-forward opportunistic relaying systems. IEICE Transactions on Communications, E92–B(11), 3541–3545.
Zhuo, W., & Yang, H. (2011). Power allocation of cooperative amplify-and-forward communications with multiple relays. The Journal of China University of Posts and Telecommunications, 4, 65–69.
Hassibi, B., & Hochwald, B. M. (2003). How much training is needed in multiple-antenna wireless links? IEEE Transactions on Information Theory, 49(4), 951–963.
Jing, Y., & Jafarkhani, H. (2009). Single and multiple relay selection schemes and their achievable diversity orders. IEEE Transactions on Wireless Communications, 8, 1414–1423.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This work has been presented in part at the Canadian Workshop on Information Theory, St. John’s, Canada, July 2015 [1].
This work was partly supported by the project of Natural Science and Engineering Research Council, Canada.
Appendices
Appendix 1: Proof of Lemma 1
Define
and
We will show that the defined \({\tilde{\gamma }}^*\) and \(\theta _i^*\)’s are the solutions to (22). This is equivalent to showing that \(\tilde{\theta }_i^*\in (0,1)\) and \(\sum _{i=1}^N\tilde{\theta }_i^*=1\). From the definitions of \(\tilde{\theta }_i^*\) and \(\tilde{\gamma }^*\) in (36) and (35), it is obvious that \(\sum _{i=1}^N\tilde{\theta }_i^*=1\). Next, we show that for \(i=1,\ldots ,N\), \(\tilde{\theta }_i^*\in (0,1)\). Define the following functions:
Obviously, \(\phi _i\) is a monotonically decreasing function of x. For \(x\in [0,1]\), by evaluating \(\phi _i(x)\) at \(x=1\) and \(x=0\), the minimum and maximum values of \(\phi _i(x)\) are achieved as follows
From the definition in (36), we have \({\tilde{\gamma }}^*=\phi _i({\tilde{\theta }}_i^*)\). Since \(\phi _i(x)\) is a continuous function, it is sufficient to show that \({\tilde{\theta }}_i^*\in (0,1)\) by showing that \({\tilde{\gamma }}^*\in (\phi _{i,\min },\phi _{i,\max })\) for \(i=1,\ldots ,N\). By using (14) and (20) in (35),
With the high SNR assumption, we have \(P_{f_i}\sigma _{g_i}^2\gg 1\). Thus \(P_{f_i}\gg \sigma _{g_i}^{-2}\) and
from which we can obtain that \(P_f^{-1}\sum _{i= 1}^N \sigma _{g_i}^{-2} \ll 1\). Thus from (40),
Since \(\sigma _{f_i},\sigma _{g_i}>0\), we have \(\tilde{\gamma }^*>\phi _{i,\min }\). Next, we show that \(\tilde{\gamma }^*<\phi _{i,\max }\). From (1), we have
where the inequality (a) is because \(\mu _i\in (0,1)\). Thus, when \(P_f>N(1-\mu _a)/(4\mu _a)\), we have
In these derivations, the inequality (b) is because \(0<\mu _a \le \mu _i<1\) and the inequality (c) is due to the inequality (a). We have shown \({\tilde{\gamma }}^*\in (\phi _{i,\min },\phi _{i,\max })\) for \(i=1,\ldots ,N\). Finally, (24) is shown for the proof by using (20), (21), and (42) in (22).
Appendix 2: Proof of Lemma 2
For homogeneous relay networks, we have \(\sigma _{f_i}^2=\sigma _f^2\) and \(\sigma _{g_i}^2=\sigma _g^2\), \(i=1, \ldots , N\). By using (1), after some tedious but straightforward calculations, the threshold of \({\tilde{P}}_t\) in (33) can be replaced with
where the function \({\tilde{P}}_t(\mu )\) is decreasing for \(\mu\) in the interval \(\left[ \mu _a,\mu _b \right]\). To prove this, let \(\alpha = \sqrt{\mu ^2+(1-\mu )^2}\). since \(0\le \mu _a\le \mu \le \mu _b\le 1\), we have
Thus, the following two solutions to \(\mu\) can be obtained by
On substituting \(\mu _1\) and \(\mu _2\) into (43) and calculating the first-order derivatives with respect to \(\alpha\), respectively, we have
From (44), we have \(2\alpha ^2\ge \sqrt{2\alpha ^2-1}\) and \({{\partial {\tilde{P}_t}(\mu )|_{\mu =\mu _1} } /{\partial \alpha }} <0\). For \(N\ge 2\), \({{\partial {{\tilde{P}}_t}(\mu )|_{\mu =\mu _2} } / {\partial \alpha }} >0\). Thus, when \(1/2\le \alpha ^2\le 1\), \({\tilde{P}_t}(\mu )|_{\mu =\mu _1}\) is a decreasing function of \(\alpha\) while \({{\tilde{P}}_t}(\mu )|_{\mu =\mu _2}\) is an increasing function for \(\alpha\). Besides, we know from (45) that the \(\mu _1\)-value increases while the \(\mu _2\)-value decreases as the \(\alpha\)-value increases. Therefore, \({\tilde{P}}_t(\mu )\) is always a decreasing function for any \(\mu \in \left[ \mu _a,\mu _b\right]\).
Thus, when all the relays are closer to the destination, the less the threshold of total training power is. In other words, for \(\mu _i\)’s\(=\mu _a\), the total training power threshold of making \(P_f^*>0\) is maximum, while for \(\mu _i\)’s \(=\mu _b\), the total training power threshold of making \(P_f^*>0\) is minimum. Then, we have
Lemma 2 is proved.
Rights and permissions
About this article
Cite this article
Yang, L., Wang, D. & Zhao, Q. Training Power Allocation Based on MSE-Minimization for Multi-Relay Amplify-and-Forward Cooperation in Wireless Sensor Networks. Wireless Pers Commun 106, 593–619 (2019). https://doi.org/10.1007/s11277-019-06181-9
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-019-06181-9