Outage Performance Comparison of Dual-Hop Full Duplex Underlay Cognitive Relay Networks

Abstract

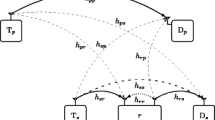
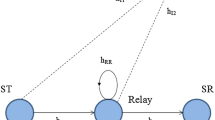
This paper investigates the outage probability performance of the secondary user (SU) in an underlay dual-hop, decode and forward (DF), full duplex cognitive relay network (FDCRN). First, we develop analytical closed form expression for outage probability and throughput for a dual-hop DF FDCRN by making use of the direct link signal as a useful signal to improve the signal-to-noise ratio at the secondary destination. Next, we compare the outage and throughput performance of various FDCRN and half duplex cognitive relay network (HDCRN) protocols, namely, (1) dual-hop DF FDCRN with direct link treated as interference, (2) dual-hop DF FDCRN with direct link signal cancelled by employing recursive backward interference cancellation technique, and (3) dual-hop DF HDCRN that employs maximal ratio combining at SD. Closed form expressions for the outage probabilities experienced in the secondary network are derived by taking into account the residual self-interference at the full duplex relay node, in independent non-identical Rayleigh fading channels. The analysis considers the maximum transmit power constraint of the individual secondary nodes and the tolerable interference threshold power constraint of the primary destination as well. The results demonstrate that the outage performance of the SU gets improved significantly when the direct link is exploited at the secondary destination. Further, we evaluate the impact of relay location and the power allocation ratio among secondary source and relay on the outage probability. The analytical results are validated by extensive Monte-Carlo simulations.

Appendices

Appendix

A Derivation of (10) and (11):

Let the random variables P and Q be defined as follows:

$P=min \left( P_{S,max},\frac{\zeta I_{th}}{ \vert h_{SP} \vert ^2} \right) \vert h_{SR} \vert ^2$

$Q=min \left( P_{R,max},\frac{(1-\zeta ) I_{th}}{ \vert h_{RP} \vert ^2} \right) \vert h_{RR} \vert ^2$.

First let us determine the CDF and PDF of P, which is useful for our derivation.

$$\begin{aligned} F_P(p)&=Pr \left( min \left( P_{S,max}, \frac{\zeta I_{th}}{ \vert h_{SP} \vert ^2} \right) \vert h_{SR} \vert ^2< p \right) \nonumber \\&=Pr \left( P_{S,max}\vert h_{SR} \vert ^2<p,P_{S,max}<\frac{\zeta I_{th}}{\vert h_{SP} \vert ^2} \right) \nonumber \\&\quad +\,Pr \left( \frac{\zeta I_{th}}{\vert h_{SP} \vert ^2}\vert h_{SR} \vert ^2 < p, P_{S,max} > \frac{\zeta I_{th}}{\vert h_{SP} \vert ^2} \right) \nonumber \\&=F_{\vert h_{SR} \vert ^2}\left( \frac{p}{P_{S,max}} \right) F_{\vert h_{SP} \vert ^2}\left( \frac{\zeta I_{th}}{P_{S,max}}\right) + \int _{\frac{\zeta I_{th}}{P_{S,max}}}^{\infty } F_{\vert h_{SR} \vert ^2}\left( \frac{py}{\zeta I_{th}} \right) f_{\vert h_{SP} \vert ^2}(y)dy \nonumber \\&=\left( 1-e^{-\frac{\zeta I_{th}}{P_{S,max} \lambda _{SP}}}\right) \left( 1-e^{-\frac{p}{P_{S,max} \lambda _{SR}}}\right) + \int _{\frac{\zeta I_{th}}{P_{S,max}}}^{\infty } \big (1-e^{-\frac{py}{\zeta I_{th} \lambda _{SR}}}\big ) \frac{e^{-y/\lambda _{SP}}}{\lambda _{SP}}dy \nonumber \\&=1-e^{-\frac{p}{P_{S,max} \lambda _{SR}}}\left[ 1-e^{-\frac{\zeta I_{th}}{ P_{S,max} \lambda _{SP}}} \left( 1-\frac{\zeta I_{th} \lambda _{SR}}{\zeta I_{th} \lambda _{SR} + p\lambda _{SP}}\right) \right] \end{aligned}$$

(35)

$$\begin{aligned} f_P(p)&=\frac{d}{dp}F_P(p) \nonumber \\&=\frac{e^{-\frac{p}{P_{S,max} \lambda _{SR}}}}{P_{S,max} \lambda _{SR}} \left[ 1-e^{-\frac{\zeta I_{th}}{P_{S,max}\lambda _{SP}}}\left[ 1-\frac{\zeta I_{th} \lambda _{SR}}{ \lambda _{SP}} \left( \frac{1}{p+\frac{\zeta I_{th} \lambda _{SR}}{ \lambda _{SP}}} +\frac{P_{S,max} \lambda _{SR}}{(p+\frac{\zeta I_{th} \lambda _{SR}}{ \lambda _{SP}})^2} \right) \right] \right] \end{aligned}$$

(36)

Similarly, the PDF of Q, $f_Q(q)$ can be obtained from (35), by replacing the corresponding distributions as,

$$\begin{aligned}&f_Q(q)=\frac{e^{-\frac{q}{P_{R,max} \lambda _{RR}}}}{P_{R,max} \lambda _{RR}} \Biggl [1-e^{-\frac{(1-\zeta ) I_{th}}{P_{R,max}\lambda _{I_2}}} \bigg [ 1-\frac{(1-\zeta ) I_{th} \lambda _{RR}}{ \lambda _{I_2}} \Bigg (\frac{1}{q+\frac{(1-\zeta ) I_{th} \lambda _{RR}}{ \lambda _{I_2}}} +\frac{P_{R,max} \lambda _{RR}}{(q+\frac{(1-\zeta ) I_{th} \lambda _{RR}}{ \lambda _{I_2}})^2} \Bigg )\bigg ] \Biggr ] \end{aligned}$$

(37)

Now, using the SINRs defined in (6) and (7), the CDF $F_{\varGamma _{R,1}}(\varGamma _{FD,1})$ is derived as follows:

$$\begin{aligned} F_{\varGamma _{R,1}}(\varGamma _{FD,1})&=Pr(\varGamma _{R,1}< \varGamma _{FD,1})\nonumber \\&= Pr \left( \frac{P}{Q+1}<\varGamma _{FD,1} \right) \nonumber \\&=\int _{0}^{\infty } F_P((q+1)\varGamma _{FD,1}) \, f_Q(q) dq \end{aligned}$$

(38)

Making use of the distributions defined earlier in (35) and (37), and [ [40], eqns. (3.352.4) and (3.353.3) ], the integral expression in (38) can be simplified to obtain a closed form expression as shown in (10).

Similarly, let T and U be denoted respectively as,

$T=min \left( P_{R,max},\frac{(1-\zeta ) I_{th}}{\vert h_{RP} \vert ^2} \right) \vert h_{RD} \vert ^2$ and $U=min \left( P_{S,max},\frac{\zeta I _{th}}{ \vert h_{SP} \vert ^2} \right) \vert h_{SD} \vert ^2$.

Now, the CDF $F_{\varGamma _{D,1}}(\varGamma _{FD,1})$ can be evaluated as:

$$\begin{aligned} F_{\varGamma _{D,1}}(\varGamma _{FD,1})&=Pr \,(T+U < \varGamma _{FD,1} ) \nonumber \\&=\int _{0}^{\varGamma _{FD,1}}f_T(t)F_U(\varGamma _{FD,1}-t) dt \end{aligned}$$

(39)

The CDF $F_U(u)$ and the PDF $f_T(t)$ in 39 can be determined from (35), and (36) respectively, by substituting the corresponding distributions, as follows:

$$\begin{aligned} F_U(u)&=1-e^{-\frac{u}{P_{S,max} \lambda _{SD}}}\left[ 1-e^{-\frac{\zeta I_{th}}{ P_{S,max} \lambda _{SP}}} \left( 1-\frac{\zeta I_{th} \lambda _{SD}}{\zeta I_{th} \lambda _{SD} + u\lambda _{SP}}\right) \right] \end{aligned}$$

(40)

$$\begin{aligned} f_T(t)&=\frac{e^{-\frac{t}{P_{R,max} \lambda _{RD}}}}{P_{R,max} \lambda _{RD}} \Biggl [1-e^{-\frac{(1-\zeta ) I_{th}}{P_{R,max}\lambda _{RP}}} \Bigg [ 1-\frac{(1-\zeta ) I_{th} \lambda _{RD}}{ \lambda _{RP}} \Bigg (\frac{1}{t+\frac{(1-\zeta ) I_{th} \lambda _{RD}}{ \lambda _{RP}}} \nonumber \\&\quad +\,\frac{P_{R,max} \lambda _{RD}}{(t+\frac{(1-\zeta ) I_{th} \lambda _{RD}}{ \lambda _{RP}})^2} \Bigg )\Bigg ] \Biggr ] \end{aligned}$$

(41)

Simplifying the integral in (39) using (40), (41) and [40], eqns. (3.352.1) and (3.353.1) ], the closed form solution can be obtained as in (11).

B Derivation of (17) and (18):

The closed form expansion for $F_{\varGamma _{R,2}}(\varGamma _{FD,2})$ is same as that of $F_{\varGamma _{R,1}}(\varGamma _{FD,1})$, which is already proved in “Appendix A”.

The CDF $F_{\varGamma _{D,2}}(\varGamma _{FD,2})$ is defined as :

$$\begin{aligned} F_{\varGamma _{D,2}}(\varGamma _{FD,2})&=Pr(\varGamma _{D,2}< \varGamma _{FD,2})\nonumber \\&= Pr \left( \frac{T}{U+1}<\varGamma _{FD,2} \right) \nonumber \\&=\int _{0}^{\infty } F_T((u+1)\varGamma _{FD,2}) \, f_U(u) du \end{aligned}$$

(42)

Notice that the integral in (42) is identical to that of (38). Therefore, the closed form expression for $F_{\varGamma _{D,2}}(\varGamma _{FD,2})$ given by (18), can be determined from (10) by exchanging $P_{S,max}$ and $P_{R,max}$, and by replacing the mean channel gains of $h_{SR}$, $h_{SP}$, $h_{RP}$ and $h_{RR}$ by that of $h_{RD}$, $h_{RP}$, $h_{SP}$ and $h_{SD}$ respectively.

C Derivation of (23) and (24):

The CDF $F_{\varGamma _{R,3}}(\varGamma _{FD,3})$, given is same as that of $F_{\varGamma _{R,1}}(\varGamma _{FD,1})$. The detailed proof is available in “Appendix A”.

The CDF $F_{\varGamma _{D,3}}(\varGamma _{FD,3})$ is determined as follows:

$$\begin{aligned} F_{\varGamma _{D,3}}(\varGamma _{FD,3})&= Pr(\varGamma _{D,3}< \varGamma _{FD,3}) \nonumber \\&=Pr(\frac{P_R \vert h_{RD} \vert ^2}{N_0}< \varGamma _{FD,3}) \nonumber \\&=Pr(T< \varGamma _{FD,3})= F_T(\varGamma _{FD,3}) \end{aligned}$$

(43)

where T is given by, $T=\frac{P_R }{N_0}\vert h_{RD} \vert ^2$. The derivation for the CDF of T, $F_T(\varGamma _{FD,3})$ is similar to that of $F_P(p)$ derived in (35). Thus, the closed form expression for $F_T(\varGamma _{FD,3})$, can be easily obtained from (35), by substituting $p=\varGamma _{FD,3}$, $P_{S,max}=P_{R,max}$, $\lambda _{SR}=\lambda _{RD}$ and $\lambda _{SP}=\lambda _{RP}$.

D Derivation of (33)

The outage probability of the cognitive HDCRN-MRC scheme is given by,

$$\begin{aligned} P_{out,HD}^{MRC}&=Pr(\varGamma _{DL}+min(\varGamma _{R,4},\varGamma _{D,4}) \le \varGamma _{HD}) \nonumber \\&=Pr(U+V \le \varGamma _{HD}) \nonumber \\&=\int _{0}^{\varGamma _{HD}} f_U(u)F_V(\varGamma _{HD}-u)du \end{aligned}$$

(44)

where $V=min(P,T)$; $P=min \big (P_{S,max},\frac{I_{th}}{ \vert h_{SP} \vert ^2} \big ) \vert h_{SR} \vert ^2$; $T=min \big (P_{R,max},\frac{I_{th}}{\vert h_{RP} \vert ^2} \big ) \vert h_{RD} \vert ^2$. To evaluate the integral in (44), we need to determine the PDF of U and the CDF of V. The PDF $f_U(u)$ is given by,

$$\begin{aligned}&f_U(u)=\frac{e^{-\frac{u}{P_{S,max} \lambda _{SD}}}}{P_{S,max} \lambda _{SD}} \left[ 1-e^{-\frac{I_{th}}{P_{S,max}\lambda _{SP}}}\left[ 1-\frac{I_{th} \lambda _{SD}}{ \lambda _{SP}} \left( \frac{1}{u+\frac{I_{th} \lambda _{SD}}{ \lambda _{SP}}} +\frac{P_{S,max} \lambda _{SD}}{(u+\frac{I_{th} \lambda _{SD}}{ \lambda _{SP}})^2} \right) \right] \right] \end{aligned}$$

(45)

which is obtained from (36), by replacing $\lambda _{SR}$ by $\lambda _{SD}$ and $\zeta =1$.

The CDF $F_V(v)$ is determined as follows:

$$\begin{aligned} F_V(v)&= Pr(V \le v)=Pr(min(P,T) \le v) \nonumber \\&= Pr(P \le v,P \le T) + Pr(T \le v,P \ge T)\nonumber \\&= \underbrace{\int _{0}^{v} [1-F_T(p)]f_P(p)dp}_{K_1(v)} + \underbrace{\int _{0}^{v} [1-F_P(t)]f_T(t) }_{K_2(v)} \end{aligned}$$

(46)

The integral expression for $K_1(v)$ is solved using (35), (36), (36), (41) and [[40] eqns. (3.352.4), (3.353.1) and (3.353.3)] to get,

$$\begin{aligned} K_1(v)&=\frac{1}{\hat{a_0}}\Bigg [ \frac{ (1-\hat{a_1})(1-\hat{b_1})(1-e^{-{\hat{\mu }}}v)}{{\hat{\mu }}}+ \delta _0 e^{\hat{a_0}\hat{a_2}} [Ei(-\hat{a_0} (v+\hat{a_2}))-Ei(-\hat{a_0}\hat{a_2})] \nonumber \\&\quad +\,\delta _1 e^{\hat{a_0}\hat{b_2}} [Ei(-\hat{a_0} (v+\hat{b_2}))-Ei(-\hat{a_0}\hat{b_2})]+\delta _2 \big (1-\frac{e^{-\hat{a_0}v}}{v+\hat{a_2}}-\hat{a_0}e^{\hat{a_2}v Ei(-\hat{a_0}(v+\hat{a_2}))}\big ) \Bigg ] \end{aligned}$$

(47)

where $\hat{a_0}=P_{S,max}\lambda _{SR}$, $\hat{a_1}=e^{-\frac{I_{th}}{P_{S,max}\lambda _{SP}}}$, $\hat{a_2}=\frac{I_{th}\lambda _{SR}}{\lambda _{SP}}$, $\hat{b_0}=P_{R,max}\lambda _{RD}$$\hat{b_1}=e^{-\frac{I_{th}}{P_{R,max}\lambda _{RP}}}$, $\hat{b_2}=\frac{I_{th}\lambda _{RD}}{\lambda _{RP}}$, ${\hat{\mu }}=\frac{1}{P_{R,max}\lambda _{RD}}+\frac{1}{P_{S,max}\lambda _{SR}}$, $\delta _0=\hat{a_1}\hat{a_2}\big [1-\frac{\hat{b_1}\hat{a_2}}{\hat{a_2}-\hat{b_2}}-\frac{\hat{a_0}\hat{b_1}\hat{b_2}}{(\hat{a_2}-\hat{b_2})^2}\big ]$, $\delta _1=\hat{b_1}\hat{b_2}\big [1+ \frac{\hat{a_1}\hat{b_2}}{(\hat{a_2}-\hat{b_2})} +\frac{\hat{a_0}\hat{a_1}\hat{a_2}}{(\hat{a_2}-\hat{b_2})^2}\big ]$ and $\delta _2=\hat{a_0}\hat{a_1}\hat{a_2}(1-\frac{\hat{b_1}\hat{a_2}}{(\hat{a_2}-\hat{b_2})})$. $K_2(v)$ is obtained from $K_1(v)$ by interchanging $\hat{a_i} , i=\{0,1,2\}$ and $\hat{b_i} , i=\{0,1,2\}$ as follows:

$$\begin{aligned} K_2(v)&=\frac{1}{\hat{b_0}}\Bigg [\frac{ (1-\hat{a_1})(1-\hat{b_1})(1-e^{-{\hat{\mu }}}v)}{{\hat{\mu }}} + \delta _0 e^{\hat{b_0}\hat{a_2}} [Ei(-\hat{b_0} (v+\hat{a_2}))-Ei(-\hat{b_0}\hat{a_2})] \nonumber \\&\quad +\,\delta _1 e^{\hat{b_0}\hat{b_2}} [Ei(-\hat{b_0} (v+\hat{b_2}))-Ei(-\hat{b_0}\hat{b_2})] +\delta _3 \big (1-\frac{e^{-\hat{b_0}v}}{v+\hat{b_2}}-\hat{b_0}e^{\hat{b_2}v Ei(-\hat{b_0}(v+\hat{b_2}))}\big )\Bigg ] \end{aligned}$$

(48)

where $\delta _3=\hat{b_0}\hat{b_1}\hat{b_2}(1-\frac{\hat{a_1}\hat{b_2}}{(\hat{a_2}-\hat{b_2})})$. The final expression for $P_{out,HD}^{MRC}$ can be evaluated from (44–47) to get (33). The closed form solution is not obtained, but the integral in (33) can be easily evaluated using numerical integration in Matlab.