Abstract
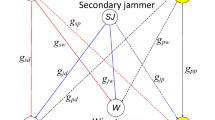
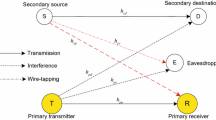
In this paper, we consider the physical-layer security for the primary system in an underlay cognitive radio model which comprises of a primary source–destination pair, a secondary receiver (SR), K secondary transmitters (STi, i = 1,…,K) and an eavesdropper (E). To protecting the transmission confidentiality of the primary transmission system against eavesdropping, we propose secondary transmitter (ST) aided opportunistic jamming transmission protocols. In our protocols, the selection of ST plays a crucial role. To this end, we propose the optimal secondary transmission selection (OSTS) and the Optimal Cooperative Jammer Selection (OCJS), respectively. For the non-security management, OSTS, OCJS schemes, we derive the closed-form expressions of the outage probability and the intercept probability for primary system, respectively. Furthermore, we also derive the closed-form expressions of the outage probability for the secondary user for the selective schemes. Numerical results show that the OCJS scheme has the best security performance and the conventional non-security management scheme has the worst security performance for primary system. In addition, the outage performances of OSTS and OCJS are better than the conventional non-security protocol in high secondary transmitting SNR region.






Similar content being viewed by others
References
Mitola, J., & Maguire, G. Q. (1999). Cognitive radio: Making software radios more personal. IEEE Personal Communications, 6(4), 13–18.
Haykin, S. (2005). Cognitive radio: Brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications, 23(2), 201–220.
Zhang, M., Yang, M., & Wu, Q (2018). Smart perception and autonomic optimization: A novel bio-inspired hybrid routing protocol for MANETs. Future generation computer systems, 81, 505–513.
Rajesh, K. S., & Danda, B. R. (2015). Advances on security threats and countermeasures for cognitive radio networks: A survey. IEEE Communication Surveys and Tutorials, 17(2), 1023–1043.
Li, J., Feng, Z., Feng, Z., & Zhang, P. (2015). A survey of security issues in cognitive radio networks. IEEE Journals and Magazines of China Communication, 12(3), 132–150.
Nguyen, V. D., Hoang, T. M., & Shin, O. S. (2015). Secrecy capacity of the primary system in a cognitive radio network. IEEE Transaction on Vehicular Technology, 64(8), 3834–3843.
Yulong, Z., Xianbin, W., & Weiming, S. (2013). Physical-layer security with multiuser scheduling in cognitive radio networks. IEEE Transactions on Communications, 61(12), 5103–5113.
Zhihui, S., Yi, Q., & Song, C. (2013). On physical layer security for cognitive radio networks. IEEE Network, 27(3), 28–33.
Wyner, A. D. (1975). The wire-tap channel. Bell System Technology Journal, 54(8), 1355–1387.
Leung-Yan-Cheong, S. K., & Hellman, M. E. (1978). The Gaussian wiretap channel. IEEE Transaction Information Theory, 24(4), 451–456.
Goel, S., & Negi, R. (2008). Guaranteeing secrecy using artificial noise. IEEE Transaction Wireless Communication, 7(6), 2180–2189.
Ding, Z., Ma, Z., & Fan, P. (2014). Asymptotic studies for the impact of antenna selection on secure two-way relaying communications with artificial noise. IEEE Transaction Wireless Communication, 13(4), 2189–2203.
Chae, S., Choi, W., Lee, J., & Quek, T. (2014). Enhanced secrecy in stochastic wireless networks: Artificial noise with secrecy protected zone. IEEE Transaction Information Forensics and Security, 9(10), 1617–1628.
Wang, Z., Xiao, M., Skoglund, M., & Poor, H. V. (2015). Secure degrees of freedom of wireless X networks using artificial noise alignment. IEEE Transaction Communication, 63(7), 2632–2646.
Nguyen, V.D., Duong, T.Q., Shin, O.S. (2015). Physical layer security for primary system: A symbiotic approach in cooperative cognitive radio networks. In IEEE Global Communications Conference (pp. 1–6).
Wang, X., Ji, Y., Zhou, H., et al. (2017). Auction based frameworks for secure communications in static and dynamic cognitive radio networks. IEEE Transactions on Vehicular Technology, 66(3), 2658–2673.
Xu, D., & Li, Q. (2016). Resource allocation for cognitive radio with primary user secrecy outage constraint. IEEE System Journal. https://doi.org/10.1109/jsyst.2016.2585654.
Pei, Y., Liang, Y.-C., Teh, K. C., & Li, K. (2011). Secure communication in multiantenna cognitive radio networks with imperfect channel state information. IEEE Transactions Signal Process, 59(4), 1683–1693.
Acknowledgements
This work is partially supported by the National Natural Science Foundation of China (NSFC) under Grants Nos. 61801171, 61701172, 61771185 and 61772175, in part by the Science and Technology Research of Henan Province under Grants Nos. 182102210044 and 182102210285, in part by Key scientific research programs of henan higher education (Nos. 16A510005, 17A520005 and 18A510009), in part by the Science and Technology Development Programs of Henan Province under Grant No. 192102210284.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
Let \(X_{1}\),\(X_{2}\), \(X_{3}\) and \(X_{4}\) be exponentially variables with parameters \({1 \mathord{\left/ {\vphantom {1 {\sigma_{\text{P}}^{2} }}} \right. \kern-0pt} {\sigma_{\text{P}}^{2} }}\), \({1 \mathord{\left/ {\vphantom {1 {\sigma_{{{\text{S}}_{i} {\text{P}}}}^{2} }}} \right. \kern-0pt} {\sigma_{{{\text{S}}_{i} {\text{P}}}}^{2} }}\), \({1 \mathord{\left/ {\vphantom {1 {\sigma_{\text{PE}}^{2} }}} \right. \kern-0pt} {\sigma_{\text{PE}}^{2} }}\) and \({1 \mathord{\left/ {\vphantom {1 {\sigma_{{{\text{S}}_{j} {\text{E}}}}^{2} }}} \right. \kern-0pt} {\sigma_{{{\text{S}}_{j} {\text{E}}}}^{2} }}\), respectively. Moreover, letting \(\tilde{X}_{2} = \beta X_{2} + {{N_{0} } \mathord{\left/ {\vphantom {{N_{0} } {P_{\text{S}} }}} \right. \kern-0pt} {P_{\text{S}} }}\), \(\tilde{X}_{3} = X_{3} + {{N_{0} } \mathord{\left/ {\vphantom {{N_{0} } {P_{\text{S}} }}} \right. \kern-0pt} {P_{\text{S}} }}\), \(Y_{1} = {{X_{1} } \mathord{\left/ {\vphantom {{X_{1} } {\tilde{X}_{2} }}} \right. \kern-0pt} {\tilde{X}_{2} }}\), and \(Y_{2} = {{X_{4} } \mathord{\left/ {\vphantom {{X_{4} } {\tilde{X}_{3} }}} \right. \kern-0pt} {\tilde{X}_{3} }}\). The probability distribution and density of random variables \(\tilde{X}_{2}\) can be derived as (43) and (44), respectively.
By using (44), the probability distribution and density of random variables \(Y_{1}\) can be derived as (45) and (46) respectively.
The probability distribution and density of random variables \(\tilde{X}_{2}\) can be derived as (47) and (48), respectively.
By using (48), the probability distribution and density of random variables \(Y_{2}\) can be derived as (49) and (50) respectively.
Rights and permissions
About this article
Cite this article
Xie, P., Zhu, J., Zhang, M. et al. Aided Opportunistic Jammer Selection for Secrecy Improvement in Underlay Cognitive Radio Networks. Wireless Pers Commun 107, 829–848 (2019). https://doi.org/10.1007/s11277-019-06304-2
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-019-06304-2