A Framework on the Performance Analysis of Cooperative Wireless Body Area Networks

Abstract

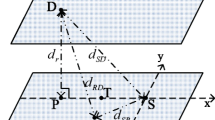
Wireless body area networks (WBANs) are deal with wireless networks in the human body. We describe the performance analysis of dual-hop cooperative relaying systems employing amplify-and-forward (AF) technique in WBANs over independent and nonnecessary identically distributed Gamma fading channels. More specifically, we present closed-form derivations of the outage probabilities (OP), symbol error probabilities (SEP) and ergodic capacity (EC) for fixed gain and channel state information (CSI)-assisted relaying techniques at arbitrary signal-to-noise-ratios (SNRs). We also deduce novel expressions in the high SNR region. By doing so, we can quantify the performance of system by the diversity and coding gains. Using the derived expressions as a starting point and for the case of Exponential fading, we consider three practical optimization scenarios. They are optimal relay position with fixed power allocation, power allocation under the fixed location of the relay and joint optimization of power allocation and relay position under a transmit power constraint. The Monte Carlo simulations are used to validate the accuracy of our derivations, where it is demonstrated that the proposed adaptive allocation method significantly outperforms the fixed allocation method.

Appendix

1.1 Proof of Proposition 1

By employing (7), the OP of dual-hop relaying assuming the fixed gain relaying technique can be expressed as

$$\begin{aligned} {{P}_{\mathrm{out}}^F}({{\gamma }_{\mathrm{th}}})=\Pr [\gamma _{\mathrm{e2e}}^{{F}}<{{\gamma }_{\mathrm{th}}}]=\Pr \left[ \frac{{{\gamma }_{1}}{{\gamma }_{2}}}{C+{{\gamma }_{2}}}<{{\gamma }_{\mathrm{th}}} \right] \end{aligned}$$

(63)

Using the probability conditioning technique on $\gamma _{2}$ RV, we can rewrite (63) as bellows

$$\begin{aligned} {{P}_{\mathrm{out}}^F}({{\gamma }_{\mathrm{th}}})=\int \limits _{0}^{\infty }{{\mathrm{Pr}} \left[ \frac{{{\gamma }_{1}}{{\gamma }_{2}}}{C+{{\gamma }_{2}}} < {{\gamma }_{\mathrm{th}}}\left| {{\gamma }_{2}} \right. \right] }{{f}_{{{\gamma }_{2}}}}({{\gamma }_{2}})d{{\gamma }_{2}} \end{aligned}$$

(64)

Putting (4) and (5) in (64), and by separating (64) into two cases for odd and even values of i, we get

$$\begin{aligned} {{P}_{\mathrm{out}}^F}({{\gamma }_{\mathrm{th}}}) = 1-{P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})-{P_{out}^{F,\mathrm{odd}}}({\gamma _{\mathrm{th}}}) \end{aligned}$$

(65)

The OP in (64) for the even values of i can be obtained as

$$\begin{aligned} {P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})=&\sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}}}{{i!}}}\left( {\gamma _{\mathrm{th}}}\right) ^{\frac{i}{2}}\frac{{{b^n}}}{{\varGamma (n)}} \sum \limits _{k = 0}^j {\frac{{j!{C^k}}}{{k!\left( {j - k} \right) !}}} \int \limits _0^\infty { {u^{n - 2k - 1}}} {e^{ - bu - a\sqrt{{\gamma _{\mathrm{th}}}(1 + \frac{C}{{{u^{2}}}})}}}du \end{aligned}$$

(66)

where we set $j = \frac{i}{2}$. Employing [35, Eqs. (1.39)], we can solve the integral in (66) in terms of Meijer’s-G function, defined in [32, Eq. (9.301)], as follows

$$\begin{aligned} {P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})&= \frac{{{b^n}}}{{\varGamma (n)}}\sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}\left( {\gamma _{\mathrm{th}}}\right) ^{\frac{i}{2}}}}{{i!}}} \sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) \int \limits _0^\infty {{u^{n - 2k - 1}}} G_{0,1}^{1,0}\nonumber \\&\left[ {{{\left( {{a^{2}}{\gamma _{\mathrm{th}}}\left( 1 + \frac{C}{{{u^{2}}}}\right) } \right) }^{\frac{1}{2}}}\left| {_0^ - } \right. } \right] G_{0,1}^{1,0}\left[ {bu\left| {_0^ - } \right. } \right] du \end{aligned}$$

(67)

The integral variable u can be substituted by $\tau$ parameter with ${a^{2}}{\gamma _{\mathrm{th}}}\frac{C}{{{u^{2}}}} = \tau$. Then, we get

$$\begin{aligned} {P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})&= \frac{{{b^n}}}{{\varGamma (n)}}\sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}{\gamma _{\mathrm{th}}}^{\frac{i}{2}}}}{{i!}}{{({a^{2}}{\gamma _{\mathrm{th}}})}^{\frac{{n - 2k}}{2}}}} \sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) {C^k} \int \limits _0^\infty {{\tau ^{k - 1 - \frac{n}{2}}}} G_{0,1}^{1,0}\nonumber \\&\left[ {{{\left( {\sigma + \tau } \right) }^{\frac{1}{2}}}\left| {_0^ - } \right. } \right] G_{0,1}^{1,0}\left[ {\omega {\tau ^{ - \frac{1}{2}}}\left| {_0^ - } \right. } \right] d\tau \end{aligned}$$

(68)

By applying [39, Eq. (07.34.02.0001.01)] and [32, Eqs. (3.194.3, 8.384.1)] to (68) , we end up with

$$\begin{aligned} {P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})&= \frac{{{b^n}}}{{\varGamma (n)}}\sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}{\gamma _{\mathrm{th}}}^{\frac{i}{2}}}}{{i!}}{{({a^{2}}{\gamma _{\mathrm{th}}})}^{\frac{{n - 2k}}{2}}}} \sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) \frac{{{C^{\frac{n}{2}}}}}{{4{\pi ^{2}}}} \sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) \nonumber \\&\quad\times \int \limits _{{C_{1}}}\int \limits _{{C_{2}}}\varGamma \left( \frac{s}{2} - \frac{t}{2} - \alpha \right) \frac{{\varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) }}\varGamma (t)\varGamma (\alpha + \frac{t}{2}) \nonumber \\&\quad\times {{\left( \frac{{{\sigma ^{\frac{1}{2}}}}}{\omega }\right) }^t}{{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s}dsdt \end{aligned}$$

(69)

while the integral counters in s and t domains are denoted by $C_{1}$ and $C_{2}$, respectively. The integral form of bivariate Fox-H function in [33, Eq. (1.1)] can be applied to (69) to get

$$\begin{aligned} {P_{out}^{F,\mathrm{even}}}({\gamma _{\mathrm{th}}})&= \frac{{{b^n}}}{{\varGamma (n)}}\sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}{\gamma _{\mathrm{th}}}^{\frac{i}{2}}}}{{i!}}{{({a^{2}}{\gamma _{\mathrm{th}}})}^{\frac{{n - 2k}}{2}}}} \sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) {C^{\frac{n}{2}}}\sum \limits _{k = 0}^j \left( \begin{array}{l} j\\ k \end{array} \right) H_{1,0;0,2;1,2}^{0,1;1,0;1,1}\nonumber \\&\left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{1}{{\sqrt{\sigma }}}}\left| {_{( - ;0.5)}^{(1 + \alpha ;0.5, - 0.5),(1;1),(1;1)}} \right. } \right] \end{aligned}$$

(70)

If we set $i = 2j + 1$ which corresponds to odd values of i, we obtain

$$\begin{aligned} {P_{out}^{F,\mathrm{odd}}}({\gamma _{\mathrm{th}}}) = \sum \limits _{i = 0}^{m - 1} {\frac{{{a^i}}}{{i!}}} \left( {\gamma _{\mathrm{th}}}\right) ^{\frac{i}{2}}\frac{{{b^n}}}{{\varGamma (n)}} \int \limits _0^\infty {{\gamma _{2}}^{\frac{n}{2} - 1}{{\left( 1 + \frac{C}{{{\gamma _{2}}}}\right) }^{\frac{{2j + 1}}{2}}}} {e^{ - b\sqrt{{\gamma _{2}}} - a\sqrt{\frac{{{\gamma _{\mathrm{th}}}({\gamma _{2}} + C)}}{{{\gamma _{2}}}}}}}d{\gamma _{2}} \end{aligned}$$

(71)

Applying the binomial expansion [39, Eq. (1.111)] and employing integration by part, the outage probability in (64) assuming odd values for i can be written as

$$\begin{aligned} {P_{out}^{F,\mathrm{odd}}}({\gamma _{th}})&= \sum \limits _{\underbrace{i = 1}_{i ~\mathrm {is ~ odd}}}^{m - 1} \sum \limits _{k = 0}^{j=\frac{i-1}{2}} {\frac{{{a^i}}}{{i!}}} \left( {\gamma _{th}}\right) ^{\frac{i}{2}}\frac{{{b^n}}}{{2\varGamma (n)}} {\frac{{j!{C^k}}}{{k!\left( {j - k} \right) !}}}\nonumber \\&\Bigg \{ - \frac{{2\left( \frac{n}{2} + 1 - k\right) }}{{aC\sqrt{{\gamma _{th}}} }}\int \limits _0^\infty {{\gamma _{2}}^{\frac{n}{2} - k}{e^{ - b\sqrt{{\gamma _{2}}} - a\sqrt{{\gamma _{th}}\left( 1 + \frac{C}{{{\gamma _{2}}}}\right) } }}} d{\gamma _{2}}\nonumber \\&\quad+\, \frac{b}{{aC\sqrt{{\gamma _{th}}}}}\int \limits _0^\infty {{\gamma _{2}}^{\frac{n}{2} + \frac{1}{2} - k}} {e^{ - b\sqrt{{\gamma _{2}}} - a\sqrt{{\gamma _{th}}\left( 1 + \frac{C}{{{\gamma _{2}}}}\right) }}}d{\gamma _{2}}\nonumber \\&\quad-\, \frac{{2\left( \frac{n}{2} - k\right) }}{{a\sqrt{{\gamma _{th}}}}}\int \limits _0^\infty {{\gamma _{2}}^{\frac{n}{2} - k - 1}} {e^{ - b\sqrt{{\gamma _{2}}} - a\sqrt{{\gamma _{th}}\left( 1 + \frac{C}{{{\gamma _{2}}}}\right) }}}d{\gamma _{2}}\nonumber \\&\quad+\, \frac{b}{{a\sqrt{{\gamma _{th}}}}}\int \limits _0^\infty {{\gamma _{2}}^{\frac{n}{2} - \frac{1}{2} - k}} {e^{ - b\sqrt{{\gamma _{2}}} - a\sqrt{{\gamma _{th}}\left( 1 + \frac{C}{{{\gamma _{2}}}}\right) }}}d{\gamma _{2}}\Bigg \} \end{aligned}$$

(72)

The same procedure that used in (67), (68) and (69) can be used in order to obtain the OP of fixed gain AF relaying for odd values of i. Finally, by substituting into (65) we get (8).

1.2 Proof of Proposition 2

By putting (4) and (5) in (64) and employing [39, Eq. (06.06.06.0001.02)], we get

$$\begin{aligned} {{P}_{out}^F}({{\gamma }_{\mathrm{th}}})&\approx \int \limits _{0}^{\infty }{\frac{{{\left( a\sqrt{\frac{{{\gamma }_{\mathrm{th}}}(C+{{\gamma }_{2}})}{{{\gamma }_{2}}}} \right) }^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}}{{({{\gamma }_{2}})}^{\frac{n}{2}-1}}{{e}^{-b\sqrt{{{\gamma }_{2}}}}}d{{\gamma }_{2}} \nonumber \\&\approx \frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}\int \limits _{0}^{\infty }{{{({{\gamma }_{2}}+C)}^{\frac{m}{2}}}{{\gamma }_{2}}^{\frac{n-m}{2}-1}}{{e}^{-b\sqrt{{{\gamma }_{2}}}}}d{{\gamma }_{2}} \end{aligned}$$

(73)

Using [35, Eq. (1.39)], the integral in (73) can be rewritten as follow

$$\begin{aligned} {P_{out}^F}({\gamma _{th}}) \approx \frac{{{{\left( {a\sqrt{{\gamma _{th}}} } \right) }^m}}}{{\varGamma (m + 1)}}\frac{{{b^n}}}{{2\varGamma (n)}}\int \limits _0^\infty {\frac{{{\gamma ^{\frac{{n - m}}{2} - 1}}}}{{{{\left( {\gamma + C} \right) }^{ - \frac{m}{2}}}}}} G_{0,1}^{1,0}\left[ {b\sqrt{\gamma } \left| {_0^ - } \right. } \right] d\gamma \end{aligned}$$

(74)

By applying [39, Eq. (07.34.21.0086.01)] to (74), we arrive to (9).

1.3 Proof of Proposition 3

This proposition can be proved by assuming even integer values of the fading severity parameter of the first link. Applying the binomial expansion [39, Eq. (1.111)], we end up with

$$\begin{aligned} {{P}_{out}^F}({{\gamma }_{\mathrm{th}}})&\approx \frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}\int \limits _{0}^{\infty }{{{({{x}^{2}}+C)}^{\frac{m}{2}}}{{x}^{n-m-1}}}{{e}^{-bx}}dx\nonumber \\&= \frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{\varGamma (n)}\int \limits _{0}^{\infty }{\sum \limits _{k=0}^{\frac{m}{2}}{\frac{\left( \frac{m}{2} \right) !}{k!\left( \frac{m}{2}-k \right) !}}{{x}^{2(\frac{m}{2}-k)}}{{C}^{k}}{{x}^{n-m-1}}}{{e}^{-bx}}dx \end{aligned}$$

(75)

Using the variable change method $\sqrt{\gamma }=x$, we have

$$\begin{aligned} {{P}_{out}^F}({{\gamma }_{\mathrm{th}}})\approx \frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{\varGamma (n)}\sum \limits _{k=0}^{\frac{m}{2}}{\frac{\left( \frac{m}{2} \right) !{{C}^{k}}}{k!\left( \frac{m}{2}-k \right) !}}\int \limits _{0}^{\infty }{{{x}^{n-2k-1}}}{{e}^{-bx}}dx \end{aligned}$$

(76)

Applying [39, Eq. (3.351.3)] to (76), we arrive in (10).

1.4 Proof of Proposition 4

If we put (69) and (72) in (11), we can write

$$\begin{aligned} \overline{{{P}_{e}}}^F&= \frac{1}{2} + \frac{1}{2}\sqrt{\frac{d}{\pi }} \sum \limits _{\underbrace{i = 0}_{i ~\mathrm {is ~ even}}}^{m - 1} {\sum \limits _{k = 0}^{j=\frac{i}{2}} \left( \begin{array}{l} j\\ k \end{array} \right) \frac{{{a^i}}}{{i!}}} \frac{{{b^n}}}{{2\varGamma (n)}}\int \limits _0^\infty {\frac{{{e^{ - d\gamma }}{\gamma ^{\frac{i}{2}}}}}{{\sqrt{\gamma }}}} H_{1,0;0,2;1,2}^{0,1;1,0;1,1}\nonumber \\&\quad\times\left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{{\sqrt{d}}}{{\sqrt{\sigma }}}}\left| {_{( - ;0.5)}^{(1 + k - \frac{n}{2};0.5, - 0.5),(1;1),(1;1)}} \right. } \right] \nonumber \\&\quad +\,\frac{1}{2}\sqrt{\frac{d}{\pi }} \sum \limits _{\underbrace{i = 1}_{i ~\mathrm {is ~ odd}}}^{m - 1} {\sum \limits _{k = 0}^{j=\frac{i-1}{2}} \left( \begin{array}{l} j\\ k \end{array} \right) \frac{{{a^i}}}{{i!}}} \frac{{{b^n}}}{{2\varGamma (n)}}\int \limits _0^\infty {\frac{{{e^{ - d\gamma }}{\gamma ^{\frac{i}{2}}}}}{{\sqrt{\gamma }}}} \nonumber \\&\quad\times\Bigg \{ \frac{{2\left( \frac{n}{2} + 1 - k\right) }}{{a\sqrt{{\gamma }}}}H_{1,0;0,2;1,2}^{0,1;1,0;1,1} \left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{{\sqrt{d}}}{{\sqrt{\sigma }}}} \left| {_{( - ;0.5)}^{\left( k - \frac{n}{2};0.5, - 0.5\right) ,(1;1),(1;1)}} \right. } \right] \nonumber \\&\quad-\, \frac{{b{\sqrt{C}}}}{{a\sqrt{{\gamma }}}}H_{1,0;0,2;1,2}^{0,1;1,0;1,1} \left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{{\sqrt{d}}}{{\sqrt{\sigma }}}} \left| {_{( - ;0.5),}^{\left( k - \frac{{n + 1}}{2};0.5, - 0.5\right) ,(1;1),(1;1)}} \right. } \right] \nonumber \\ &\quad+\, \frac{{2\left( \frac{n}{2} - k\right) }}{{a\sqrt{{\gamma }}}}H_{1,0;0,2;1,2}^{0,1;1,0;1,1}\left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{{\sqrt{d}}}{{\sqrt{\sigma }}}}\left| {_{( - ;0.5)}^{(1 + k - \frac{n}{2};0.5, - 0.5),(1;1),(1;1)}} \right. } \right] \nonumber \\&-\, \frac{{b{\sqrt{C}}}}{{a\sqrt{{\gamma }}}}H_{1,0;0,2;1,2}^{0,1;1,0;1,1}\left[ {_{\frac{{\sqrt{\sigma }}}{\omega }}^{\frac{{\sqrt{d}}}{{\sqrt{\sigma }}}}\left| {_{( - ;0.5)}^{\left( k - \frac{{n - 1}}{2};0.5, - 0.5\right) ,(1;1),(1;1)}} \right. } \right] \Bigg \}d\gamma \end{aligned}$$

(77)

The integrals in (77) can be solved by applying [32, Eq. (3.351.3)]. Finally, utilizing [35, Eq. (2.56)], we get (12).

1.5 Proof of Proposition 5

By putting (9) in (11), we have

$$\begin{aligned} \overline{P_e}^F \approx \frac{1}{2}\sqrt{\frac{d}{\pi }} \int \limits _0^\infty {\frac{{{e^{ - d\gamma }}}}{{\sqrt{\gamma }}}} \frac{{{{(a\sqrt{{\gamma _{th}}} )}^m}}}{{\varGamma (m + 1)}}\frac{{{b^n}}}{{2\varGamma (n)}}\frac{{{C^{\frac{n}{2}}}}}{{\sqrt{\pi } \varGamma \left( - \frac{m}{2}\right) }}G_{1,3}^{3,1}\left[ {\frac{{{b^{2}}C}}{4}\left| {_{ - \frac{n}{2},0,\frac{1}{2}}^{1 - \left( \frac{{n - m}}{2}\right) }} \right. } \right] d\gamma \end{aligned}$$

(78)

The integral in [32, Eq. (3.381.4)] can be used to arrive us to (13).

1.6 Proof of Proposition 6

Putting (10) in (11), we obtain

$$\begin{aligned} \overline{{{P}_{e}}}^F&\approx \frac{1}{2}-\frac{1}{2}\sqrt{\frac{d}{\pi }}\frac{{{a}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{\varGamma (n)}\sum \limits _{k=0}^{\frac{m}{2}}{\frac{\left( \frac{m}{2} \right) !}{k!\left( \frac{m}{2}-k \right) !}} \frac{{{C}^{k}}\varGamma (n-2k)}{{{b}^{n-2k}}}\int \limits _{0}^{\infty }{{{\gamma }^{\frac{m-1}{2}}}{{e}^{-d\gamma }}d\gamma } \end{aligned}$$

(79)

Utilizing [32, Eq. (3.351.3)], we derive (79).

1.7 Proof of Proposition 7

By putting (69) and (72) in (16), we can obtain

$$\begin{aligned} \overline{C}^F&= \frac{{{b^n}{C^{\frac{n}{2}}}}}{{16{\pi ^{2}}\ln 2\varGamma (n)}} \sum \limits _{\underbrace{i = 0}_{i ~\mathrm {is ~ even}}}^{m - 1} {\sum \limits _{k = 0}^{j=\frac{i}{2}} \left( {\begin{array}{c}j\\ k\end{array}}\right) \frac{{{a^i}}}{{i!}}} \int \limits _{{C_{1}}} \int \limits _{{C_{2}}} \frac{{\varGamma \left( \frac{s}{2} - \frac{t}{2} - \alpha \right) \varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) \varGamma (1 - s)}}\nonumber \\&\frac{{\varGamma (t)\varGamma \left( \alpha + \frac{t}{2}\right) }}{{\varGamma (1 - t)}}{{\left( \frac{{{\sigma ^{\frac{1}{2}}}}}{\omega }\right) }^t} {{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s} \times {{\varGamma \left( \frac{{i - s}}{2} + 1\right) \varGamma \left( - \frac{{i - s}}{2}\right) }}dsdt\nonumber \\&+ \frac{{{b^n}{C^{\frac{n}{2}}}}}{{16{\pi ^{2}}\ln 2\varGamma (n)}}\sum \limits _{\underbrace{i = 1}_{i ~\mathrm {is ~ odd}}}^{m - 1} {\sum \limits _{k = 0}^{j=\frac{i-1}{2}} \left( {\begin{array}{c}j\\ k\end{array}}\right) \frac{{{a^i}}}{{i!}}}\nonumber \\&\times \Bigg [\frac{{\left( \frac{n}{2} + 1 - k\right) }}{{ - 2a{\pi ^{2}}}} \int \limits _{{C_{1}}} \int \limits _{{C_{2}}} \frac{{\varGamma \left( \frac{s}{2} - \frac{t}{2} + 1 - \alpha \right) \varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) \varGamma (1 - s)}}\frac{{\varGamma (t)\varGamma \left( \alpha - 1 + \frac{t}{2}\right) }}{{\varGamma (1 - t)}}\nonumber \\&{{\left( \frac{{{\sigma ^{\frac{1}{2}}}}}{\omega }\right) }^t}{{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s} \frac{{\varGamma \left( \frac{{i - s + 1}}{2}\right) \varGamma \left( 1 - \frac{{i - s + 1}}{2}\right) }}{{\varGamma (1)}}dsdt\nonumber \\&+\frac{{b{\sqrt{C}}}}{{4a{\pi ^{2}}}}\int \limits _{{C_{1}}} \int \limits _{{C_{2}}} \frac{{\varGamma \left( \frac{s}{2} - \frac{t}{2} + \frac{3}{2} - \alpha \right) \varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) \varGamma (1 - s)}}\frac{{\varGamma (t)\varGamma \left( \alpha - \frac{3}{2} + \frac{t}{2}\right) }}{{\varGamma (1 - t)}}\nonumber \\&{{\left( \frac{{{\sigma ^{\frac{1}{2}}}}}{\omega }\right) }^t}{{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s}\frac{{\varGamma \left( \frac{{i - s + 1}}{2}\right) \varGamma \left( 1 - \frac{{i - s + 1}}{2}\right) }}{{\varGamma (1)}} dsdt\nonumber \\&+\,\frac{{\left( \frac{n}{2} - k\right) }}{{ - 2a{\pi ^{2}}}}\int \limits _{{C_{1}}} \int \limits _{{C_{2}}} \frac{{\varGamma \left( \frac{s}{2} - \frac{t}{2} - \alpha \right) \varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) \varGamma (1 - s)}} \frac{{\varGamma (t)\varGamma \left( \alpha + \frac{t}{2}\right) }}{{\varGamma (1 - t)}} {{(\frac{{{\sigma ^{\frac{1}{2}}}}}{\omega })}^t}{{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s} \nonumber \\&\frac{{\varGamma \left( \frac{{i - s + 1}}{2}\right) \varGamma \left( 1 - \frac{{i - s + 1}}{2}\right) }}{{\varGamma (1)}}dsdt\nonumber \\&+\,\frac{{b{\sqrt{C}}}}{{4a{\pi ^{2}}}} \int \limits _{{C_{1}}} \int \limits _{{C_{2}}} \frac{{\varGamma \left( \frac{s}{2} - \frac{t}{2} + \frac{1}{2} - \alpha \right) \varGamma (s)}}{{\varGamma \left( \frac{s}{2}\right) \varGamma (1 - s)}}\frac{{\varGamma (t)\varGamma (\alpha - \frac{1}{2} + \frac{t}{2})}}{{\varGamma (1 - t)}}{{\left( \frac{{{\sigma ^{\frac{1}{2}}}}}{\omega }\right) }^t}\nonumber \\&{{\left( \frac{1}{{{\sigma ^{\frac{1}{2}}}}}\right) }^s}\frac{{\varGamma \left( \frac{{i - s + 1}}{2}\right) \varGamma \left( 1 - \frac{{i - s + 1}}{2}\right) }}{{\varGamma (1)}} dsdt\Bigg ] \end{aligned}$$

(80)

The integrals in (80) are solved by using [32, Eqs. (3.241.2, 8.384.1)]. Utilizing [35, Eq. (2.56)], we get (19).

1.8 Proof of Proposition 8

By employing (20), the outage probability of CSI-assisted relaying SNR is obtained as follows

$$\begin{aligned} {{F}_{\gamma _{e2e}^{V}}}({{\gamma }_{\mathrm{th}}})=\Pr [\gamma _{e2e}^{V}<{{\gamma }_{\mathrm{th}}}]=\Pr [{{\gamma }_{1}}({{\gamma }_{2}}-{{\gamma }_{\mathrm{th}}})<{{\gamma }_{2}}{{\gamma }_{\mathrm{th}}}] \end{aligned}$$

(81)

Therefore, we end up with

$$\begin{aligned} {{F}_{\gamma _{e2e}^{V}}}({{\gamma }_{\mathrm{th}}})&= {{\mathbb E}_{{{\gamma }_{2}}}}\left[ \Pr ({{\gamma }_{1}}({{\gamma }_{2}}-{{\gamma }_{\mathrm{th}}})<{{\gamma }_{2}}{{\gamma }_{\mathrm{th}}})\left| {{\gamma }_{2}} \right. \right] \nonumber \\&= \underbrace{{{\mathbb E}_{{{\gamma }_{2}}}}\left[ \Pr \left( {{\gamma }_{1}}<\frac{{{\gamma }_{2}}{{\gamma }_{\mathrm{th}}}}{{{\gamma }_{2}}-{{\gamma }_{\mathrm{th}}}}\left| {{\gamma }_{2}}>{{\gamma }_{\mathrm{th}}} \right. \right) \right] }_I+{{F}_{{{\gamma }_{2}}}}\left( {{\gamma }_{\mathrm{th}}} \right) \end{aligned}$$

(82)

Substituting (4) and (5) into I and using [39, Eq. (06.06.06.0001.02)], we have (83) in our hands

$$\begin{aligned} I&= \int \limits _{{{\gamma }_{\mathrm{th}}}}^{\infty }{\frac{{{(a\sqrt{\frac{{{\gamma }_{2}}{{\gamma }_{\mathrm{th}}}}{{{\gamma }_{2}}-{{\gamma }_{\mathrm{th}}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}}{{({{\gamma }_{2}})}^{\frac{n}{2}-1}}{{e}^{-b\sqrt{{{\gamma }_{2}}}}}d{{\gamma }_{2}}\nonumber \\&= \frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}\int \limits _{{{\gamma }_{\mathrm{th}}}}^{\infty }{{{({{\gamma }_{2}}-{{\gamma }_{\mathrm{th}}})}^{-\frac{m}{2}}}{{\gamma }_{2}}^{\frac{n+m}{2}-1}}{{e}^{-b\sqrt{{{\gamma }_{2}}}}}d{{\gamma }_{2}} \end{aligned}$$

(83)

Utilizing [39, Eq. (07.34.02.0001.01)], (83) may be rewritten in terms of Meijer’s-G function as

$$\begin{aligned} I=\frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}\int \limits _{{{\gamma }_{\mathrm{th}}}}^{\infty }{{{\gamma }^{\frac{n+m}{2}-1}}{{(\gamma -{{\gamma }_{\mathrm{th}}})}^{-\frac{m}{2}}}}G_{0,1}^{1,0}\left[ b\sqrt{\gamma }\left| _{0}^{-} \right. \right] d\gamma \end{aligned}$$

(84)

By employing the integral in [39, Eq. (07.34.21.0085.01)], we obtain the first OP expression as in (21). The second expression of (82) can be expressed as

$$\begin{aligned} {{F}_{{{\gamma }_{2}}}}\left( {{\gamma }_{\mathrm{th}}} \right) =\frac{{{(a\sqrt{{{\gamma }_{\mathrm{th}}}})}^{m}}}{\varGamma (m+1)}\frac{{{b}^{n}}}{2\varGamma (n)}\int \limits _{0}^{\infty }{{{({{\gamma }_{2}})}^{\frac{n}{2}-1}}{{e}^{-b\sqrt{{{\gamma }_{2}}}}}d{{\gamma }_{2}}} \end{aligned}$$

(85)

By utilizing the variable change method $\sqrt{\gamma }=x$ and applying [32, Eqs. (3.462.1, 9.240)], (85) can be simplified. Then by putting (85) and (84) in (82), we arrive in (21).

1.9 Proof of Proposition 9

Using (22), the outage probability of dual-hop AF relaying assuming CSI-assisted relaying technique is obtained as

$$\begin{aligned} {{P}_{out}^V}({{\gamma }_{\mathrm{th}}})={{F}_{{{\gamma }_{1}}}}({{\gamma }_{\mathrm{th}}})+{{F}_{{{\gamma }_{2}}}}({{\gamma }_{\mathrm{th}}})-{{F}_{{{\gamma }_{1}}}}({{\gamma }_{\mathrm{th}}}){{F}_{{{\gamma }_{2}}}}({{\gamma }_{\mathrm{th}}}) \end{aligned}$$

(86)

By employing (5), we can write

$$\begin{aligned} {{F}_{{{\gamma }_{1}}}}\left( \gamma \right) =1-{{e}^{-a\sqrt{\gamma }}}\sum \limits _{i=0}^{m-1}{\frac{{{a}^{i}}{\left( {\sqrt{\gamma }}\right) ^{i}}}{i!}} \end{aligned}$$

(87)

$$\begin{aligned} {{F}_{{{\gamma }_{2}}}}\left( \gamma \right) =1-{{e}^{-b\sqrt{\gamma }}}\sum \limits _{j=0}^{n-1}{\frac{{{b}^{j}}{\left( {\sqrt{\gamma }}\right) ^{j}}}{j!}} \end{aligned}$$

(88)

Substituting (87) and (88) into (86) results in (23).

1.10 Proof of Proposition 10

By putting (21) in (11), the symbol error probability of dual-hop CSI-assisted relaying can be expressed as

$$\begin{aligned} \overline{ P_e}^V&= \frac{1}{2}\sqrt{\frac{d}{\pi }} \int \limits _0^\infty {\frac{{{e^{ - d\gamma }}}}{{\sqrt{\gamma }}}} \left( \frac{{{{(a\sqrt{\gamma } )}^m}}}{{\varGamma (m + 1)}}\frac{{{b^n}}}{{2\varGamma (n)}}\frac{{\varGamma \left( - \frac{m}{2} + 1\right) }}{{\sqrt{\pi } {\gamma ^{ - \frac{n}{2}}}}}G_{1,3}^{3,0}\left[ {\frac{{{b^{2}}\gamma }}{4}\left| {_{\left( - \frac{n}{2},0,\frac{1}{2}\right) }^{\left( 1 - \frac{{m + n}}{2}\right) }} \right. } \right] \right. \nonumber \\&\left. + 1 - \frac{{\varGamma (n,b\sqrt{\gamma } )}}{{\varGamma (n)}} \right) d\gamma \end{aligned}$$

(89)

Applying [35, Eq. (1.39)] and [39, Eq. (07.34.21.0088.01)], we get (24).

1.11 Proof of Proposition 11

By putting (23) in (11), the symbol error probability of dual-hop CSI-assisted relaying is obtained as

$$\begin{aligned} \overline{{{P}_{e}}}^V=\frac{1}{2}-\frac{1}{2}\sqrt{\frac{d}{\pi }}\sum \limits _{i=0}^{m-1}{\sum \limits _{j=0}^{n-1}{\frac{{{a}^{i}}{{b}^{j}}}{i!j!}}}\int \limits _{0}^{\infty }{\frac{{{e}^{-d\gamma }}}{\sqrt{\gamma }}}{{e}^{-(a+b)\sqrt{\gamma }}}{{\left( \gamma \right) }^{\frac{i+j}{2}}}d\gamma \end{aligned}$$

(90)

By utilizing the variable change method $x=\sqrt{\gamma },$ and applying [32, Eq. (8.310.1)] and following some mathematical manipulations, we get (25).

1.12 Proof of Proposition 12

Substituting (21) into (16), the average channel capacity of dual-hop CSI-assisted AF relaying is derived by

$$\begin{aligned} \overline{C}^V = \frac{1}{{2\ln 2}}\int \limits _0^\infty {\frac{{\left[ { - \frac{{{{(a\sqrt{\gamma } )}^m}}}{{\varGamma (m + 1)}}\frac{{{b^n}}}{{2\varGamma (n)}}\frac{{\varGamma ( - \frac{m}{2} + 1)}}{{\sqrt{\pi } {\gamma ^{ - \frac{n}{2}}}}}G_{1,3}^{3,0}\left[ {\frac{{{b^{2}}{\gamma _{\mathrm{th}}}}}{4}\left| {_{ - \frac{n}{2},0,\frac{1}{2}}^{1 - \frac{{m + n}}{2}}} \right. } \right] + \frac{{\varGamma (n,b\sqrt{\gamma } )}}{{\varGamma (n)}}} \right] }}{{1 + \gamma }}} d\gamma \end{aligned}$$

(91)

By applying [35, Eq. (07.34.21.0011.01)] and [32, Eq. (3.389.6)], (26) is derived.

1.13 Proof of Proposition 13

By putting (23) in (16), the average channel capacity of dual-hop CSI-assisted relaying can be expressed as

$$\begin{aligned} {\bar{C}^V} = \frac{1}{{2\ln 2}}\sum \limits _{k = 0}^{m - 1} {\sum \limits _{j = 0}^{n - 1} {\frac{{{a^k}{b^j}}}{{k!j!}}} } \int \limits _0^\infty {\frac{{{e^{ - (a + b)\sqrt{\gamma }}}{{\left( \gamma \right) }^{\frac{{k + j}}{2}}}}}{{1 + \gamma }}} \end{aligned}$$

(92)

Utilizing the variable change method $x=\sqrt{\gamma }$ and applying [32, Eq. (3.389.2.7)], we end up with (27).