Distributed Adaptive Cooperative Bandwidth Spectrum Sensing for Cognitive MIMO Radios

Abstract

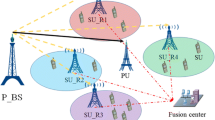
To allow secondary and primary concurrent transmissions achieving optimal spectrum utilization in cognitive radio networks (CRNs), this paper proposes an innovative distributed cooperative spectrum sensing methodology using adaptive sensing bandwidth entitled distributed adaptive cooperative bandwidth spectrum sensing (DACB-SS) scheme when multiple secondary users (SUs) use part of the bandwidth to collaboratively perform spectrum sensing throughout the whole frame to detect the primary user (PU)'s reappearance in time. The SU’s spectrum efficiency is maximized by jointly optimizing the sensing bandwidth proportion, the number of cooperative SUs, and the detection probability, subject to the constraints on the SUs’ interference and the false alarm probability. A gripping slant of DACB-SS regime is provided to maintain overall maximum spectral efficiency. Another contribution of DACB-SS algorithm is the benefit to make great improvement on the sum capacity to obtain better performance of spectrum coexistence. Simulation results illustrate that the proposed analytical model investigates characteristic changes of the spectrum usage affected by the outage probability of PR and the coexisting secondary transmission bandwidth in terms of overall spectral efficiency as well as the outage capacity which can be characterized by the outage probability of SR and the interference from ST to PR in multiuser multiple-input multiple-output broadcast channel (MU-MIMO-BC). Besides, the sum capacity is impacted by channel gains, primary transmit power and secondary transmit power in Gaussian cognitive inference channel (G-CIFC).

Appendix 1

Proof of Theorem 3.2.

The first-order and second-order partial derivation details of the objective function of (10) can be computed as in (45) and (46), respectively.

$$\nabla_{a} \eta \left( {a,N} \right)\,{ = }\,\frac{{A_{1} A_{2} \left( {\varphi (N) - a} \right)\sqrt {H(N)} }}{{2\sqrt {2\pi a} }}\exp \left( { - \frac{{\left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)^{2} }}{2}} \right) - \left( {A_{2} \left( {1 - Q\left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)} \right) + A_{3} } \right)$$

(45)

$$\begin{aligned} \nabla_{a}^{2} \eta \left( {a,N} \right) &\, { = } - \frac{{A_{1} A_{2} H(N)}}{{4a\sqrt {2\pi } }} \\ & \quad \times \left( {3\sqrt a + \frac{1}{H(N)\sqrt a } + \left( {\varphi (N) - a} \right)A_{1} \left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)} \right)\exp \left( { - \frac{{\left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)^{2} }}{2}} \right) \\ \end{aligned}$$

$$\left( {3\sqrt a + \frac{1}{H(N)\sqrt a } + \left( {\varphi (N) - a} \right)A_{1} \left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)} \right)\exp \left( { - \frac{{\left( {A_{0} + A_{1} \sqrt {aH(N)} } \right)^{2} }}{2}} \right)$$

(46)

Since $A_{1} > 0$,$A_{2} > 0$,$A_{3} > 0$ and $0 < Q(x) < 1$, from (45) we have

$$\mathop {\lim }\limits_{a \to 0} \nabla_{a} \eta (a,N) = \frac{{A_{1} A_{2} \varphi (N)\sqrt {H(N)} }}{{2\sqrt {2\pi a} }}\exp \left( { - \frac{{A_{0}^{2} }}{2}} \right) = + \infty$$

(47)

$$\mathop {\lim }\limits_{a \to \varphi (N)} \nabla_{a} \eta (a,N) = - \left( {A_{2} \left( {1 - Q\left( {A_{0} + A_{1} \sqrt {\varphi (N)H(N)} } \right)} \right) + A_{3} } \right) < 0$$

(48)

which indicates that there is $a_{0} \left( N \right) \in \left[ {0,\varphi \left( N \right)} \right]$ that makes $\nabla_{a} \eta \left( {a_{0} N),N} \right) = 0$,$a_{0} \left( N \right)$ is an extreme point of $\eta \left( {a,N} \right).$

Then we will prove that is also a maximal point. As $P_{f} = Q\left( {A_{0} + A_{1} \sqrt {aH\left( N \right)} } \right) \le \varepsilon \le 0.5$, we have

$A_{0} + A_{1} \sqrt {aH\left( N \right)} > 0,$ and thus from (46) we have $\nabla_{a}^{2} \eta \left( {a,N} \right) < 0$,indicating that $\eta \left( {a,N} \right)$ is a convex function. Hence,$a_{0} \left( N \right)$ is the maximal point of $\eta \left( {a,N} \right)$.