Abstract
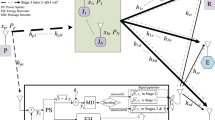
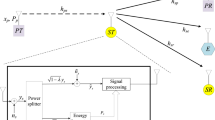
Overlay mechanism offers secondary users (SUs) chances to access licensed spectrum of primary users (PUs) to improve spectrum utilization efficiency. However, these chances impose serious security challenges when wire-tappers emulate legal users (SUs/PUs) to eavesdrop secret information. Moreover, energy sources available for SUs to transmit its private information as well as assist PUs in the overlay mechanism are problematic in green communication age. This paper proposes SUs who are able to scavenge radio frequency energy in signals of PUs to meet green communication requirement and jam wire-tappers to secure both secondary and primary information. Important secrecy performance indicators of overlay mechanism in radio frequency energy harvesting networks with jamming under Nakagami-m fading are evaluated by proposed precise expressions. Various results validate these expressions and show that secrecy performances of SUs and PUs are flexibly controlled, compromised and optimized with proper selections of system parameters as well as are dramatically affected by fading severity.










Similar content being viewed by others
Notes
The idea of this paper was conceived in our conference papers where we briefly presented a part of this paper for Rayleigh fading in [29] and Nakagami-m fading in [30]. However, we did not provide the detailed derivations of the performance expressions, various results, and thorough discussions on the results in both these conference papers. This paper presents the complete idea and derives elaborately the performance expressions as well as provides various results and discussions to obtain insights into the secrecy capability.
References
Ho, C. D., et al. (2021). Short-packet communications in wireless-powered cognitive IoT networks: Performance analysis and deep learning evaluation. IEEE Transactions on Vehicular Technology, 70(3), 2894–2899.
Askar, R., et al. (2021). Interference handling challenges toward full duplex evolution in 5G and beyond cellular networks. IEEE Wireless Communications, 28(1), 51–59.
Akhmetkaziyev, Y., et al. (2021). Performance of NOMA-enabled cognitive satellite-terrestrial networks with non-ideal system limitations. IEEE Access, 9, 35932–35946.
Tayel, A. F., et al. (2021). Throughput maximization of hybrid access in multi-class cognitive radio networks with energy harvesting. IEEE Transactions on Communications. https://doi.org/10.1109/TCOMM.2021.3059862.
Duy, T. T. et al. (2021). Outage Probability of Interference Cancellation Based Two-Way Relaying Cognitive Radio Protocol with Primary MIMO Communication, In Proc. IEEE ICCE, Phu Quoc Island, Vietnam, 13-15, pp. 481-486.
Albreem, M. A., et al. (2021). Green Internet of Things (GIoT): Applications, practices, awareness, and challenges. IEEE Access, 9, 38833–38858.
Shaikh, F. K., et al. (2016). Energy harvesting in wireless sensor networks: A comprehensive review. Renewable and Sustainable Energy Reviews, 55, 1041–1054.
Zeadally, S., et al. (2020). Design architectures for energy harvesting in the Internet of Things. Renewable and Sustainable Energy Reviews, 128, 1–22.
Wang, M., et al. (2021). Performance analysis of millimeter wave wireless power transfer with imperfect beam alignment. IEEE Transactions on Vehicular Technology, 70(3), 2605–2618.
Al-Obiedollah, H., et al. (2021). A joint beamforming and power-splitter optimization technique for SWIPT in MISO-NOMA system. IEEE Access, 9, 33018–33029.
Li, B., et al. (2021). Energy-efficient resources allocation with millimeter-wave massive MIMO in ultra dense HetNets by SWIPT and CoMP. IEEE Transactions on Wireless Communications. https://doi.org/10.1109/TWC.2021.3058776.
Song, K., et al. (2021). On the secrecy for relay-aided SWIPT internet of things system with cooperative eavesdroppers. IEEE Access, 9, 28204–28212.
Ho-Van, K., et al. (2020). Security enhancement for energy harvesting cognitive networks with relay selection. Wireless Communications and Mobile Computing. https://doi.org/10.1155/2020/8867148.
Ho-Van, K., et al. (2020). Security performance of underlay cognitive relaying networks with energy harvesting. Wireless Personal Communications, 110(2), 829–846.
Ho-Van, K., et al. (2020). Security analysis for underlay cognitive network with energy scavenging capable relay over Nakagami-m fading channels. Wireless Personal Communications, 110(2), 829–846.
Su, R. et al. (2019). Secure Cooperative Transmission in Cognitive AF Relay Systems with Destination-Aided Jamming and Energy Harvesting, In Proc. IEEE PIMRC, Istanbul, Turkey, 8-11 Sept. 2019, pp. 1-5
Su, R. et al. (2018). Destination-Assisted Jamming for Physical-Layer Security in SWIPT Cognitive Radio Systems, In Proc. IEEE WCNC, Barcelona, Spain, 15-18 April 2018, pp. 1-6.
Wang, D., et al. (2019). Primary privacy preserving with joint wireless power and information transfer for cognitive radio networks. IEEE Transactions on Cognitive Communications and Networking, 6(2), 683–693.
Xu, M. et al. (2018). Secure Transmission Solutions in Energy Harvesting Enabled Cooperative Cognitive Radio Networks, in Proc. IEEE WCNC, Barcelona, Spain, 15-18 April 2018, pp. 1-6.
Li, M., et al. (2018). Physical layer security in overlay cognitive radio networks with energy harvesting. IEEE Transactions on Vehicular Technology, 67(11), 11274–11279.
Khan, R., et al. (2020). A survey on security and privacy of 5G technologies: Potential solutions, recent advancements, and future directions. IEEE Communications Surveys and Tutorials, 22, 196–248.
Ebrahimi, N., et al. (2021). Physical layer secret key generation using joint interference and phase shift keying modulation. IEEE Transactions on Microwave Theory and Techniques. https://doi.org/10.1109/TMTT.2021.3058183.
Li, B., et al. (2021). Security enhancement with a hybrid cooperative NOMA scheme for MEC system’’. IEEE Transactions on Vehicular Technology. https://doi.org/10.1109/TVT.2021.3061718.
Alnagar, S. I., et al. (2021). Q-learning-based power allocation for secure wireless communication in UAV-aided relay network. IEEE Access, 9, 33169–33180.
Huang, K. W., et al. (2021). Jamming aided covert communication with multiple receivers. IEEE Transactions on Wireless Communications. https://doi.org/10.1109/TWC.2021.3059306.
Abughalwa, M., et al. (2021). A secrecy study of UAV based networks with fountain codes and FD jamming’’. IEEE Communications Letters. https://doi.org/10.1109/LCOMM.2021.3056389.
Sun, L., et al. (2020). Alternate-jamming-aided wireless physical-layer surveillance: Protocol design and performance analysis. IEEE Transactions on Information Forensics and Security, 16, 1989–2003.
Islam, S. H., et al. (2021). Impact of correlation and pointing error on secure outage performance over arbitrary correlated Nakagami-m and M-turbulent fading mixed RF-FSO channel. IEEE Photonics Journal, 13(2), 1–17.
Dang-Ngoc, H. et al. (2020). Key secrecy performance metrics of overlay networks with energy scavenging and artificial noise,” In Proc. IEEE SigTelCom, Ha Noi, Vietnam, 28-29 Aug. 2020, pp. 77-81.
Pham-Thi-Dan, N. et al. (2020) Secrecy throughput analysis of energy scavenging overlay networks with artificial noise,” In Proc. IEEE ATC, Khanh Hoa, Vietnam, 08-10 Oct. 2020, pp. 90-94.
Gradshteyn, I. S., et al. (2000). Table of integrals, series and products (6th ed.). San Diego, CA: Academic.
Wang, F., et al. (2020). Secure resource allocation for polarization-based non-linear energy harvesting over 5G cooperative CRNs’’. IEEE Wireless Communications Letters. https://doi.org/10.1109/LWC.2020.3028585.
Acknowledgements
This research is funded by Vietnam National University HoChiMinh City (VNU-HCM) under grant number C2020-20-27.
We would like to thank Ho Chi Minh City University of Technology (HCMUT), VNU-HCM for the support of time and facilities for this study.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Special Pdfs
Let
and
where U, \(J_{cw}\), and \(J_{cb}\) are defined in (29), (30), and (33), respectively.
This appendix derives the pdfs of \({Z_{cb}}\) and \({Z_{cw}}\).
From (74), one obtains
Because \(g_{cb} \ge 0\), \({Z_{cb}}\) is constrained in \(\left[ {\left. {1,\frac{U}{{{J_{cb}}}} + 1} \right) } \right. \).
The Jacobian coefficient is computed as
Given the variable transform in (74), the pdf of \(Z_{cb}\) can be obtained from the pdf of \(g_{cb}\) and the Jacobian coefficient as
Substituting \({f_{{g_{cb}}}}\left( z \right) = \frac{{\xi _{cb}^{{\alpha _{cb}}}}}{{\Gamma \left( {{\alpha _{cb}}} \right) }}{z^{{\alpha _{cb}} - 1}}{e^{ - {\xi _{cb}}z}}\) and the Jacobian coefficient into (78), the pdf of \(Z_{cb}\) is obtained as
where \(L_{cb}\), \(Q_{cb}\), and \(W_{cb}\) in (34), (36), and (39), respectively.
Similarly, the pdf of \(Z_{cw}\) is represented as
where \(L_{cw}\), \(Q_{cw}\), and \(W_{cw}\) in (31), (41), and (42), respectively.
Appendix B: Special Integral
This appendix solves the following integral
where \({S_{cb}} = \left\{ {U,J_{cb},{\xi _{cb}},{\alpha _{cb}},{\epsilon _b}} \right\} \) denotes the set of parameters related to the \(\texttt {C}\rightarrow \texttt {B}\) transmission and \(1 \le m < n \le L_{cb}\).
Inserting \({{f_{Z_{cb}}}\left( z \right) }\) in (79) into (81) and after changing the variable, (81) is rewritten as
Executing the binomial expansion to \({{{\left( {t + \frac{{{J_{cb}}}}{U}} \right) }^{{\alpha _{cb}} - 1}}}\) and after some simplifications, (82) is reduced to
By invoking [31, eq. (2.321.2)], the last integral in (83) is computed in closed-form, reducing (83) to
where
Appendix C: Proof of Lemma 1
Substituting \({{\hat{C}_a}}\) in (22) into \(\Delta \) in (25), one obtains
where K is defined in (32).
Invoking (14) and (17) for the case of \({{C_c} \ge {\bar{C}}}\), (86) is rewritten as
where \(Z_{cb}\) and \(Z_{cw}\) are defined in (74) and (75), correspondingly.
Due to statistical independence of \(Z_{cb}\) in (74) and \(Z_{cw}\) in (75), their joint pdf is the product of their individual pdfs. Consequently, \(\Delta \) in (87) can be computed as
Since \(f_{Z_{cb}}\left( z\right) \) in (79) is non-zero for \(z \in [1, L_{cb})\), the double integral in (88) can be solved by considering three cases of Kt in correlation to \([1, L_{cb})\): (Case 1: \(Kt < 1\)), (Case 2: \(1 \le Kt < L_{cb}\)), (Case 3: \(Kt > L_{cb}\)). “Case 1” means \(t< K^{-1} < 1\) and hence, \(\Delta \) for this case is \(\int \limits _{t < {K^{ - 1}}} {\left[ {\int \limits _0^{Kt} {{f_{{Z_{cb}}}}\left( z \right) dz} } \right] {f_{{Z_{cw}}}}\left( t \right) dt}=0\) because \({{f_{{Z_{cw}}}}\left( t \right) }\) in (80) is zero for \(t < 1\). Meanwhile, “Case 2” and “Case 3” respectively mean \(K^{-1} \le t<V\) and \(t>V\) where V is given in (35). Therefore, (88) is rewritten for “Case 2” and “Case 3” as
Since \({{f_{{Z_{cw}}}}\left( t \right) }\) is non-zero for \(t \in [1, L_{cw})\), in order to determine integral limits for t in (89), one must consider whether V falls in \([1, L_{cw})\) or not. Consequently, three contexts for V are investigated as follows.
Context 1: \(L_{cw}<V\)
Under this context, the second term in (89) is zero since \({{f_{{Z_{cw}}}}\left( t \right) }=0\) as \(t=V>L_{cw}\). Consequently, (89) is simplified as
The inner integral in (90) is solved by using (81) and hence,
Because \(\int \limits _1^{{L_{cw}}} {{f_{{Z_{cw}}}}\left( t \right) dt}=1\), (91) is simplified to (40) where
Consequently, the next step of the proof is to prove that (92) coincides (44). To this end, inserting \({{f_{Z_{cw}}}\left( t \right) }\) in (80) into (92) and after some simplications, one reduces (92) to
Executing consecutive variable transforms (\({z = 1/\left( {t - L_{cw}} \right) }\) and then \({t = - z}\)), one simplifies (93) to
Performing the series expansion \({e^x} = \sum \limits _{n = 0}^\infty {\frac{{{x^n}}}{{n!}}}\) for the term \({e^{\frac{{v/{{\left( {{L_{cw}} - V} \right) }^2}}}{{t + 1/\left( {V - {L_{cw}}} \right) }}}}\) in (94) and then executing the binomial expansion, one achieves
Executing the variable change \(z = t + {\left( {V - L_{cw}} \right) ^{ - 1}}\) and performing the binomial expansion, one simplifies (95) to (44) where
with I being defined in (43). As such, the last step of the proof is to show that (96) coincides (45). To this end, the following notes should be paid attention. First, it is straightforward to solve the second integral in the last equality of (96). Second, the first integral has a common form as \(\mathcal {G}\left( {g,v,b} \right) = \int \limits _g^\infty {{t^{v - 1}}{e^{ - bt}}dt}\), which is analytically evaluated as (46) by invoking [31, eq. (3.381.3)]. Finally, the third integral has a general form as \(\mathcal {Y}\left( {v,g,n} \right) = \int \limits _v^\infty {\frac{{{e^{ - gt}}}}{{{t^{n + 1}}}}dt}\), which is also analytically evaluated as (47) by invoking [31, eq. (358.4)]. After solving these three integrals, (96) is simplified to (45), completing the proof of \(\Delta _1\).
Context 2: \(1\le V<L_{cw}\)
This condition reduces (89) to
Before solving (97), it should be reminded that \({{f_{{Z_{cb}}}}\left( z \right) }\) is non-zero for \(z\in \left[ 1, L_{cb}\right) \) and thus, \({\int \limits _{z = 1}^{{L_{cb}}} {{f_{{Z_{cb}}}}\left( z \right) dz} }=1\). Furthermore, \(\int \limits _1^{Kt} {{f_{{Z_{cb}}}}\left( z \right) dz}\) and \(\int \limits _V^{{L_{cw}}} {{f_{{Z_{cw}}}}\left( t \right) dt}\) are represented in closed-form as \(\mathcal{M}\left( {1,Kt,{S_{cb}}} \right) \) and \(\mathcal{M}\left( {V,{L_{cw}},{S_{cw}}} \right) \) according to (81), correspondingly, where \({S_{cb}} = \left\{ {U,{J_{cb}},{\xi _{cb}},{\alpha _{cb}},{\epsilon _b}} \right\} \) and \({S_{cw}} = \left\{ {U,{L_{cw}},{\xi _{cw}},{\alpha _{cw}},{\epsilon _w}} \right\} \) are the sets of parameters related to the \(\texttt {C}\rightarrow \texttt {B}\) and \(\texttt {C} \rightarrow \texttt {W}\) transmission. Accordingly, (97) is reduced to
Substituting \({\mathcal{M}\left( {1,Kt,{S_{cb}}} \right) }\) in (84) into (98) and after some manipulations, (98) is reduced to (48) where
Accordingly, the next step of the proof of \(\Delta _2\) is to prove that (99) is expressed as (49). To this end, inserting \({{f_{{Z_{cw}}}}\left( t \right) }\) in (80) into (99) and then executing consecutive variable transforms (\(z=1/\left( t-V\right) \) and then \(t=-z\)), one simplifies (99) to
Performing some similar (series and binomial expansions) manipulations as (92), one obtains (49) where
which is further decomposed into three sub-cases as
where O is defined in (51). Consequently, the last step of the proof of \(\Delta _2\) is to show that (102) is reduced to (50). To this end, the following notes are helpful. First, it is easy to solve the second integral in the last equality of (102). Second, the first and the third integrals are represented in terms of \(\mathcal {G}\left( \cdot ,\cdot ,\cdot \right) \) and \(\mathcal {Y}\left( \cdot ,\cdot ,\cdot \right) \) in (46) and (47), correspondingly. After solving these three integrals, one reduces (102) to (50), finishing the proof of \(\Delta _2\).
Context 3: \(V<1\)
This condition reduces (89) to
Since \({{f_{{Z_{cw}}}}\left( t \right) }=0\) for \(t=V<1\), the first term in (103) is zero. Moreover, \({{f_{{Z_{cb}}}}\left( z \right) }\) is non-zero for \(z\in \left[ 1,L_{cb}\right) \) and \({{f_{{Z_{cw}}}}\left( t \right) }\) is non-zero for \(t\in \left[ 1,L_{cw}\right) \) and therefore, the second term in (103) is one. Plugging these results into (103), one infers \(\Delta = 1\), which agrees with (28) for \(V<1\). This completes the proof of \(\Delta \) for \(V<1\).
By combining three above contexts, \(\Delta \) is proved to match (28), completing the proof of Lemma 1.
Appendix D: Proof of Lemma 2
Using (13) and (18) for the case of \({{C_c} \ge {\bar{C}}}\) to rewrite \(\Omega _1\) in (55) as
It is seen from (87) and (104) that \(\Delta \) and \(\Omega _1\) have the same form. Consequently, the precise closed-form expression of \(\Omega _1\) can be taken from that of \(\Delta \) with appropriate variable substitutions as shown in Lemma 2, completing the proof.
Appendix E: Proof of Lemma 3
Let \({Z_{cd}} = 1 + \bar{K}{g_{cd}}\) and \({{\bar{Z}}_{cw}} = 1 + \frac{{\bar{H}{g_{cw}}}}{{\bar{M}{g_{cw}} + {\epsilon _w}}}\) where \(\bar{K}\), \(\bar{H}\), and \(\bar{M}\) are presented in (61), (59), and (58), respectively. Given the variable change, the pdf of \(Z_{cd}\) is taken from the pdf of \(g_{cd}\), \({f_{{g_{cd}}}}\left( z \right) \), as
Moreover, the pdf of \({\bar{Z}}_{cw}\) is given by
where \(\bar{U}\), \({{{\bar{Q}}_{cw}}}\) and \({{{\bar{W}}_{cw}}}\) are presented in (60), (63) and (64), respectively. Equation (106) is derived directly from the results in Appendix A.
Using (13) and (18) for the case of \({{C_c} < {\bar{C}}}\) to rewrite \(\Omega _2\) in (55) as
which is also expressed in terms of \(Z_{cd}\) and \({\bar{Z}}_{cw}\) as
Since \(Z_{cd}\) and \({\bar{Z}}_{cw}\) are statistically independent, (108) can be expressed in terms of the individual pdfs of \(Z_{cd}\) and \({\bar{Z}}_{cw}\) as
Since \({{f_{{Z_{cd}}}}\left( z \right) }\) is non-zero for \(z \ge 1\), the double integral in (109) can be solved by considering two cases of Kt in correlation to 1: (Case 1: \(Kt<1\)) and (Case 2: \(Kt>1\)). Therefore, (109) is rewritten in a compact form as
The first term in (110) is zero since \(\int \limits _{z < Kt} {{f_{{Z_{cd}}}}\left( z \right) dz} = 0\) owing to \({{f_{{Z_{cd}}}}\left( z \right) }=0\) for \(z=Kt < 1\). As such, by substituting (105) into the second term in (110) and after solving the inner integral in (110), one obtains
Executing the series expansion of \(\gamma \left( \cdot ,\cdot \right) \) in [31, eq. (8.352.1)] and then applying the binomial expansion, (111) reduces to
where \(\bar{J}\) is defined in (62).
Inserting \({{f_{{{\bar{Z}}_{cw}}}}\left( t \right) }\) in (106) into (112), one obtains
Executing the binomial expansion to reduce (113) to
where \(\bar{m}\) is defined in (65).
Applying the series expansion to \({e^{\bar{J}/x}}\), the last integral in (114) reduces to
Dependent on the difference between \(\bar{m}\) and u, \(\beta \) in (115) has different values
Three integrals in (116) are solved as follows. The second integral is easy to solve while the first and the third integrals are represented in terms of \(\mathcal {G}\left( \cdot ,\cdot ,\cdot \right) \) and \(\mathcal {Y}\left( \cdot ,\cdot ,\cdot \right) \) in (46) and (47), correspondingly. Given solutions of these three integrals, one reduces (116) to (66). Moreover, inserting (116) into (115), then plugging (115) into (114) and finally substituting (114) into (112), one reduces (112) to (57), finishing the proof of Lemma 3.
Rights and permissions
About this article
Cite this article
Dang-Ngoc, H., Ho-Van, K. & Do-Dac, T. Secrecy Analysis of Overlay Mechanism in Radio Frequency Energy Harvesting Networks with Jamming under Nakagami-m fading. Wireless Pers Commun 120, 447–479 (2021). https://doi.org/10.1007/s11277-021-08468-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-021-08468-2