Abstract
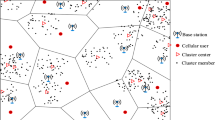
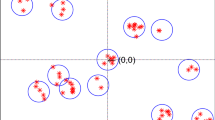
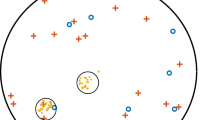
This paper studies the performance of device-to-device (D2D)-enabled cellular network with D2D users reusing downlink resources of cellular links. The cellular users and macro BSs are modeled as an independent Poisson point process (PPP), while the locations of D2D users are modeled as a Thomas cluster process. We analyze the performance of this D2D network for two cases: (1) the serving devices is selected uniformly at random from the same cluster, and (2) the serving devices is the closest devices to a typical device in the same cluster. We derive the theoretical expressions for the coverage probability, area spectral efficiency (ASE) and average rate of the whole network using stochastic geometry and analyze the performance trends with the number of simultaneously active D2D links per cluster, which shows that the closest choice case is better than the uniform choice case. The optimal number of simultaneously active D2D links per cluster can be obtained by analyzing ASE.






Similar content being viewed by others
References
Tehrani, M. N., Uysal, M., & Yanikomeroglu, H. (2014). Device-to-device communication in 5G cellular networks: challenges, solutions, and future directions. IEEE Communication Magazine, 52(5), 86–92.
Petsas., T et al. (2017). Measurement, modeling, and analysis of the mobile app ecosystem. ACM Transactions on Modeling & Performance Evaluation of Computing Systems, 2(2), 1–33.
Wang, H et al. (2017). A measurement study of device-to-device sharing in mobile social networks based on Spark. Concurrency and Computation: Practice and Experience, 29, 1–10.
4G Americas. (2015). 3GPP release 12 executive summary. Tech. Rep. https://www.scribd.com/doc/268610829/4G-Americas-3GPP-Release-12-Executive-Summary
Sakr, A. H., & Hossain, E. (2015). Cognitive and energy harvesting-based D2D communication in cellular networks: Stochastic geometry modeling and analysis. IEEE Trans on Communication, 63(5), 1867–1880.
Asadi, A., Wang, Q., & Mancuso, V. (2014). A survey on device-to-device communication in cellular networks. Communication Surveys Tuts, 16(4), 1801–1819.
Wyner, A. (1994). Shannon-theoretic approach to a Gaussian cellular multipleaccess channel. IEEE Transaction on Information Theory, 40(6), 1713–1727.
Andrews, J., Baccelli, F., & Ganti, R. (2011). A tractable approach to coverage and rate in cellular networks. IEEE Transactions on Communication, 59(11), 3122–3134.
Sun, H., Wildemeersch, M., Sheng, M., & Quek, T. Q. S. (2015). D2D enhanced heterogeneous cellular networks with dynamic TDD. IEEE Transaction on Wireless Communication, 14(8), 4204–4218.
Afshang, M., Dhillon, H. S., & Chong, P. H. J. (2016). Modeling and performance analysis of clustered device-to-device networks. IEEE Transaction on Wireless Communication, 15(7), 4957–4972.
M. Afshang and H. S. Dhillon, “Spatial modeling of device-to-device networks: Poisson cluster process meets poisson hole process,” in Proc., Asilomar, pp. 317–321, Nov, (2015).
Novlan, T. D., Dhillon, H. S., & Andrews, J. G. (2013). Analytical modeling of uplink cellular networks. IEEE Transaction on Wireless Communication, 12(6), 2669–2679.
Haenggi, M. (2012). Stochastic geometry for wireless networks. Cambridge Univ. Press.
Stoyan, D., Kendall, W. S., & Mecke, J. (1995). Stochastic Geometry and its Applications (2nd ed.). Wiley.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
Proof of (10)
Laplace transform of the interference at the typical D2D user from intra-cluster interfering D2D users, \(L_{{I_{{{\text{d2d}}}}^{{{\text{intra}}}} }} \left( {s|v_{0} } \right)\) is
where (a) represents the expectation of h∼exp(μ) and (b) represents the expectation of the number of interfering devices in each cluster, (c) under the assumption \(M > > m\), the formula is simplified based on the Taylor formula, and (d) follows from the change of variable \(\left\| {x_{0} + y} \right\| = r_{d1}\).
Proof of (12)
Laplace transform of the interference at the typical D2D user from inter-cluster interfering D2D users, \(L_{{I_{{{\text{d2d}}}}^{{{\text{inter}}}} }} \left( s \right)\) is
where (a) represents the expectation of h∼exp(μ) and (b) represents the expectation of the number of interfering devices in each cluster, (c) follows from the probability generating functional (PGFL) of PPP [14], (d) under the assumption \(M > > m\), the formula is simplified based on the Taylor formula, (e) follows from the change of variable \(\left\| {x + y} \right\| = r_{d2}\), (f) according to Taylor, the approximate \(1{\text{ - exp}}\left( { - ax} \right) \le a\) simplification formula is developed, and (g) follows by converting from Cartesian to polar coordinates where \(\int_{0}^{\infty } {\frac{1}{{1 + su^{ - \alpha } }}} f_{U} (u|v)du\).
Proof of (21)
Average rate of a typical D2D user for the uniform choice case, \(R_{{}}^{{\left( d \right)\left( {{\text{uniform}}} \right)}}\) is
where (a) represents the expectation of h∼exp(μ) and (b) follows from the change of variable \(s = \mu \left( {e^{t} - 1} \right) \, r_{c}^{\alpha } P_{d}^{ - 1}\).
Rights and permissions
About this article
Cite this article
Sun, Y., Zhu, L. Downlink Performance Analysis in D2D-Enabled Cellular Networks with Clustered Users. Wireless Pers Commun 122, 577–592 (2022). https://doi.org/10.1007/s11277-021-08913-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-021-08913-2