A NOMA-Enabled Cellular Symbiotic Radio for mMTC

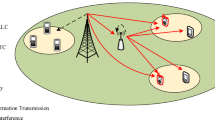
Abstract

Non-orthogonal multiple access (NOMA) scheme, potentially enabling high spectral efficiency, is one of the key technological innovations in the 5th generation (5G) cellular networks. The massive machine type communications (mMTC) service category of 5G supports ultra-dense deployment of connected devices with low-power and low data-rate requirements, and so it naturally supports internet-of-things (IoT) communications. Also, the ambient backscatter communications (BsC) holds potential for enabling energy-constrained IoT communications due to its extremely low power requirements. This work analyzes the downlink of a NOMA-enabled cellular system bundled with symbiotic radio-based mMTC. Closed-form expressions of the outage probability for the signal-to-interference and noise ratio (SINR) and the ergodic rate are derived for the symbiotic radio backscatter device as well as the primary cellular user. Several interesting use-cases of the proposed system model are discussed for future massive IoT and cell-free networks. The theoretical results presented are validated through numerical evaluations.

Appendices

Appendix A

If $f_{|h_{b_2}|^2}(h_{b_2}) = \frac{1}{\Gamma [m_{b_2}](\sigma _{b_2})^{m_{b_2}}}(h_{b_2})^{m_{b_2}-1}\exp {\Big [\frac{-h_{b_2}}{\sigma _{b_2}}}\Big ]$, and $f_{|h_w|^2}(h_w) = \frac{1}{\Gamma [m_{w}](\sigma _{w})^{m_{w}}}(w)^{m_{w}-1}\exp {\Big [\frac{-h_w}{\sigma _{w}}}\Big ]$, then $f_s(s)$ from (10) is evaluated as follows,

$$\begin{aligned} f_s(s)&{\mathop {=}\limits ^{(c)}}\int \limits _0^{+\infty } \frac{1}{w} \frac{(h_w)^{m_w-1}}{\Gamma [m_w](\sigma _{w})^{m_w}}\exp {\Big [\frac{-h_w}{\sigma _{w}}}\Big ] \frac{(\frac{s}{h_w})^{m_{b_2}-1}}{\Gamma [m_{b_2}](\sigma _{b_2})^{m_{b_2}}}\exp {\Big [\frac{-s}{h_w \sigma _{b_2}}}\Big ] \,\mathrm {d}h_w \\= & {} \frac{2 s^{m_{b_2}-1}\sigma _{b_2}^{-m_{b_2}}\sigma _w^{\frac{-m_w-m_{b_2}}{2}}}{\Gamma [m_{b_2}]\Gamma [m_w]}\left( \frac{\sigma _{b_2}}{s} \right) ^{\frac{m_{b_2}-m_w}{2}} K_{m_{b_2}-m_w}\left[ 2\sqrt{\frac{s}{\sigma _{b_2}\sigma _{w}}}\right] , \end{aligned}$$

where integral in (c) is evaluated using [37], and $K_{(\cdot )}[\cdot ]$ is a modified Bessel function of the second kind [39] valued as $K_{v}[z] = \int _0^{\infty } {\cos (t)}/{\left( t^2 + z^2 \right) ^{v+1/2}}\,\mathrm {d}t$.

Appendix B

If $f_{|h_{b_1}|^2}(h_{b_1}) = \frac{1}{\Gamma [m_{b_1}](\sigma _{b_1})^{m_{b_1}}}(h_{b_1})^{m_{b_1}-1}\exp {\Big [\frac{-h_{b_1}}{\sigma _{b_1}}}\Big ]$, then by adopting the same approach used to find $f_s(s)$ in Appendix A, the expression of $f_{\hat{s}}(\hat{s})$ can also be obtained as follows,

$$\begin{aligned} f_{\hat{s}}(\hat{s}) = \frac{2 \hat{s}^{m_{b_1}-1}\sigma _{b_1}^{-m_{b_1}}\sigma _w^{\frac{-m_w-m_{b_1}}{2}}}{\Gamma [m_{b_1}]\Gamma [m_w]}\left( \frac{\sigma _{b_1}}{\hat{s}} \right) ^{\frac{m_{b_1}-m_w}{2}} K_{m_{b_1}-m_w}\left[ 2\sqrt{\frac{\hat{s}}{\sigma _{b_1}\sigma _{w}}}\right] . \end{aligned}$$

Appendix C

The expression in (29) can be evaluated as follows,

$$\begin{aligned} F_{\Phi }(\phi ) = \mathrm {Pr}\left\{ |h_\mathrm {U1}|^2 < \frac{(p |\eta |^2 \hat{s} + \sigma _\circ ^2) \phi }{\alpha p} \right\} = 1 - \underbrace{\mathrm {Pr}\left\{ |h_\mathrm {U1}|^2 \ge \frac{(p |\eta |^2 \hat{s} + \sigma _\circ ^2) \phi }{\alpha p} \right\} }_{:=\Delta }, \end{aligned}$$

where $\Delta$ can be evaluated by adopting the same approach as used for evaluating (17). The final expression for $F_{\Phi }(\phi )$ can thus be written as follows,

$$\begin{aligned} F_{\Phi }(\phi )= & {} 1 - \frac{\exp { \left[ \frac{\phi \sigma _\circ ^2}{\sigma _1 \alpha p} \right] }}{\Gamma [m_{b_1}]\Gamma [m_w]} \left( -\frac{\sigma _{b_1}\sigma _{w}|\eta |^2 \phi }{\sigma _1 \alpha }\right) ^{-m_w-m_{b_1}} \Bigg \{ \left( - \frac{\sigma _{b_1}\sigma _{w}|\eta |^2 \phi }{\sigma _1 \alpha }\right) ^{m_w} \Gamma [m_{b_1}]\Gamma [m_w-m_{b_1}] \\&\times \, {_1F_1}\left( m_{b_1};1+m_{b_1}-m_{w};-\frac{\sigma _1 \alpha }{\sigma _{b_1}\sigma _{w}|\eta |^2\phi }\right) + \left( -\frac{\sigma _{b_1}\sigma _{w}|\eta |^2 \phi }{\sigma _1 \alpha }\right) ^{m_{b_1}} \Gamma [m_{w}]\Gamma [m_{b_1}-m_w] \\&\times \, {_1F_1}\left( m_{w};1-m_{b_1}+m_{w};-\frac{\sigma _1 \alpha }{\sigma _{b_1}\sigma _{w}|\eta |^2\phi }\right) \Bigg \}. \end{aligned}$$

Appendix D

By adopting the same approach as applied for obtaining $F_{\Phi }(\phi )$, the expression of $F_{\Theta }(\theta )$ used in (33) can also be evaluated, which is given as follows,

$$\begin{aligned} F_{\Theta }(\theta )= & {} 1-\frac{\exp { \left[ \frac{\theta \sigma _\circ ^2}{\sigma _2p(1-\alpha -\alpha \theta )} \right] }}{\Gamma [m_{b_2}]\Gamma [m_w]} \left( \frac{\sigma _{b_2}\sigma _{w}|\eta |^2 \theta }{\sigma _2(1-\alpha -\alpha \theta )}\right) ^{-m_w-m_{b_2}} \Bigg \{ \left( \frac{\sigma _{b_2}\sigma _{w}|\eta |^2 \theta }{\sigma _2(1-\alpha -\alpha \theta )}\right) ^{m_w} \\&\times \, \Gamma [m_{b_2}]\Gamma [m_w-m_{b_2}]{_1F_1}\left( m_{b_2};1+m_{b_2}-m_{w};\frac{\sigma _2(1-\alpha -\alpha \theta )}{\sigma _{b_2}\sigma _{w}|\eta |^2\theta }\right) + \left( \frac{\sigma _{b_2}\sigma _{w}|\eta |^2 \theta }{\sigma _2(1-\alpha -\alpha \theta )}\right) ^{m_{b_2}} \\&\times \, \Gamma [m_{w}]\Gamma [m_{b_2}-m_w]{_1F_1}\left( m_{w};1-m_{b_2}+m_{w};\frac{\sigma _2(1-\alpha -\alpha \theta )}{\sigma _{b_2}\sigma _{w}|\eta |^2\theta }\right) \Bigg \}. \end{aligned}$$

Appendix E

The parameter $\mathcal {Q}_1$ used in (36) can be expressed as follows,

$$\begin{aligned} \begin{array}{l} \displaystyle \mathcal {Q}_1 = \int _0^{\infty } (b)^{m_{b_1}-1} \exp {\left[ \frac{\sigma _\circ ^2}{p|\eta |^2 w b} - \frac{b}{\sigma _{b_1}} \right] } \mathrm {Ei}\left( -\frac{\sigma _\circ ^2}{p|\eta |^2 w b} \right) \,\mathrm {d}b. \end{array} \end{aligned}$$

By adapting the same approach used in (30), the expression for $\mathcal {Q}_1$ can be written as follows,

$$\begin{aligned} \mathcal {Q}_1= & {} \int \limits _0^{E} (b)^{m_{b_1}-1} \exp {\left[ \frac{\sigma _\circ ^2}{p|\eta |^2 w b} - \frac{b}{\sigma _{b_1}} \right] } \mathrm {Ei}\left( -\frac{\sigma _\circ ^2}{p|\eta |^2 w b} \right) \,\mathrm {d}b\\&{\mathop {\approx }\limits ^{(d)}}\frac{\pi E}{2n} \sum _{i=1}^{n} \sqrt{1-b_i^2} \left( \frac{E}{2} (b_i + 1) \right) ^{m_{b_1}-1} \exp {\left[ \frac{2 \sigma _\circ ^2}{p|\eta |^2 w (b_i + 1) E} - \frac{E (b_i + 1)}{2\sigma _{b_1}} \right] } \\&\times \,\mathrm {Ei}\left( \frac{-2 \sigma _\circ ^2}{p|\eta |^2 w (b_i + 1) E} \right) , \end{aligned}$$

where (d) represents the application of Gauss–Chebyshev quadrature method.