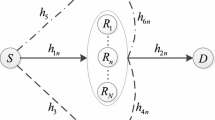
Abstract
Improving security and reliability is a main concern in many wireless transmission systems. In this paper, we explore the security and reliability in cognitive relay networks with an eavesdropper and multiple relays where the decode-and-forward (DF) protocol is considered. We propose a novel cognitive relay selection to improve the security and reliability of the considered system. The most important contribution is that we obtain the cumulative distribution functions (CDFs) of the channels from the selected relay to the destination and to the eavesdropper, respectively, which makes other related theoretical research possible. Furthermore, based on the proposed relay selection criterion, we derive the accurate closed-form outage probability and intercept probability of the considered system. At last, simulation results verify the correctness of our derivations. Interestingly, although the relay selection is based on the relay-destination channel and the relay-eavesdropper channel, it can be seen from the theoretical results that the reliability performance is completely irrelevant to the relay-eavesdropper channel’s statistical characteristics, whereas the security performance is entirely independent of statistical characteristics of the relay-destination channel. In addition, the security performance is always improved with the increasing number of relays, but the reliability performance is not proportional to the number of relays any more when the number of relays reaches a certain value.






Similar content being viewed by others
References
Zheng, L., & Tse, D. N. C. (2003). Diversity and multiplexing: a fundamental tradeoff in multiple-antenna channels. IEEE Transactions on Information Theory, 49(5), 1073–1096.
Akyildiz, I. F., Lee, W. Y., Vuran, M. C., & Mohanty, S. (2008). A survey on spectrum management in cognitive radio networks. IEEE Communications Magazine, 46(4), 40–48.
Sendonaris, A., Erkip, E., & Aazhang, B. (2003). User cooperation diversity. Part I. System description. IEEE Transactions on Communications, 51(11), 1927–1938.
Laneman, J. N., Tse, D. N. C., & Wornell, G. W. (2004). Cooperative diversity in wireless networks: Efficient protocols and outage behavior. IEEE Transactions on Information Theory, 50(12), 3062–3080.
Bletsas, A., Khisti, A., Reed, D. P., & Lippman, A. (2006). A simple cooperative diversity method based on network path selection. IEEE Journal on Selected Areas in Communications, 24(3), 659–672.
Bletsas, A., Shin, H., & Win, M. Z. (2007). Cooperative communications with outage-optimal opportunistic relaying. IEEE Transactions on Wireless Communications, 6(9), 3450–3460.
Li, E., Wang, X., Dong, Y., & Li, Y. (2016). Research on the \(N\)th-best relay selection with outdated feedback in selection cooperation systems. Wireless Personal Communications, 89(1), 45–59.
Rankov, B., & Wittneben, A. (2007). Spectral efficient protocols for half-duplex fading relay channels. IEEE Journal on Selected Areas in Communications, 25(2), 379–389.
Li, E. Y., & Yang, S. Z. (2012). Simple relay selection criterion for general two-way opportunistic relaying networks. Electronics Letters, 48(14), 881–882.
Yucek, T., & Arslan, H. (2009). A survey of spectrum sensing algorithms for cognitive radio applications. IEEE Communications Surveys and Tutorials, 11(1), 116–130.
Axell, E., Leus, G., Larsson, E. G., & Poor, H. V. (2012). Spectrum sensing for cognitive radio: State-of-the-art and recent advances. IEEE Signal Processing Magazine, 29(3), 101–116.
Letaief, K. B., & Zhang, W. (2009). Cooperative communications for cognitive radio networks. Proceedings of the IEEE, 97(5), 878–893.
Zhong, B., & Zhang, Z. (2016). Opportunistic two-way full-duplex relay selection in underlay cognitive networks. IEEE Systems Journal, 64(10), 1–10.
Yang, H., Pandharipande, A., & Ting, S. H. (2009). Cooperative decode-and-forward relaying for secondary spectrum access. IEEE Transactions on Wireless Communications, 8(10), 4945–4950.
Lee, J., Wang, H., Andrews, J. G., & Hong, D. (2011). Outage probability of cognitive relay networks with interference constraints. IEEE Transactions on Wireless Communications, 10(2), 390–395.
Li, D. (2016). Amplify-and-forward relay sharing for both primary and cognitive users. IEEE Transactions on Vehicular Technology, 65(4), 2796–2801.
Li, Q., & Varshney, P. K. (2017). Resource allocation and outage analysis for an adaptive cognitive two-way relay network. IEEE Transactions on Wireless Communications, 16(7), 4727–4737.
Leung-Yan-Cheong, S., & Hellman, M. (1978). The Gaussian wire-tap channel. IEEE Transactions on Information Theory, 24(4), 451–456.
Lai, L., & Gamal, H. E. (2008). The relay-eavesdropper channel: Cooperation for secrecy. IEEE Transactions on Information Theory, 54(9), 4005–4019.
Krikidis, I. (2010). Opportunistic relay selection for cooperative networks with secrecy constraints. IET Communications, 4(15), 1787–1791.
Zou, Y., Wang, X., & Shen, W. (2013). Optimal relay selection for physical-layer security in cooperative wireless networks. IEEE Journal on Selected Areas in Communications, 31(10), 2099–2111.
Chen, J., Zhang, R., Song, L., Han, Z., & Jiao, B. (2012). Joint relay and jammer selection for secure two-way relay networks. IEEE Transactions on Information Forensics and Security, 7(1), 310–320.
Hoang, T. M., Duong, T. Q., Vo, N.-S., & Kundu, C. (2017). Physical layer security in cooperative energy harvesting networks with a friendly jammer. IEEE Wireless Communications Letters, 6(2), 174–177.
Chu, S.-I. (2019). Secrecy analysis of modify-and-forward relaying with relay selection. IEEE Transactions on Information Theory, 68(2), 1796–1809.
Feng, Y., Yan, S., Liu, C., Yang, Z., & Yang, N. (2019). Two-stage relay selection for enhancing physical layer security in non-orthogonal multiple access. IEEE Transactions on Information Forensics and Security, 14(6), 1670–1683.
Lei, H., Yang, Z., Paik, K.-H., Ansari, I. S., Guo, Y., Pan, G., & Alouini, M.-S. (2019). Secrecy outage analysis for cooperative NOMA systems with relay selection schemes. IEEE Transactions on Communications, 67(9), 6282–6298.
Wang, Z., & Peng, Z. (2019). Secrecy performance analysis of relay selection in cooperative NOMA systems. IEEE Access, 7, 86274–86287.
Li, J., Han, S., Tai, X., Gao, C., & Zhang, Q. (2020). Physical layer security enhancement for satellite communication among similar channels: Relay selection and power allocation. IEEE Systems Journal, 14(1), 433–444.
Wang, Y., Yin, H., Yang, W., Zhang, T., Shen, Y., & Zhu, H. (2020). Secure wireless powered cooperative communication networks with finite energy storage. IEEE Transactions on Vehicular Technology, 69(1), 1008–1022.
Zhang, G., Gao, Y., Luo, H., Wang, S., Guo, M., & Sha, N. (2020). Security performance analysis for best relay selection in energy-harvesting cooperative communication networks. IEEE Access, 8, 26–36.
Mabrouk, A., Tourki, K., Shafie, A. . El., & Al-Dhahir, N. (2020). Relay-selection refinement scheme for secrecy in untrusted RF-EH relay systems with adaptive transmission under outdated CSI. IEEE Transactions on Green Communications and Networking, 4(2), 423–432.
Liu, Y., Wang, L., Duy, T. T., Elkashlan, M., & Duong, T. Q. (2015). Relay selection for security enhancement in cognitive relay networks. IEEE Wireless Communications Letter, 4(1), 46–49.
Ding, X., Song, T., Zou, Y., & Chen, X. (2016). Relay selection for secrecy improvement in cognitive amplify-and-forward relay networks against multiple eavesdroppers. IET Communications, 10(15), 2043–2053.
Zou, Y., Champagne, B., Zhu, W. P., & Hanzo, L. (2015). Relay-selection improves the security-reliability trade-off in cognitive radio systems. IEEE Transactions on Communications, 63(1), 215–228.
Xu, X., Yang, W., & Cai, Y. (2017). Opportunistic relay selection improves reliability-reliability tradeoff and security-reliability tradeoff in random cognitive radio networks. IET Communications, 11(3), 335–343.
Yan, P., Zou, Y., Ding, X., & Zhu, J. (2020). Energy-aware relay selection improves security-reliability tradeoff in energy harvesting cooperative cognitive radio systems. IEEE Transactions on Vehicular Technology, 69(5), 5115–5128.
Cao, Z., Ji, X., Wang, J., Zhang, S., Ji, Y., & Wang, J. (2019). Security-reliability tradeoff analysis for underlay cognitive two-way relay networks. IEEE Transactions on Wireless Communications, 18(12), 6030–6042.
Ji, B., Li, Y., Cao, D., Li, C., Mumtaz, S., & Wang, D. (2020). Secrecy performance analysis of UAV assisted relay transmission for cognitive network with energy harvesting. IEEE Transactions on Vehicular Technology, 69(7), 7404–7415.
Acknowledgements
he authors would like to thank the editors and the anonymous reviewers for their constructive comments and suggestions, which helped to improve the quality of this paper. This work was supported by Shandong Provincial Natural Science Foundation, China under Grant Nos. ZR2018MF002 and ZR2020MF001, Teaching & Research Program under Grant No. F2018-052-3, National Undergraduate Innovation and Entrepreneurship Training Program under Grant No. S202010429191, National Natural Science Foundation of China under Grant No. 61701272.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1
When \(j \ge 1\), the result of \(G\left( {z,j} \right)\) is derived as follows:
Appendix 2
Let \({\gamma _k} = {{{\gamma _{kD}}} /{{\gamma _{kE}}}}\), the PDF \({\gamma _{{k^{\mathrm{*}}}D}}\) can be obtained by
The CDF of \({\gamma _k}\) can be expressed as
By taking the derivative of (39), we have
According to (7), we can also get the CDF of \({\gamma _{{k^*}}} =\mathop {\max }\limits _{k \in {\mathbf{D}}} \left\{ {{{{\gamma _{kD}}} / {{\gamma _{kE}}}}} \right\}\) as
Taking the derivative of (41), we obtain the corresponding PDF of \({\gamma _{{k^*}}}\) as follows:
Thus, the joint CDF \({F_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right)\) is derived as
Therefore, after taking the derivative of (43), we get the joint PDF \({f_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right)\) as follows:
By substituting (40), (42) and (44) into (38), we get
The final closed-form result of \({f_{{\gamma _{{k^{*}}D}}}} \left( x\right)\) is not used in the subsequent derivation process, so we needn’t give the final closed-form expression of \({f_{{\gamma _{{k^{*}}D}}}}\left( x\right)\).
Substituting (40), (42) and (44) into (38), meanwhile, we integrate the PDF of \(\gamma _{{k^{*}}D}\), then the final result of the CDF of \(\gamma _{{k^{*}}D}\) is derived as (46).
Appendix 3
The joint CDF \({F_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right)\) is derived as
Therefore, after taking the derivative of (47), we get the joint PDF \({f_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right)\) as
Therefore, the expression of \({f_{{\gamma _{{k^{*}}E}}}}(x)\) is derived as
The CDF of \({\gamma _{{k^{*}}E}}\) can be derived as (50).
Appendix 4
Appendix 5
By using of (45), the term \(\Pr \left\{ {\frac{{{\gamma _{{k^*}D}}}}{{{\gamma _{PD}} + 1}} < T} \right\}\) can be derived as follows:
where
Appendix 6
By using of (49), the term \(\Pr \left\{ {\frac{{{\gamma _{{k^*}E}}}}{{{\gamma _{PE}} + 1}} > T} \right\}\) can be derived as follows:
Rights and permissions
About this article
Cite this article
Li, E., Ma, L., Hao, S. et al. Security and Reliability Analysis of Relay Selection in Cognitive Relay Networks. Wireless Pers Commun 123, 3103–3125 (2022). https://doi.org/10.1007/s11277-021-09279-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11277-021-09279-1