Analysis of a Low Cost and Low Complexity Adaptive Transmission Scheme for Massive MIMO Systems with Interference

Abstract

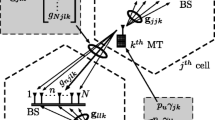
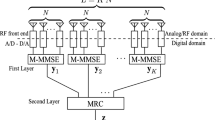
This paper evaluates a low-complexity Multiuser Adaptive Modulation (MAM) scheme for an uplink massive multiple-input and multiple-output (MIMO) systems with maximum-ratio combining (MRC) linear receivers, which requires only slow-varying large-scale shadowing information for the users. For a channel that includes both small-scale and large-scale fading, the probability density function of signal-to-interference-plus-noise ratio (SINR) is mathematically analyzed and verified by simulation. Furthermore, closed-form expressions are derived for the average spectral efficiency and bit error outage. Since the MRC is desirable in low transmit power, the obtained analytical expressions are approximated at low power levels. Moreover, the paper investigates different users’ arrangements around the base station to achieve the maximum possible bit rate. For MAM with joint power control, optimal power adaptation strategy switching thresholds are also acquired. Compared to the existing research literature, the proposed adaptive scheme by the MRC receiver gives similar performance as a proper adaptive method at low power transmission.

Appendices

Appendix A

1.1 Proof Theorem I

In this appendix, we evaluate the conditional PDF of SINR on ${\overline{\gamma }}_{k}$ for the channel state in case I.

Instantaneous SINR of user k for the channel state in case I will be as below:

$${\gamma }_{k}=\frac{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}}{\sum_{\begin{array}{c}i=1\\ i \ne k\end{array}}^{K}\frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}} + \frac{1}{\beta p}}$$

(42)

$${\gamma }_{k}=\frac{ X}{\sum_{\begin{array}{c}i=1,\ne k\\ \end{array}}^{K} {z }_{ik} + \frac{M}{{\overline{\gamma }}_{k}}}$$

(43)

Then:

$${\mathrm{X }= {\Vert {\mathbf{h}}_{\mathrm{k}}\Vert }^{2},\mathrm{ z }}_{ik}=\frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}}$$

(44)

where:

$$Z=\sum_{\begin{array}{c}i=1\\ i \ne k\end{array}}^{K} {z }_{ik} , Z \sim G\left(K-1 ,1\right) ,X \sim G\left(M,1\right)$$

(45)

$$T = Z + \frac{M}{\overline{\gamma }}$$

(46)

where in Eq. (46), $T$ has a three-parameter (shifted) gamma distribution$G\left(K-1 , 1 , \frac{M}{\overline{\gamma }}\right)$.

By Jacobian Method (${\gamma }_{k}= \frac{\mathrm{X}}{\mathrm{T}}$, T = T;${f}_{{\Upsilon}_{k} , T}\left({\gamma }_{k},t\right)={\left|\mathrm{J}\right|}^{-1} {f}_{X , T}\left(x,t\right)$):

$${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)= \underset{-\infty }{\overset{+\infty }{\int }}{f}_{{\Upsilon}_{k} , T}\left({\gamma }_{k},t\right)dt= \frac{{\gamma }^{M-1}{e}^{\frac{M}{\overline{\gamma }}}}{\Gamma (M)\Gamma (K-1)}\underset{\frac{M}{\overline{\gamma }}}{\overset{\infty }{\int }}{t}^{M}{e}^{-(\gamma +1)t}{ (t-\frac{M}{\overline{\gamma }} )}^{K-2} dt$$

(47)

This integral can be solved using equation [22, (3.383–4)]:

$${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)= \frac{{\gamma }^{M-1}{e}^{\frac{-M\gamma +M}{2\overline{\gamma }}}}{\Gamma \left(M\right){\left(\frac{\overline{\gamma }}{M}\right)}^{\frac{M+K-2}{2}}{\left(\gamma +1\right)}^{\frac{M+K}{2}}} \times {W}_{\frac{M-K+2}{2} , \frac{1-M-K}{2} }(\frac{M}{\overline{\gamma }}(\gamma +1))={\left(-1\right)}^{M}\frac{M{e}^{\frac{-M\gamma }{\overline{\gamma }}}{\gamma }^{M-1}}{{\left(\gamma + 1\right)}^{ M+K-1}}{ L}_{M}^{\left(1-K-M\right)}\left(\frac{M}{\overline{\gamma }}\left(\gamma +1\right)\right)$$

(48)

where ${L}_{n}^{\alpha }$ is [22, (8.970.1)]:

$${L}_{n}^{\alpha }(x)=\sum_{i=0}^{n}{(-1)}^{n}\left(\genfrac{}{}{0pt}{}{n+\alpha }{n-i}\right)\frac{{x}^{i}}{i!}$$

(49)

$${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)=M\sum_{i=0}^{M}{(-1)}^{i} {e}^{\frac{-M\gamma }{\overline{\gamma }}}{\gamma }^{M-1}\left(\genfrac{}{}{0pt}{}{\rho }{M-i}\right)\frac{{\left(\gamma + 1\right)}^{ i-M-K+1}}{{(\frac{\overline{\gamma }}{M})}^{i} i!}$$

(50)

where ρ $=1-K$ (Fig. 9, 10, 11).

Fig. 9

${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)$ for case I, M = 2048, K = 5 and $\overline{\gamma }=10$, $p=0~dB$

Appendix B

2.1 Proof Theorem 2

In this appendix, we evaluate the conditional PDF of SINR on ${\overline{\gamma }}_{k}$ for the channel state in case II.

Instantaneous SINR of user k for the channel state in case II will be as below:

$${\gamma }_{k}=\frac{p {\beta }_{k} {\Vert {\mathbf{h}}_{k}\Vert }^{2}}{p\sum_{\begin{array}{c}i=1\\ i \ne k\end{array}}^{K}{\beta }_{i} \frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{{\Vert {\mathbf{h}}_{k}\Vert }^{2}} + 1}$$

(51)

$${\gamma }_{k}=\frac{{\overline{\gamma }}_{k}}{M}\frac{ X}{p\sum_{\begin{array}{c}i=1\\ i \ne k\end{array}}^{K} {z}_{ik} + 1}$$

(52)

$${X=\Vert {\mathbf{h}}_{\mathrm{k}}\Vert }^{2},{{z}_{ik}=\beta }_{i}\frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}}$$

(53)

As we know:

$${\beta }_{i} \sim G\left(a ,\theta \right), \frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}}\sim \mathrm{exp}\left(1\right)$$

(54)

$${z}_{ik} \sim {K}_{distribution } (a\mathrm{\theta }, a , 1)$$

(55)

where the relation in (55) implies that ${z}_{ik}$ follows a $K$-distribution with the mean of $a\theta$ and the first and second shape parameters, $a$ and 1, respectively. Also, the definition of parameter $\theta$ is as follows:

$$\theta =\frac{b}{{d}^{v}}$$

(56)

$${d}^{v}={(r/{r}_{h})}^{v}, r={r}_{k} , k=1,\dots ,K$$

(57)

If we consider $Z$ as the sum of ${z}_{ik}$ random variables, then:

$$Z=\sum_{\begin{array}{c}i=1\\ i \ne k\end{array}}^{K}{z}_{ik}$$

(58)

It is proven in [23] that the sum of $K$- distributed random variables follows a $K$- distributed random variable with a different shape factor. Therefore, $Z\sim {K}_{distribution }\left(\theta \left(K-1\right) a, a , K-1\right)$ and the distribution of random variable$Z$:

$${f}_{Z}\left(z\right)=\frac{2}{{\theta }^{\frac{a+K-1}{2}}\Gamma \left(K-1\right)\Gamma \left(a\right)}\times {z}^{\frac{a+K-1}{2} - 1} {K}_{a-K+1}\left(2\sqrt{\frac{z}{\theta }}\right)$$

(59)

Then, we assume $T=pZ+1$. Therefore, $T$ has a four-parameter (shifted) K-distribution,

${K}_{distribution }\left(p\theta \left(K-1\right) a, a , K-1, 1\right)$ with PDF given by:

$${f}_{T}\left(t\right)=\frac{2}{{\left(p\theta \right)}^{\frac{a+K-1}{2}}\Gamma \left(K-1\right)\Gamma \left(a\right)}\times {(t-1 )}^{\frac{a+K-1}{2}-1} {K}_{a-K+1}\left(2\sqrt{\frac{t-1}{p\theta }}\right)$$

(60)

By Jacobian Method like previous part$(\Psi = \frac{\mathrm{X}}{\mathrm{T}} )$, we have:

$${f}_{\Psi }\left(\psi \right)=\frac{2{\psi }^{M-1}}{{\left(p\theta \right)}^{\frac{a+K-1}{2}}\Gamma \left(M\right)\Gamma \left(K-1\right)\Gamma \left(a\right)}\times \underset{1}{\overset{\infty }{\int }}{t}^{M}{e}^{-\psi t}{ (t-1 )}^{\frac{a+K-3}{2}} {K}_{a-K+1}\left(2\sqrt{\frac{t-1}{p\theta }}\right) dt$$

(61)

If we put:

$$I =\underset{1}{\overset{\infty }{\int }}{t}^{M}{e}^{-\psi t}{ (t-1 )}^{\frac{a+K-3}{2}} {K}_{a-K+1}\left(2\sqrt{\frac{t-1}{p\theta }}\right) dt$$

(62)

Then by changing of variable ${\varphi = (t-1 )}^\frac{1}{2}$ eventually, we have:

$$I=2{e}^{-\psi }\sum_{i=0}^{M}\left(\genfrac{}{}{0pt}{}{M}{i}\right)\underset{0}{\overset{\infty }{\int }}{\varphi }^{K+a-2+2i} {e}^{-\psi {\varphi }^{2}} {K}_{a-K+1}\left(\frac{2\varphi }{\sqrt{p\theta }}\right)d\varphi$$

(63)

This integral is solved using equation [22, (6.631–3)]:

$$I = \frac{\sqrt{p\theta }}{2}\mathit{exp}\left(\frac{1}{2p\theta \psi }- \psi \right)\left(\sum_{i=0}^{M}\left(\genfrac{}{}{0pt}{}{M}{i}\right){\psi }^{- \frac{1}{2}\left(K+a-2+2i\right)} \times \Gamma \left(a+i\right)\Gamma \left(K-1+i\right)\times {W}_{- \frac{1}{2}\left(K+a-2+2i\right) , \frac{1}{2}\left(a-K+1\right) }\left(\frac{1}{p\theta \psi }\right)\right)$$

(64)

Finally, the PDF is as follows:

(65)

where:

(66)

Fig. 10

${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)$ for case II, M = 2048, K = 5 and $\overline{\gamma }=10 dB$, $p=0 dB$

Appendix C

3.1 Proof Theorem 3

In this appendix, we evaluate the conditional PDF of SINR on ${\overline{\gamma }}_{k}$ for the channel state in case III.

Reconsidering Eq. (52) for the channel state in case III, we have:

$${X=\Vert {{\varvec{h}}}_{k}\Vert }^{2},{z }_{ik}= {\beta }_{i}{y}_{ik}$$

(67)

As we know:

$${\beta }_{i} \sim G\left(a , {\theta }_{i}\right)$$

(68)

$${y}_{k}={y}_{ik}=\frac{{\left|{{\mathbf{h}}_{k}}^{H}{\mathbf{h}}_{i}\right|}^{2}}{ {\Vert {\mathbf{h}}_{k}\Vert }^{2}}\sim \mathrm{exp}(1)$$

(69)

where omitting index $i$ in (69) can be asymptotically true only for a small number of users ($K$).

As we know:

$$\theta _{i} = \frac{b}{{d_{i} ^{v} }},d_{i} ^{v} = \left( { r_{i} / r_{h} } \right)^{{v}}$$

(70)

By fixing ${\beta }_{i}$ and writing ${y}_{k}{ =z }_{ik}/{\beta }_{i}$, we obtain the conditional PDF ${f}_{{z }_{ik}|{y}_{k}}\left(z|y\right)$ as follows:

$${f}_{{z }_{ik}|{y}_{k}}\left(z|y\right)= \frac{{z}^{a-1}}{\Gamma (a){{(y\theta }_{i})}^{a}} {e}^{-\frac{z}{{y\theta }_{i}}}$$

(71)

So, the distribution for the RV ${z }_{ik}$ can be described as:

$${f}_{{z }_{ik}}\left(z\right)= {E}_{y}\left[{f}_{{z }_{ik}|{y}_{k}}\left(z|y\right)\right]$$

(72)

Considering (72), each ${z }_{ik}$ can be viewed as a Gamma-distributed RV with shape parameter $a$, and random scale parameter ${y\theta }_{i}$. It follows that given ${y}_{k}$, the RV $Z$ in (58) is the sum of $K-1$ independent gamma-distributed RVs with different second parameters. Finally, the PDF of $Z$ conditioned on ${y}_{k}$ can be computed by Satterthwaite Procedure. This procedure is described in lemma 1.

Lemma 1: $\frac{\nu U}{E\left\{U\right\}}$ has an approximate ${\chi }^{2}$ distribution with the following degree of freedom:

$$\nu =\frac{{\left(\sum_{i=1}^{k}{a}_{i}E\left\{{U}_{i}\right\}\right)}^{2}}{\sum_{i=1}^{k}{({a}_{i}E\left\{{U}_{i}\right\})}^{2}/{\nu }_{i}}$$

(73)

We can assume ${X}_{i}= {{a}_{i}U}_{i} \sim G({ K}_{i} , {\eta }_{i})$ where ${K}_{i}= {\nu }_{i}/2$ and ${\eta }_{i}=$ 2${a}_{i}$.

$$X= \sum_{i}{X}_{i} ; \frac{\nu X}{E\left\{X\right\}} \sim \chi \left(\nu \right)$$

(74)

$$\nu = \frac{{\left(\sum_{i=1}^{k}{ K}_{i}{\eta }_{i}\right)}^{2}}{\sum_{i=1}^{k}{({ K}_{i}{\eta }_{i})}^{2}/{2K}_{i}} , E\left\{X\right\}= \sum_{i}{ K}_{i}{\eta }_{i}$$

(75)

Therefore, we have:

$$X \sim G( {K}_{sum} , { \eta }_{sum})$$

(76)

$${K}_{sum}= \frac{{\left(\sum_{i=1}^{k}{ K}_{i}{\eta }_{i}\right)}^{2}}{\sum_{i=1}^{k}{{ K}_{i}{\eta }_{i}}^{2}} , { \eta }_{sum}= \frac{\sum_{i=1}^{k}{{K}_{i}\eta }_{i}}{{K}_{sum}}$$

(77)

In our case, we replace ${K}_{i} with \ a$ for all $i$, ${\eta }_{i}= {y\theta }_{i}$ and also ${X}_{i}$ with conditional ${z}_{ik}$ on ${y}_{k}$ so we have approximated conditional pdf for $Z$ as bellow:

$$Z \sim G( {A}_{k} , y{B}_{k} )$$

(78)

where:

$${A}_{k}= a\frac{{\left(\sum_{i=k , i\ne k}^{K}{\theta }_{i}\right)}^{2}}{\sum_{i=k , i\ne k}^{K}{{\theta }_{i}}^{2}} , {B}_{k}= a\frac{\sum_{i=k , i\ne k}^{K}{\theta }_{i}}{{A}_{k}}$$

(79)

So, the unconditional distribution of Z can be obtained by averaging the PDF over ${y}_{k}$, that is:

$${f}_{Z}\left(Z\right)= \underset{0}{\overset{\infty }{\int }}{f}_{Z|y}\left(Z|y\right){f}_{y}\left(y\right)dy=\frac{{Z}^{{A}_{k}-1}}{\Gamma ({A}_{k}){{B}_{k}}^{{A}_{k}}}\underset{0}{\overset{\infty }{\int }}{y}^{-{A}_{k}}{e}^{-\left(y+\frac{Z}{y{B}_{k}}\right)}dy$$

(80)

Again, following the step from (60) to (64), we have:

$${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)\approx \frac{{\left(\frac{M}{\overline{\gamma }}\right)}^{M} {\gamma }^{M-1}\mathit{exp}\left(\frac{\overline{\gamma }}{2Mp{B}_{k}\gamma }- \frac{M}{\overline{\gamma }}\gamma \right)}{{\left(p{B}_{k}\right)}^{\frac{{A}_{k}}{2}}\Gamma \left(M\right)\Gamma \left({A}_{k}\right)}\left(\sum_{i=0}^{M}\left(\genfrac{}{}{0pt}{}{M}{i}\right){\left(\frac{M\gamma }{\overline{\gamma }}\right)}^{- \frac{1}{2}\left({A}_{k}+2i\right)}\Gamma \left({A}_{k}+i\right)\times \Gamma \left(i+1\right){W}_{- \frac{1}{2}\left({A}_{k}+2i\right) , \frac{1}{2}\left({A}_{k}-1\right) }\left(\frac{\overline{\gamma }}{Mp{B}_{k}\gamma }\right)\right)$$

(81)

Fig. 11

${f}_{{\Upsilon}_{k}|{\overline{\Upsilon} }_{k}}\left(\gamma |\overline{\gamma }\right)$ for case III, M = 2048, K = 5 and$\overline{\gamma }=10$, $p=0 dB$