Skip to main content

Advertisement

Springer Nature Link
Log in

Design of Energy Efficient Multiplier with Approximate Computing on Scalable Compressor for Error-Resilient Image Contrast Enhancement

  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

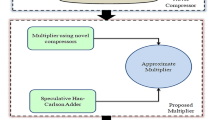
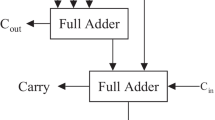
A number of arithmetic operations and applications use digital logic circuits as their primary building blocks, to operate with high reliability and precision. The multiplier is the core part of most arithmetic designs. The trend of imprecise multiplier has gained visibility in recent years, especially for image processing applications. Most of the multiplier designs use a compressor in the dot product reduction. In recent years, researchers have focused on designing imprecise, or approximate compressor to reduce design complexity while maintaining a low error rate. For higher bit multiplication, the design of a higher-order compressor is required. Using Karnaugh map (K-map) and truth table for approximation is a challenging task for the higher-order compressor. To address this issue, a scalable compressor with reasonable approximation using counter-based comparison methods is designed in this paper. The simulation results used with scalable compressors are compared with the existing 8 × 8 and 16 × 16 multipliers. These approximate circuits show significant improvement in the efficiency of multimedia signal processing, leading to better efficiency in terms of 30% area, 25% power, 20% delay, mean error distance (MED), error distance (ED), and normalized error distance (NED). The proposed method is applied in image multiplications for image contrast enhancement application. The peak signal-to-noise ratio (PSNR) is then determined and compared to other existing work.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Code Availability

Code will be made available upon request and over GitHub.

References

  1. Kuo, S. M., Lee, B. H., & Tian, W. (2013). Real-time digital signal processing: Fundamentals, implementations and applications. Wiley.

    Google Scholar 

  2. Dandapat, A., Ghosal, S., Sarkar, P., & Mukhopadhyay, D. (2010). A 1.2-ns 16 × 16-bit binary multiplier using high speed compressors. International Journal of Electrical and Electronics Engineering, 4(3), 234–239.

    Google Scholar 

  3. Parhi, K. K. (1999). VLSI digital signal processing systems: Design and implementation (1st ed.). Wiley.

    Google Scholar 

  4. Parhami, B. (2010). Computer arithmetic. Oxford University Press.

    Google Scholar 

  5. Mittal, S. (2016). A survey of techniques for approximate computing. ACM Computing Surveys (CSUR), 48(4), 1–33.

    Google Scholar 

  6. Gorantla, A., & Deepa, P. (2019). Design of approximate subtractors and dividers for error tolerant image processing applications. Journal of Electronic Testing, 35, 1–7.

    Article  Google Scholar 

  7. Kim, Y., Zhang, Y., & Li, P. (2014). Energy efficient approximate arithmetic for error resilient neuromorphic computing. IEEE Transactions on Very Large Scale Integration VLSI Systems, 23(11), 2733–2737.

    Article  Google Scholar 

  8. Zhou, Y., Lin, J., Wang, J., & Wang, Z. (2018, October). Approximate comparator: Design and analysis. In: 2018 IEEE International Workshop on Signal Processing Systems (SiPS) (pp. 1–5). IEEE.

  9. Monajati, M., Fakhraie, S. M., & Kabir, E. (2015). Approximate arithmetic for low-power image median filtering. Circuits, Systems, and SignalProcessing, 34(10), 3191–3219.

    Article  Google Scholar 

  10. Pishvaie, A., Jaberipur, G., & Jahanian, A. (2012). Improved CMOS (4; 2)compressor designs for parallel multipliers. Computers & Electrical Engineering, 38(6), 1703–1716.

    Article  Google Scholar 

  11. Chang, C. H., Gu, J., & Zhang, M. (2004). Ultra low-voltage low-power CMOS 4–2 and 5–2 compressorsfor fast arithmetic circuits. IEEE Transactions on Circuits and Systems I: Regular Papers, 51(10), 1985–1997.

    Article  Google Scholar 

  12. Gorantla, A. (2017). Design of approximate compressors for multiplication. ACM Journal on EmergingTechnologies in Computing Systems (JETC), 13(3), 1–17.

    Article  Google Scholar 

  13. Moaiyeri, M. H., Sabetzadeh, F., & Angizi, S. (2018). An efficient majority-based compressor for approximate computing in the nano era. Microsystem Technologies, 24(3), 1589–1601.

    Article  Google Scholar 

  14. Taheri, M., Arasteh, A., Mohammadyan, S., Panahi, A., & Navi, K. (2020). A novel majority based imprecise 4:2 compressor with respect to the current and future VLSI industry. Microprocessors and Microsystems, 73, 102962.

    Article  Google Scholar 

  15. Asif, S., & Kong, Y. (2014). Low-area wallace multiplier. Vlsi Design. https://doi.org/10.1155/2014/343960

    Article  Google Scholar 

  16. Townsend, W. J., Swartzlander Jr, E. E., & Abraham, J.A. (2003, December). A comparison of Dadda and Wallace multiplier delays. In: Advanced signal processing algorithms, architectures, and implementations XIII (Vol. 5205, pp. 552–560). International Society for Optics and Photonics.

  17. Jaiswal, K. B., Kumar, N., Seshadri, P. & Lakshminarayanan, G. (2015, March). Low power wallace tree multiplier using modified full adder. In 2015 3rd international conference on signal processing, communication and networking (ICSCN) (pp. 1–4). IEEE.

  18. Marimuthu, R., Rezinold, Y. E., & Mallick, P. S. (2016). Design and analysis of multiplier using approximate 15–4 compressor. IEEE Access, 5, 1027–1036.

    Article  Google Scholar 

  19. Bala, S. T., Shangavi, D. & Sangeetha, P. (2018, December). Area and Power Efficient Approximate Wallace Tree Multiplier using 4: 2 Compressors. In 2018 International Conference on Intelligent Computing and Communication for Smart World (I2C2SW) (pp. 287–290). IEEE.

  20. Reda, S., & Shafique, M. (2019). Approximate circuits. Springer.

    Book  Google Scholar 

  21. Shah, T., & Jamal, S. S. (2020). An improved chaotic cryptosystem for image encryption and digital watermarking. Wireless Personal Communications, 110(3), 1429–1442.

    Article  Google Scholar 

  22. Walker, J. S. (2008). A primer on wavelets and their scientific applications. CRC Press.

    Book  MATH  Google Scholar 

  23. Sun, C., Talbot, H., Ourselin, S. & Adriaansen, T. eds. (2003). Digital image computing: techniques and applications. Proceedings of the VIIth Biennial Australian Pattern Recognition Society Conference, DICTA 2003. CSIRO PUBLISHING.

  24. Abraham, A., Jiang, X. H., Snášel, V. & Pan, J. S. eds., (2015). Intelligent data analysis and applications. Proceedings of the Second Euro-China Conference on Intelligent Data Analysis and Applications, ECC 2015 (Vol. 370). Springer.

  25. Maragos, P., Schafer, R. W., & Butt, M. A. (Eds.). (2012). Mathematical morphology and its applications to image and signal processing. Springer.

    Google Scholar 

  26. Seppänen, T. (Ed.). (2008). Digital audio watermarking techniques and technologies: applications and benchmarks. Information Science Reference.

    Google Scholar 

  27. Guo, Y., Sun, H., Guo, L. & Kimura, S. (2018, October). Low-cost approximate multiplier design using probability-driven inexact compressors. In 2018 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS) (pp. 291–294). IEEE.

  28. Tung, C.W. & Huang, S. H. (2019, April). Low-power high-accuracy approximate multiplier using approximate high-order compressors. In 2019 2nd International Conference on Communication Engineering and Technology (ICCET) (pp. 163–167). IEEE.

  29. Marimuthu, R., Bansal, D., Balamurugan, S., & Mallick, P. S. (2013). Design of 8–4 and 9–4 compressors for high speed multiplication. American Journal of Applied Sciences, 10(8), 893.

    Article  Google Scholar 

  30. Silveira, B., Paim, G., Abreu, B., Grellert, M., Diniz, C. M., da Costa, E. A. C., & Bampi, S. (2017). Power-efficient sum of absolute differences hardware architecture using adder compressors for integer motion estimation design. IEEE Transactions on Circuits and Systems I: Regular Papers, 64(12), 3126–3137.

    Article  Google Scholar 

  31. Rouholamini, M., Kavehie, O., Mirbaha, A. P., Jasbi, S. J. & Navi, K. (2007, May). A new design for 7: 2 compressors. In 2007 IEEE/ACS International Conference on Computer Systems and Applications (pp. 474–478). IEEE.

  32. Schiavon, T., Paim, G., Fonseca, M., Costa, E. & Almeida, S., (2016). Exploiting adder compressors for power-efficient 2-D approximate DCT realization. In 2016 IEEE 7th Latin American Symposium on Circuits & Systems (LASCAS) (pp. 383–386). IEEE.

  33. Venkatachalam, S., & Ko, S. B. (2017). Design of power and area efficient approximate multipliers. IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 25(5), 1782–1786.

    Article  Google Scholar 

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Electronics and Communication Engineering, SRM Institute of Science and Technology, Chennai, Tamil Nadu, 603203, India

    M. Maria Dominic Savio & T. Deepa

Authors
  1. M. Maria Dominic Savio
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. T. Deepa
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

MMDS has involved for optimization of proposed work, simulation results analysis, and writing manuscript. TD did the technical revisions of English corrections and grammatical errors.

Corresponding author

Correspondence to M. Maria Dominic Savio.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Savio, M.M.D., Deepa, T. Design of Energy Efficient Multiplier with Approximate Computing on Scalable Compressor for Error-Resilient Image Contrast Enhancement. Wireless Pers Commun 127, 2997–3013 (2022). https://doi.org/10.1007/s11277-022-09907-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-022-09907-4

Keywords