Deep Learning Assisted Transceiver Design Methods for Multisource and Multidestination AF Relay Systems

Abstract

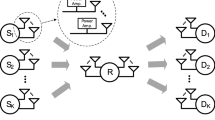
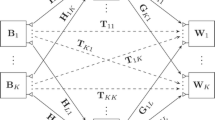
This article studies transceiver design methods for multiple-source and multiple-destination communication systems via an amplify-and-forward relay. Specifically, sum mean-square-error (MSE) minimizing source power allocation schemes, a relay beamforming matrix, and destination filter design methods are developed. After formulating the tractable sum-MSE minimization problem by introducing an auxiliary variable, a block-coordinate-descent-based algorithm is proposed to alternately optimize each transceiver coefficients of source, relay, and destination nodes. Subsequently, deep learning (DL)-assisted design methods are proposed to address the drawbacks of iterative algorithms. Exploiting the structure of the optimum relay beamformer, the proposed DL-based methods return only a single parameter to construct the relay beamforming matrix as well as the transceiver coefficients for the source and destination nodes, thereby, efficiently implementing the deep neural network of the proposed scheme. The effectiveness of the proposed methods was verified through numerical simulations. In particular, without iterative calculations, the DL-based schemes show almost identical performance to that of the optimum methods.

Appendices

Appendix 1: Derivation of Optimal Relay Filter ${{\textbf {F}}}$

For the given source and destination filters, the optimization problem (10) to derive ${\textbf {F}}$ is constrained only by (10.2) Thus, the Lagrangian function can be written as follows:

$$ \begin{aligned} {\mathcal{L}}({\mathbf{F}},\lambda _{r} ) = & \sum\limits_{{i = 1}}^{K} \{ {\mathbf{g}}_{i}^{*} d_{i}^{*} d_{i} {\mathbf{g}}_{i}^{T} {\mathbf{Fh}}_{i} \tilde{p}_{i} {\mathbf{h}}_{i}^{H} {\mathbf{F}}^{H} - \sqrt {\tilde{p}} _{i} {\mathbf{h}}_{i} d_{i} {\mathbf{g}}_{i}^{T} {\mathbf{F}} \\ & \;\;\;\; - \sqrt {\tilde{p}} _{i} {\mathbf{g}}_{i}^{*} d_{i}^{*} {\mathbf{h}}_{i}^{H} {\mathbf{F}}^{H} + {\mathbf{I}}_{{N_{r} }} \;\;\sigma _{{n_{r} }}^{2} \alpha _{s}^{{ - 2}} {\mathbf{g}}_{i}^{*} d_{i}^{*} d_{i} {\mathbf{g}}_{i}^{T} {\mathbf{FF}}^{H} \\ & \;\;\;\; + \sigma _{{n_{i} }}^{2} \alpha _{s}^{{ - 2}} d_{i}^{*} d_{i} {\mathbf{I}}_{{N_{r} }} + \sum\limits_{{k \ne i}}^{K} {{\mathbf{g}}_{k}^{*} } d_{k}^{*} d_{k} {\mathbf{g}}_{k}^{T} {\mathbf{Fh}}_{i} \tilde{p}_{i} {\mathbf{h}}_{i}^{H} {\mathbf{F}}^{H} \} \quad \\ & \;\;\;\; + \lambda _{r} ({\text{Tr}}({\mathbf{F}}(\sum\limits_{{i = 1}}^{H} {{\mathbf{h}}_{i} } \tilde{p}_{i} {\mathbf{h}}_{i}^{H} + \sigma _{{n_{r} }}^{2} {\mathbf{I}}_{{N_{r} }} ){\mathbf{F}}^{H} ) - P_{r} ), \\ \end{aligned} $$

(A.1)

where $\lambda _r$ is the Lagrange multiplier for the relay-node power constraint (10.2). With the Karush (Kuhn) condition [22] and denoting $\alpha _s^2 \lambda _r = {\overline{\lambda }_r}$, the optimum relay filter is obtained by

$$\begin{aligned} {{\textbf {F}}} = \alpha _s \Big ( \sum _{k=1} {{\textbf {g}}}_{k}^{*} d_k^* d_k {{\textbf {g}}}_{k}^{T} + \overline{\lambda }_r {{\textbf {I}}}_{N_r}\Big )^{-1} \Big ( \sum _{j=1}^K {\sqrt{p_j}} {{\textbf {g}}}_{j}^{*} d_j^* {{\textbf {h}}}_j^H \Big ) \Big ( \sum _{i=1}^K {{\textbf {h}}}_i p_i {{\textbf {h}}}_i^H + \sigma _{n_r}^2 {{\textbf {I}}}_{N_r} \Big )^{-1} \end{aligned}$$

(A.2)

Appendix 2: Derivation of optimal source node power allocation scheme

The Lagrangian function of the problem (14) is represented by

$$\begin{aligned}&\mathcal {L}({\tilde{p}}_k, \alpha _s, \lambda _{s,k}, \lambda _{r}^{(s)}) \nonumber \\&= d_k {{\textbf {g}}}_k^T {{\textbf {F}}} {{\textbf {h}}}_k {\tilde{p}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H {{\textbf {g}}}_k^* d_k^* - d_k {{\textbf {g}}}_k^T {{\textbf {F}}} {{\textbf {h}}}_k {\sqrt{\tilde{p}}_k} - {\sqrt{\tilde{p}}_k}{{\textbf {h}}}_k^H {{\textbf {F}}}^H {{\textbf {g}}}_k^* d_k^* + 1 \nonumber \\&\;\;\; + \alpha _s^{-2} \sigma _{n_r}^2 d_k {{\textbf {g}}}_k^T {{\textbf {F}}} {{\textbf {F}}}^H {{\textbf {g}}}_k^* d_k^* + \alpha _s^{-2} \sigma _{n_k}^2 d_k d_k^* + \sum _{i\ne k}^{K} d_i {{\textbf {g}}}_i^T {{\textbf {F}}} {{\textbf {h}}}_k {\tilde{p}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H {{\textbf {g}}}_i^* d_i^* \nonumber \\&\;\;\; + \lambda _{s,k}(\alpha _s^2{\tilde{p}}_k - P_{max} ) + \lambda _{r}^{(s)}(\alpha _s^2 \text {Tr}({{\textbf {F}}} {{\textbf {h}}}_k {\tilde{p}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H)) \end{aligned}$$

(B.1)

The KKT conditions for problem (14) are expressed as follows:

• (i) Stationarity: $\frac{\partial \mathcal {L}}{\partial {\tilde{p}}_k }= 0$ and $\frac{\partial \mathcal {L}}{\partial \alpha _s }= 0$

• (ii) Primal Feasibility:(1) $\alpha _s^2 {\tilde{p}}_k - P_{max} \le 0$ and (2) $\alpha _s^2 \text {Tr}({{\textbf {F}}} {{\textbf {h}}}_k {\tilde{p}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H) - P_{r,k} \le 0$

• (iii) Dual Feasibility: $\lambda _{s,k}\ge 0$ and $\lambda _{r}^{(s)}\ge 0$. Accordingly, it can be obtained that ${\overline{\lambda }}_{s,k} = \alpha _s^2\lambda _{s,k} \ge 0$ and ${\overline{\lambda }}_{r}^{(s)} = \alpha _s^2 \lambda _{r}^{(s)}\ge 0$

• (iv) Complementary Slackness Condition (CSC): (1) ${\overline{\lambda }}_{s,k} (\alpha _s^2 {\tilde{p}}_k - P_{max} )=0$ and (2) ${\overline{\lambda }}_{r}^{(s)}( \alpha _s^2 \text {Tr}({{\textbf {F}}} {{\textbf {h}}}_k {\tilde{p}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H) - P_{r,k} )=0$

With the stationary condition $\frac{\partial \mathcal {L}}{\partial {\tilde{p}}_k }= 0$, the power allocation of $\textsf {S}_k$ can be written as

$$\begin{aligned} {\tilde{p}}_{k}({\overline{\lambda }_{s,k}},{\overline{\lambda }}_{r}^{(s)}) = \Big ( \frac{ \text {Re}(d_k {{\textbf {g}}}^T {{\textbf {F}}} {{\textbf {h}}}_k ) }{ \sum _{i}^{K} d_i {{\textbf {g}}}_i^T {{\textbf {F}}} {{\textbf {h}}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H {{\textbf {g}}}_i^* d_i^* + {\overline{\lambda }_{s,k}} + {\overline{\lambda }}_{r}^{(s)} \text {Tr}({{\textbf {F}}}{{\textbf {h}}}_k {{\textbf {h}}}_k^H {{\textbf {F}}}^H )} \Big )^2 \end{aligned}$$

(B.2)

From $\frac{\partial \mathcal {L}}{\partial \alpha _s }= 0$ in (i) and (iv), we obtain $\phi _k = \overline{\lambda }_{s,k} P_{max} + {\overline{\lambda }}_{r}^{(s)} P_{r,k}$; thus, $\frac{\phi _k - \overline{\lambda }_{s,k} P_{max}}{P_{r,k}}$ can be replaced by ${\overline{\lambda }}_{r}^{(s)}$. In addition, from the primal and dual feasibilities, ${\overline{\lambda }}_{s,k}$ and ${\overline{\lambda }}_{r}^{(s)}$ are bounded by $0 \le {\overline{\lambda }}_{s,k} \le \frac{\phi _k}{P_{max}}$ and $0 \le {\overline{\lambda }}_{r}^{(s)} \le \frac{\phi _k}{P_{r,k}}$, respectively. Based on the bounds of ${\overline{\lambda }}_{s,k}$ and ${\overline{\lambda }}_{r}^{(s)}$, the power allocation of (B.2) can be classified as follows:

• (i) ${\overline{\lambda }}_{s,k}=0$: (B.2) is obtained by $\tilde{p}_k({\overline{\lambda }_{s,k}}=0,{\overline{\lambda }}_{r}^{(s)}=\frac{\phi _k}{P_{r,k}})$ and $\alpha _s$ is determined by the CSC (2) and satisfying the Primal Feasibility (1) with a strict inequality.

• (ii) ${\overline{\lambda }}_{s,k}=\frac{\phi _k}{P_{max}}$: (B.2) is decided by $\tilde{p}_k({\overline{\lambda }_{s,k}}=\frac{\phi _k}{P_{max}},{\overline{\lambda }}_{r}^{(s)}=0)$ and $\alpha _s$ is determined by the CSC (1) and satisfying the Primal Feasibility (2) with a strict inequality.

• (iii) $0<{\overline{\lambda }}_{s,k}<\frac{\phi _k}{P_{max}}$: (B.2) is represented by function of ${\overline{\lambda }_{s,k}}$, i.e.,${\tilde{p}}_{k}({\overline{\lambda }_{s,k}},{\overline{\lambda }}_{r}^{(s)}= \frac{\phi _k - \overline{\lambda }_{s,k} P_{max}}{P_{r,k}})$ and ${\overline{\lambda }_{s,k}}$ is chosen to satisfy both CSC (1) and (2) using the bisection method. In addition, the value of $\alpha _s$ is determined by either CSC (1) or CSC (2).