1 Introduction

1.1 Background and Related Works

In the recent past, wireless communication networks have been employing orthogonal multiple access (OMA) scenarios, in which the communication resources are assigned orthogonally to different users. However, serving OMA users is restricted by the number of orthogonal communication resources, whereas the radio resources are becoming more limited day by day [1]. Besides, the future wireless networks require high speed of data rate with low latency [2]. To meet these challenges, NOMA schemes are being recommended as a promising technique realizing efficient resource utilization and high data rate. Unlike OMA, NOMA employs the same time–frequency resources by allocating various power levels in power-domain (PD) NOMA and assigning various signature codes in code-domain NOMA to different users. However, NOMA comes with increasing the intra-cell interferences, which can be reduced by implementing the successive interference cancellation (SIC) algorithm at each user. In addition to the ability of serving different users in an identical resource block (RB), which is useful to meet the increasing demand for massive communications, NOMA can improve both spectral efficiency and user fairness which are appropriate reasons for employing NOMA in 5G and beyond networks [3].

Furthermore, the cooperative relaying has been efficiently combined with the NOMA scheme to achieve better performance [4, 5]. In these scenarios, the users with stronger channel gains act as relays for the users with weaker channel gains. A cooperative NOMA scheme has been proposed to enhance the outage probability of the system in [6]. Also, in [7], the outage probability and ergodic rate performance in a downlink cooperative NOMA scenario were studied, where the base station transmits the users’ information simultaneously using a half-duplex (HD) relay. The mutual information and outage probability analysis of an uplink NOMA in a two-hop cooperative cellular scenario with frequency selective fading channels were studied in [8]. In [9], the secrecy performance of a NOMA-based scheme in conjunction with a full-duplex (FD) two-way relay was investigated.

On the other hand, interference is always a challenging issue in cellular networks. Inter-cell interference from the adjacent BSs and intra-cell interference in NOMA-based communication can limit the system performance. In [1], the principles of uplink and downlink NOMA communication were presented. In addition, their main distinctions in the presence of intra-cell and inter-cell interference (ICI) were investigated. The outage probability of NOMA, considering the effects of both intra-cell and inter-cell interferences, as well as imperfect channel state information (CSI) and SIC has been studied in [2]. In [10], it has been shown that the interference in a multi-cell downlink transmission can be reduced using NOMA in the Massive Multiple-Input Multiple-Output (mMIMO) system compared to a standalone mMIMO system. In [11], the effect of practical imperfect SIC on the bit error rate (BER) in a cellular downlink NOMA scheme was investigated. Some available researches on resource allocation and inter-cell interference reduction in multi-cell NOMA schemes were briefly reviewed in [12], where a novel signal model was developed for downlink coordinated multi-point (CoMP) NOMA. In [13], the distributed power allocation problem for a multi-cell uplink NOMA system was studied, where the inter-cell interference was treated as additive Gaussian noise. Also, a multi-cell MIMO–NOMA network and two coordinated beamforming (CBF) methods based on downlink interference alignments were presented in [14], in which the beamforming vectors of two base stations (BS) are optimized in order to cancel inter-cell interference and improve the rate performance of cell-edge users. In [15], a multi-cell network was suggested using the CoMP NOMA scheme. Also, the outage performance of the users was theoretically analyzed. The coverage probability and rate of users in a downlink NOMA with symbiosis of aerial and terrestrial users have been studied in [16]. Moreover, a NOMA-based scheme in a downlink Poisson multi-cell network has been proposed in [17], where the author’s purpose is to optimize the cell sum rate in the presence of inter-cell interference. A general multi-cell NOMA network for achieving optimal user clustering and power assignment considering inter-cell interference has been presented in [18]. The outage probability of a multi-cell NOMA scenario in the presence of interference has been analyzed in [19]. In addition, a two-cell downlink NOMA system with co-channel interference has been considered in [20].

Furthermore, there are numerous relay selection criteria that are widely used in the NOMA-based works. A two-hop cooperative scheme based on NOMA was proposed in [21], where a DF relay with the best channel quality towards the far-user is chosen to retransmit the far-user’s signal and this cooperation also facilitates the interference cancellation of the near-user. In [22], the author aims to investigate the effect of correlated fading channels on the outage performance for a NOMA system with DF relaying, where a three-stage relay selection model has been deployed to improve the performance. The secrecy outage of a cooperative NOMA network in the presence of multiple potential relays and an eavesdropper has been analyzed in [23] employing a two-stage single relay selection algorithm to enhance the secrecy performance. NOMA with Amply-and-Forward (AF) partial relay selection for the far user and direct transmission for the near user has been combined in [24] to improve the outage performance. Adaptive relay selection following power assignment in a two-phase cooperative underlay cognitive radio NOMA network has been presented in [25]. Also, the outage probability of a NOMA scenario with a two-stage relay selection strategy has been studied in [26]. The outage performances of two relay selection schemes in a FD-NOMA network have been derived in [27]. In [28], a two-phase cooperative NOMA network over Nakagami-m fading channels has been presented, where the relay selection scheme intends to optimize the system sum rate. A downlink cooperative NOMA network with two users and multiple relays has been introduced in [29], where two optimal two-stage relay selection algorithms with fixed and adaptive power allocation have been proposed. The secrecy outage probability of a downlink NOMA system that jointly implements relay and antenna selection has been investigated in [30]. In [31], the secure outage probability and ergodic secrecy capacity of a NOMA-FD relaying system has been investigated, where the best relay is selected among multiple FD relays. A joint buffer-aided multi-relay cooperative NOMA scheme with partial relay selection has been developed in [32]. The outage probability of a downlink NOMA system under best relay selection and imperfect successive interference cancellation has been studied in [33]. In [34], A NOMA scheme closed form expression of outage probability considering an imperfect CSI has been derived in order to evaluate the performance of partial relay selection scheme. The outage performance analysis of some relay selection schemes in underlay cognitive NOMA networks has been studied in [35].

1.2 Motivation and Contributions

To the best of our knowledge, the existing works on the cooperative NOMA considering the inter-cell interference have focused either on the CoMP transmission, where multiple BSs transmit jointly for the same edge users, or on the beamforming method. These methods require the channel conditions of the cell-edge users at all adjacent BSs. Moreover, some works simply treat the inter-cell interference as additive Gaussian noise. However, our proposed method considers a more realistic scenario, where the main cell nodes are not aware of the adjacent BSs channel conditions and their transmissions are considered as inter-cell interference, which may limit the performance of the main cell users. We have potential relays between the BS and the cell-edge users, where they receive the users’ information based on NOMA and their performances are defected by inter-cell interference. This inter-cell interference causes that the SINR constraints for guaranteeing the SIC performance are not satisfied for NOMA nodes, unlike the previous works. On the other hand, the fairness condition in a NOMA scheme is also considered. Hence, we have the new constraints to be considered jointly in the optimization problems which make the problems more general. In other words, we present a more general scenario that consider both fairness and SIC guaranteeing performance constraints which are not jointly considered in the existing literature, to the best of our knowledge. For dealing with the intra-cell interference effects, we suggest a novel relay selection which unlike the existing works, selects one relay per user in the main cell. In fact, in the existing works employing the cooperative NOMA strategy, just one relay (best relay) is selected for helping the BS to improve the system reliability. When one relay is employed, the probability that the channel gains from that relay to both users be suitable is low. Moreover, we can just select the relays that are able to detect the signal of both users. Therefore, even if we obtain the required performance, it is so likely that we will not achieve the best possible performance. Hence, we employ one relay per user in the proposed scheme. This offer increases the degrees of freedom in our scheme and improves the performance, where the best relay with the best condition can be selected for each user. Moreover, the proposed criterion not only tries to select the best relay for each edge-user, but also considers the interference effects from the selected relays on the non-corresponding users. Hence, an efficient relay selection criterion is proposed to jointly improve the performance of each cell-edge user and mitigate the intra-cell interference impression by considering the interference channels in the relay selection criterion. In fact, we propose a novel relay selection, so that despite having the best conditions for the corresponding user, it has the least interference effect on the other user which can improve the system performance in terms of rate. It should be noted that we analyzed the performance of the proposed scheme considering the effect of inter-cell interference, which is more realistic. Moreover, we compute and present the relay selection computational complexities of the proposed scheme, the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25].

Here, we have non-convex optimization problems which force us to propose the problem transformation and iterative algorithms for solving them. It should be noted that this scenario can be extended to a model with multiple selected relays and multiple cell-edge users by employing a new pairing strategy between cell-center relays and cell-edge users, which can better represent the superiority of our proposed method and can be considered as an attractive scenario for the future work.

In this paper, we present a cooperative power domain NOMA for a downlink multi-cell network consisting of a BS, multiple potential relays, and two cell-edge users in the main cell. No direct link between the BS and the users is assumed. The BS sends the information of users to the relays based on the NOMA strategy, and two selected relay nodes adopting the DF decoding act as HD relays for the cell-edge users. In addition, there are two adjacent interfering cells. The main contributions of this paper are shorted as follows:

  • cooperative NOMA scenario is investigated for improving the sum rate and energy efficiency. To the best of our knowledge, one relay assignment per cell-edge user in a multi-cell cooperative NOMA network is suggested for the first time. The selected relays detect the corresponding cell-edge user data and retransmit the detected data in the second phase. Therefore, the sum rate formulation and theoretical analysis of this system model are different and more complex than the previous researches and have not been studied yet.

  • Due to the inter-cell interference, the NOMA SINR constraints for guaranteeing the SIC performance are not satisfied at the selected relay nodes. Also, the fairness condition is considered in the proposed scheme. Hence, more general optimization problems with the new constraints are introduced.

  • There will be a two relay-user pairing, which aims to improve the performance and mitigate the interference impression and may cause more novelty.

  • A novel relay selection criterion is proposed based on both the channel conditions between the potential relays and the corresponding users and the channel coefficient between the relays and the non-corresponding users.

  • Due to the non-convexity of the optimization problems, a suboptimal approach is suggested to obtain the power allocation for the sum rate and energy efficiency maximization by iteratively solving the non-convex problems. We use the transformation and bisection algorithm for solving the sum rate maximization problem while an efficient combination of transformation, three-stage bisection method, and Dinkelbach algorithm is employed to efficiently solve the energy efficiency optimization problem.

  • The proposed method is compared with the Max–Min criterion, two new relay selection schemes in [21] and [25], and exhaustive search relay selection scheme. The results depict the superior performance of the proposed method over the Max–Min scheme and the relay selection strategies in [21] and [25] in the sense of both the sum rate and energy efficiency while its performance is so close to the exhaustive search relay selection method with less complexity.

The relay selection computational complexities of the proposed scheme, the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] are provided in this paper. The results show that the complexity order of the proposed scheme is linear in the number of potential relays.

1.3 Organization

The remainder of the paper is structured as follows. The system model and problem formulations are derived in Sect. 2. Then, Sect. 3 develops the optimization problems and suboptimal power allocation algorithms for maximizing the system’s sum rate and energy efficiency, respectively. Section 4 presents the computational complexity of the proposed scheme and some existing literature. The performance of the proposed algorithms is evaluated by simulations in Sect. 5, and finally the conclusion is presented.

Notations: Through the paper, \({\mathbb{E}}\left\{.\right\}\) is the expectation operator, \(\left|x\right|\) denotes the absolute value of variable \(x\), \({\text{log}}(.)\) indicates the logarithm operator, and \(\mathcal{O}\left(.\right)\) stands for complexity order.

2 System Model and Problem Formulation

In this section, the network description and signal model are illustrated. In addition, the criterion for the relay selection scheme is presented.

2.1 Network Description

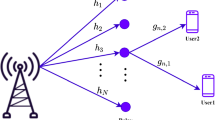
Consider a NOMA downlink cooperative network with three cells. There is a main cell consisting of one BS and two users in addition to multiple potential relays distributed in the cell, while there are two interfering cells. Our focus is more on the main cell. Let the set of indices of the relays in the main cell be \(\mathcal{R}=\left\{\mathrm{1,2},\dots ,K\right\}\). Two potential relays must be selected for the cell-edge users, one relay for each user. The maximum power available at the relays is considered to be less than the BS. Also, the effect of inter-cell interference from two neighbor cells is only considered on the potential relays, and the cell-edge users of the main cell are not affected by the inter-cell interference due to the long distance and shadowing. Both the relays and users are equipped with a single transmit antenna, and the BS also has a single antenna [36]. The BS is not able to transmit directly to the users and the relays operate in HD mode.

The system model is shown in Fig. 1. In our system model, the BS sends the superposition of all users’ signals based on PD-NOMA in the first phase. In the second phase, the selected relays retransmit only the corresponding cell-edge users’ signals to improve the system’s performance. It should be noted that among the potential relays, the one that has a maximum channel gain ratio of the one cell-edge user to the other cell-edge user is selected as the relay for that user.

Fig. 1
figure 1

System model

Full size image

Let \({h}_{s{r}_{i}}\) denote the channel coefficient between the BS and potential relay \(\left(i=1,\dots ,K\right)\). Also, \({h}_{{r}_{i}{d}_{j}}| j\epsilon \left\{\mathrm{1,2}\right\}\) denotes the channel coefficient between the potential relay \(i\) and the cell-edge user \(j\). The channel gains can be viewed as exponentially distributed random variables, provided that the channels are fading with Rayleigh distribution. We assume that the perfect CSI is obtained with negligible overhead before each signalling interval.

2.2 Signal Model and Relay Selection Scheme

In the proposed model, the superimposed signal transmitted by the main BS can be expressed as:

$$ S\left( t \right) = \mathop \sum \limits_{i = 1}^{2} \sqrt {P_{s} \alpha_{i} } x_{{r_{i} }} \left( t \right) $$
(1)

where \({P}_{s}\) denotes the available power of the main cell BS and \({\mathrm{\alpha }}_{{\text{i}}}\) is the power assignment coefficient for the \(i\)-th selected relay. Also, \({x}_{{r}_{i}}\) represents the signal of the \(i\)-th selected relay. Without loss of generality, we assume that \(\left|{h}_{s{r}_{1}^{*}}\right|\ge \left|{h}_{s{r}_{2}^{*}}\right|\) (\({h}_{s{r}_{i}^{*}}\) indicates the channel coefficient between the \(i\)-th selected relay and main cell BS) leading to power allocation coefficients in the descending order as\({\alpha }_{2}\ge {\alpha }_{1}\). Moreover, the transmitted signal for relays should be such that\({\mathbb{E}}\left\{{\left|{x}_{{r}_{i}}\right|}^{2}\right\}=1 ,i\epsilon \left\{\mathrm{1,2}\right\}\). The criteria for selecting the relays can now be expressed as follows:

$$ r_{1}^{*} = max\left\{ {min\left( {\left| {h_{{sr_{i} }} } \right|^{2} ,\left| {h_{{r_{i} d_{1} }} } \right|^{2} /h_{{r_{i} d_{2} }} } \right)} \right\}, \quad i = 1, \ldots ,K $$
(2)
$$ r_{2}^{*} = max\left\{ {min\left( {\left| {h_{{sr_{i} }} } \right|^{2} ,\left| {h_{{r_{i} d_{2} }} } \right|^{2} /h_{{r_{i} d_{1} }} } \right)} \right\}, \quad i = 1, \ldots ,K $$
(3)

The signal received at the \(i\)-th selected relay can be represented as follows:

$$ y_{{r_{i}^{*} }} \left( t \right) = h_{{sr_{i}^{*} }} S\left( t \right) + \mathop \sum \limits_{k = 1}^{2} \sqrt {P_{{B_{k} }} } h_{{B_{k} r_{i}^{*} }} + n_{{r_{i}^{*} }} \left( t \right) , i = 1,2 $$
(4)

where \({n}_{{r}_{i}^{*}}\left(t\right)\) denotes additive white Gaussian noise (AWGN) at the \(i\)-th selected relay with complex Gaussian distribution of zero mean and covariance of \({N}_{0}\). The AWGN is assumed to be independent and identically distributed (i.i.d.) at all nodes. Furthermore, \({h}_{{B}_{k}{r}_{i}^{*}}\) is the channel coefficient between the \(i\)-th selected relay and the \(k\)-th adjacent cell BS and \({S}_{{B}_{k}}(t)\) denotes the signal transmitted by the \(k\)-th interfering cell. The received signal at the \(i\)-th user can be expressed as:

$$ y_{{d_{i} }} \left( t \right) = h_{{r_{1}^{*} d_{i} }} S_{1} \left( t \right) + h_{{r_{2}^{*} d_{i} }} S_{2} \left( t \right) + n_{{d_{i} }} \left( t \right), i = 1,2 $$
(5)

where \({n}_{{d}_{i}}\left(t\right)\) denotes the additive white Gaussian noise at the \(i\)-th user with complex Gaussian distribution of zero mean and covariance of \({N}_{0}\), \({S}_{1}\left(t\right)\) is the signal transmitted by the first selected relay and \({S}_{2}\left(t\right)\) is the signal transmitted by the second selected relay.

In this paper, we present the sum-rate and energy efficiency optimization problems subject to the maximum available power at the transmission nodes, the NOMA SINR constraints, and also the constraints on the minimum target rate values. First, the achievable rate formulas in two transmission phases are introduced. The achievable rate at the first selected relay in the BS transmission phase after applying the NOMA-based SIC and assuming \(\left|{h}_{s{r}_{1}^{*}}\right|\ge \left|{h}_{s{r}_{2}^{*}}\right|\) is expressed as:

$$ R_{1}^{{T_{1} }} = \frac{1}{2}\log \left( {1 + \frac{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{Int_{1} + N_{0} }}} \right) $$
(6)

where \({p}_{{s}_{1}}={P}_{s}{\alpha }_{1}\) is the power assigned to the selected relay with the better channel condition and \({Int}_{1}=\sum_{k=1}^{2}\sqrt{{P}_{{B}_{k}}}{\left|{h}_{{B}_{k}{r}_{1}^{*}}\right|}^{2}\), where \({P}_{{B}_{k}}\) denotes the transmit power at the \(k\)-th interfering cell. Now, the achievable rate at the second selected relay in the BS transmission phase can be given by:

$$ R_{2}^{{T_{1} }} = \frac{1}{2}\log \left( {1 + \frac{{p_{{s_{2} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} + Int_{2} + N_{0} }}} \right) $$
(7)

where \({p}_{{s}_{2}}={P}_{s}{\alpha }_{2}\) is the power assigned to the selected relay with the weaker channel condition and \({Int}_{2}=\sum_{k=1}^{2}\sqrt{{P}_{{B}_{k}}}{\left|{h}_{{B}_{k}{r}_{2}^{*}}\right|}^{2}\). The achievable rate for user 1 in the second phase can be represented as follows:

$$ R_{1}^{{T_{2} }} = \frac{1}{2}\log \left( {1 + \frac{{p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{1} }} } \right|^{2} }}{{p_{{r_{2} }} \left| {h_{{r_{2}^{*} d_{1} }} } \right|^{2} + N_{0} }}} \right) $$
(8)

where \({p}_{{r}_{1}}\) and \({p}_{{r}_{2}}\) are the power assigned to user 1 and user 2 at the first and second selected relay, respectively. In addition, \(\left|{h}_{{r}_{1}^{*}{d}_{1}}\right|\) and \(\left|{h}_{{r}_{2}^{*}{d}_{1}}\right|\) denote the channel gain between the first selected relay and user 1 and the channel gain between the second selected relay and user 1, respectively. The achievable rate for the user 2 in the second phase can be given by:

$$ R_{2}^{{T_{2} }} = \frac{1}{2}\log \left( {1 + \frac{{p_{{r_{2} }} \left| {h_{{r_{2}^{*} d_{2} }} } \right|^{2} }}{{p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} + N_{0} }}} \right) $$
(9)

where \(\left|{h}_{{r}_{2}^{*}{d}_{2}}\right|\) and \(\left|{h}_{{r}_{1}^{*}{d}_{2}}\right|\) denote the channel gain between the second selected relay and user 2 and the channel gain between the first selected relay and user 2, respectively. Finally, according to the DF relaying method, the achievable rates for user 1 and user 2 are obtained as (10) and (11), respectively.

$$ R_{1} = min\left( {R_{1}^{{T_{1} }} ,R_{1}^{{T_{2} }} } \right) $$
(10)
$$ R_{2} = min(R_{2}^{{T_{1} }} ,R_{2}^{{T_{2} }} ) $$
(11)

3 Analysis of Optimization Problems

This section provides the analysis of the sum-rate and energy efficiency of the proposed model in two subsections, respectively. In addition, the iterative Algorithms for achieving the maximum performance in perspective of sum-rate and energy efficiency are presented. Moreover, we discuss about the convexity of our optimization problems.

3.1 Sum-rate Maximization Analysis

Based on (10) and (11), the sum-rate formulation can be simply defined as \({R}_{sum}={R}_{1}+{R}_{2}\). Accordingly, the sum-rate optimization problem is expressed as (12). It is worth noting that constraints \(C1\) and \(C2\) indicate that the minimum target data rate should be satisfied. Also, constraints \(C3-C4\) and \(C5\) demonstrate that the transmission power allocated at the selected relays and the BS should be lower than the available transmission powers \({{p}_{{r}_{i}}}^{max}\) and \({{P}_{s}}^{max}\), respectively. Constraints \(C6-C7\) guarantee that the near selected relay can decode the signal of the far selected relay. Constraints \(C8-C11\) imply that all the transmission powers should be non-negative.

$$ \mathop {\max }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} }} R_{1} + R_{2} $$
$$ \begin{gathered} C1:\;R_{1} \ge R_{1}^{min} \to R_{1}^{{T_{1} }} \ge R_{1}^{min} \& R_{1}^{{T_{2} }} \ge R_{1}^{min} \hfill \\ C2: \;R_{2} \ge R_{2}^{min} \to R_{2}^{{T_{1} }} \ge R_{2}^{min} \& R_{2}^{{T_{2} }} \ge R_{2}^{min} \hfill \\ C3-C4: \;p_{{r_{i} }} \le p_{{r_{i} }}^{max} , i = 1,2 \hfill \\ C5:\;\mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} \le P_{s}^{max} \hfill \\ C6: \;\frac{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \ge \frac{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \to p_{{s_{2} }} \ge p_{{s_{1} }} \hfill \\ C7: \;\frac{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \ge \frac{{p_{{s_{2} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} + Int_{2} + N_{0} }} \hfill \\ C8-C9:\;p_{{s_{i} }} \ge 0 ,\quad i = 1,2 \hfill \\ C10-C11: p_{{r_{i} }} \ge 0 , \quad i = 1,2 \hfill \\ \end{gathered} $$
(12)

First, we should discuss about the convexity of the problem in (12). It should be noted that while the objective function in (12) is non-convex due to the logarithmic and fractional rate functions, the constraints \(C1-C2\) and (after applying the exponential function on two sides of the constraints) and also the constraints \(C3-C11\) are linear and therefore convex. Hence, we can’t solve the maximization problem employing the standard optimization solvers and must transform the objective function. To deal with this problem, two variables namely \({r}_{1}=min({R}_{1}^{{T}_{1}},{R}_{1}^{{T}_{2}})\) and \({r}_{2}=min({R}_{2}^{{T}_{1}},{R}_{2}^{{T}_{2}})\) are introduced to replace the functions \({R}_{1}\) and \({R}_{2}\), respectively to have a linear (convex) objective function based on \({r}_{1}\) and \({r}_{2}\) [37]. But, with this conversion the constraints \({R}_{1}^{{T}_{1}}\ge {r}_{1}\), \({R}_{1}^{{T}_{2}}\ge {r}_{1}\), \({R}_{2}^{{T}_{1}}\ge {r}_{2}\), and \({R}_{2}^{{T}_{2}}\ge {r}_{2}\) are added to the optimization problem which should be proved that are all convex (convexity is determined by computing of Hessian matrix eigenvalues (\({\lambda }_{eig}\))). For example, we obtain these eigenvalues for the constraint \({R}_{2}^{{T}_{2}}\ge {r}_{2}\) with parameters \({p}_{{r}_{2}}\), \({p}_{{r}_{1}}\), and \({r}_{2}\) as follows:

$$ \begin{gathered} R_{2}^{{T_{2} }} \ge r_{2} \Rightarrow \frac{1}{2}\log \left( {1 + \frac{{p_{{r_{2} }} \left| {h_{{r_{2}^{*} d_{2} }} } \right|^{2} }}{{p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} + N_{0} }}} \right) \ge r_{2} \to \hfill \\ p_{{r_{2} }} \left| {h_{{r_{2}^{*} d_{2} }} } \right|^{2} \ge \left( {p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} + N_{0} } \right)\left( {2^{{2r_{2} }} - 1} \right) \hfill \\ H = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & {2\left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} 2^{{2r_{2} }} } \\ 0 & {2\left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} 2^{{2r_{2} }} } & {4\left( {p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} + N_{0} } \right)\left( {2^{{2r_{2} }} } \right)} \\ \end{array} } \right] \hfill \\ \left| {\lambda_{eig} I - H} \right| = 0 \to \lambda_{eig}^{2} \left( {\lambda_{eig} - 4\left( {p_{{r_{1} }} \left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} + N_{0} } \right)\left( {2^{{2r_{2} }} } \right)} \right) - \lambda_{eig} \left( {2\left| {h_{{r_{1}^{*} d_{2} }} } \right|^{2} 2^{{2r_{2} }} } \right)^{2} = 0 \hfill \\ \end{gathered} $$
(13)

where \(I\) is the identity matrix. It can be shown that the eigenvalues in (13) include a dominant positive value, a zero value, and a value very close to zero. Hence, the Hessian matrix in (13) is semi-definite resulting the constraint \({R}_{2}^{{T}_{2}}\ge {r}_{2}\) is convex. This result is also hold for the other new introduced constraints defined as \({R}_{1}^{{T}_{2}}\ge {r}_{1}\) and \({R}_{2}^{{T}_{1}}\ge {r}_{2}\). On the other hand, the constraint \({R}_{1}^{{T}_{1}}\ge {r}_{1}\) is linear. In this way, the sum-rate optimization problem becomes a convex problem. It is worth noting that, if we set \({r}_{1}\ge {{R}_{1}}^{min}\) and \({r}_{2}\ge {{R}_{2}}^{min}\), the constraints \(C1\) and \(C2\) on \({{R}_{1}}^{min}\) and \({{R}_{2}}^{min}\) in (12) can be satisfied. Accordingly, the modified and convex sum-rate optimization problem can be presented in (14).

$$ \begin{gathered} \mathop {\max }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} ,r_{1} ,r_{2} }} r_{1} + r_{2} \hfill \\ C1:\;R_{1} \ge r_{1} \to R_{1}^{{T_{1} }} \ge r_{1} \& R_{1}^{{T_{2} }} \ge r_{1} \hfill \\ C2: \;R_{2} \ge r_{2} \to R_{2}^{{T_{1} }} \ge r_{2} \& R_{2}^{{T_{2} }} \ge r_{2} \hfill \\ C3-C11:\;C3- C11\;{\text{in}}\;(12) \hfill \\ C12-C13: r_{i} \ge R_{i}^{min} , \quad i = 1,2 \hfill \\ \end{gathered} $$
(14)

Compared to (12), constraints \(C1\) and \(C2\) have been replaced and constraints \(C12\) and \(C13\) have been added to the optimization problem. Although the problem in (14) is a convex problem, obtaining the parameters of the optimization problem using the standard solvers (Lagrangian method) is accompanied by high complexity, where the Lagrangian equation contains both linear and exponential terms. On the other hand, the ranges of the variables \({r}_{1}\) and \({r}_{2}\) are approximately known leading us to propose an iterative algorithm based on the bisection method to solve the optimization problem [37]. Therefore, knowing the values of \({r}_{1}\) and \({r}_{2}\) in each iteration, we propose a new convex problem with the new objective function and the same constraints for the sum-rate maximization problem as:

$$ \begin{gathered} \mathop {\min }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} }} \mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} + \mathop \sum \limits_{k = 1}^{2} p_{{r_{k} }} \hfill \\ C1-C13\;{\text{in }}(14) \hfill \\ \end{gathered} $$
(15)

It should be said that the constraint \(C7\) in (14) is an important constraint which guarantees the SIC performance at the near node in the NOMA-based strategies. In previous researches, this constraint is usually satisfied by itself in the basic NOMA schemes, where the inter-cell interference effect is not considered, or the authors ignored it for simplicity. In the presence of inter-cell interference, we must consider \(C7\). On the other hand, we present for the first time a more general problem where both constraints \(C6\) and \(C7\) are considered in order to jointly satisfy the fairness condition and guarantee the SIC performance in the NOMA scheme. Hence, we have an optimization problem with a more realistic scenario and more general solution. The iterative sum-rate optimization Algorithm (Algorithm 1) based on the bisection method has been proposed in Table 1. It is worth noting that Algorithm 1 and Algorithm 2 are proposed for solving the sum rate and energy efficiency optimization, respectively.

Table 1 Sum-rate iterative optimization Algorithm
Full size table

3.2 Energy Efficiency Maximization Analysis

This section presents the analysis of the energy efficiency problem, proposing an iterative algorithm is suggested to obtain the optimal resource allocation for maximizing the energy efficiency of the system. It is worth noting that we define energy efficiency as the achievable sum rate over the total power consumption. The total power in our scheme is the sum of the power consumed at the BS, the power consumed at the selected relays, and the circuit power consumption. The energy efficiency optimization problem is derived in (16), where \(P_{c}\) indicates the circuit power consumption. As can be seen from (16), the objective function is a fractional function and is not convex. However, the constraints are similar to the sum-rate maximization problem and hence convex. First, the variables \(r_{1}\) and \(r_{2}\) are introduced into the numerator of the energy efficiency objective function to replace the functions \(R_{1}\) and \(R_{2}\), respectively. This reformulation adds convex constraints \(R_{1}^{{T_{1} }} \ge r_{1}\), \(R_{1}^{{T_{2} }} \ge r_{1}\), \(R_{2}^{{T_{1} }} \ge r_{2}\), and \(R_{2}^{{T_{2} }} \ge r_{2}\) to the optimization problem. Given \(r_{1} \ge R_{1}^{min}\) and \( r_{2} \ge R_{2}^{min}\), the constraints \(R_{1}^{{T_{1} }} \ge R_{1}^{min}\), \(R_{1}^{{T_{2} }} \ge R_{1}^{min}\), \(R_{2}^{{T_{1} }} \ge R_{2}^{min}\), and \(R_{2}^{{T_{2} }} \ge R_{2}^{min}\) are eliminated from the optimization problem, so that the transformed optimization problem can be derived in (17). The optimization problem is still not convex. However, both the numerator and the denominator of the fractional objective function are linear over the parameters of the optimization problem and thus either convex or concave. Therefore, it is possible to use the Dinkelbach method [38] and transform the optimization problem into (18). We should know that \(\eta\) in the (18) is a positive parameter. The optimal solution can be found by solving the problem parameterized by \(\eta\) such that \(F\left( \eta \right) = \left( {r_{1} + r_{2} } \right) - \eta \left( {\mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} + \mathop \sum \limits_{k = 1}^{2} p_{{r_{k} }} + P_{c} } \right) = 0\) [39].

$$ \begin{gathered} \mathop {\max }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} }} \left( {R_{1} + R_{2} } \right)/\left( {\mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} + \mathop \sum \limits_{k = 1}^{2} p_{{r_{k} }} + P_{c} } \right) \hfill \\ C1: \;R_{1} \ge R_{1}^{min} \to R_{1}^{{T_{1} }} \ge R_{1}^{min} \& R_{1}^{{T_{2} }} \ge R_{1}^{min} \hfill \\ C2: \;R_{2} \ge R_{2}^{min} \to R_{2}^{{T_{1} }} \ge R_{2}^{min} \& R_{2}^{{T_{2} }} \ge R_{2}^{min} \hfill \\ C3-C4: p_{{r_{i} }} \le p_{{r_{i} }}^{max} , \quad i = 1,2 \hfill \\ C5:\; \mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} \le P_{s}^{max} \hfill \\ C6:\, \frac{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \ge \frac{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \to p_{{s_{2} }} \ge p_{{s_{1} }} \hfill \\ C7:\;\frac{{p_{{s_{2} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{1}^{*} }} } \right|^{2} + Int_{1} + N_{0} }} \ge \frac{{p_{{s_{2} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} }}{{p_{{s_{1} }} \left| {h_{{sr_{2}^{*} }} } \right|^{2} + Int_{2} + N_{0} }} \hfill \\ C8-C9: \;p_{{s_{i} }} \ge 0 , \quad i = 1,2 \hfill \\ C10-C11: p_{{r_{i} }} \ge 0 , \quad i = 1,2 \hfill \\ \end{gathered} $$
(16)
$$ \begin{gathered} \mathop {\max }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} ,r_{1} ,r_{2} }} \left( {r_{1} + r_{2} } \right)/\left( {\mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} + \mathop \sum \limits_{k = 1}^{2} p_{{r_{k} }} + P_{c} } \right) \hfill \\ C1: \; R_{1} \ge r_{1} \to R_{1}^{{T_{1} }} \ge r_{1} \& R_{1}^{{T_{2} }} \ge r_{1} \hfill \\ C2:\;R_{2} \ge r_{2} \to R_{2}^{{T_{1} }} \ge r_{2} \& R_{2}^{{T_{2} }} \ge r_{2} \hfill \\ C3-C11:\;C3 - C11\;{\text{in }}(16) \hfill \\ C12-C13: r_{i} \ge R_{i}^{min} , \quad i = 1,2 \hfill \\ \end{gathered} $$
(17)
$$ \begin{gathered} \mathop {\max }\limits_{{p_{{s_{1} }} ,p_{{s_{2} }} ,p_{{r_{1} }} ,p_{{r_{2} }} }} \left( {r_{1} + r_{2} } \right) - \eta \left( {\mathop \sum \limits_{k = 1}^{2} p_{{s_{k} }} + \mathop \sum \limits_{k = 1}^{2} p_{{r_{k} }} + P_{c} } \right) \hfill \\ C1-C13\;{\text{in}}\;(17) \hfill \\ \end{gathered} $$
(18)

The energy efficiency optimization problem is now convex. Similar to the sum rate maximization problem, the ranges of the variables \(r_{1}\) and \(r_{2}\) are known and therefore it is possible to propose and employ an iterative algorithm on the basis of the bisection method to solve the optimization problem. This algorithm (Algorithm 2) is shown in Table 2. For the sake of clarity, it should be mentioned that we have presented an iterative algorithm with an inner loop namely the three-stage bisection method, and an outer loop namely the Dinkelbach method.

Table 2 Energy efficiency optimization Algorithm
Full size table

We know that energy efficiency has a Gaussian behaviour with respect to power consumption. On the other hand, the data rate increases logarithmically with power consumption. As a result, it can be found that the energy efficiency function has a Gaussian behaviour over the rate variables. Hence, in the proposed algorithm we achieve the optimal rate of each user based on the three-stage bisection method within the maximization of the energy efficiency function, where in each iteration we employ the three times bisection method instead of employing once as compared to the general bisection method and achieve three rate values in each iteration. When these three values become equal, the convergence is obtained, and the inner loop is completed. It is worth noting that the optimization problems, after being transformed into convex problems, can be solved by the usual convex problem solution. However, by using the proposed algorithms instead of analyzing and solving the problems based on the numerous parameters and equations, we achieve the optimal solution with less complexity.

4 Computational Complexity

This section presents the computational complexity of the proposed relay selection scheme and compares it with the complexity of the existing schemes. For analyzing the complexity of the proposed relay selection scheme, we need to know what steps are taken in this scheme. First, the channel gain ratio from each relay to cell-edge users should be calculated. The complexity of this process for \(K\) potential relays is equal to \(K \approx {\mathcal{O}}\left( K \right)\). In addition, the min operation for potential relays imposes the complexity of \({\mathcal{O}}\left( K \right)\) to the system. In the following, the max operation on the \(K\) obtained values is a process with \({\mathcal{O}}\left( K \right)\) computational complexity. After selecting the first relay and removing it from the list of potential relays, a similar computation for \(K - 1 \approx {\mathcal{O}}\left( K \right)\) remained potential relays should be performed for selecting the second relay. In this way, the total complexity of the proposed relay selection scheme can be presented as:

$$ proposed\;scheme\;complexity = K + {\mathcal{O}}\left( K \right) + {\mathcal{O}}\left( K \right) + K - 1 + {\mathcal{O}}\left( {K - 1} \right) + {\mathcal{O}}\left( {K - 1} \right) \approx {\mathcal{O}}\left( K \right) $$
(19)

It can be seen that the proposed scheme is linear in the number of potential relays. As the same way, the complexity of the max–min scheme for selecting two relays can be expressed as:

$$ max{-}min;scheme\;complexity = {\mathcal{O}}(K) + {\mathcal{O}}(K) + {\mathcal{O}}(K - 1) + {\mathcal{O}}(K - 1) \approx {\mathcal{O}}(K) $$
(20)

This equation proves that the max–min is also linear in the number of potential relays. Of course, our proposed scheme is a bit more complicated than the max–min scheme. This comes from the employing division operator in the proposed scheme.

In the following, we present the complexity order of two recent relay selection schemes which are proposed in the [21] and [25]. In these schemes, relay selections are implemented in two stages. In the first stage of the scheme proposed in [21], the potential relays which guarantee the quality of service (QoS) requirements are selected. For selecting the first relay which must detect both users’ signals, this process consists of the calculation of SINR for both users at each relay and comparing them with a predefined threshold. The computational complexity of SINR calculation is equal to \(8K\) in this case including three productions, three summations, and two divisions for each potential relay. Moreover, the complexity order of comparison with the predefined threshold for all potential relays is \({\mathcal{O}}\left( K \right)\) for each user. In the second stage, the relay with the best channel gain to the corresponding user is selected from the relays qualified in the first stage for each user. If we define the number of qualified relays for user1 as \(K_{1}\), and the number of qualified relays for user2 as \(K_{2}\), the complexity order of this process behaves as \({\mathcal{O}}\left( {K_{1} } \right)\) and \({\mathcal{O}}\left( {K_{2} } \right)\) for two users, respectively. Therefore, the total complexity of the proposed scheme in [21] can be presented as:

$$ complexity\;of\; scheme\; in\; [21] = 8K + {\mathcal{O}}(K) + {\mathcal{O}}(K) + {\mathcal{O}}(K_{1}) + {\mathcal{O}}(K_{2}) \approx {\mathcal{O}}(K) $$
(21)

It can be seen that the complexity order of the scheme in [21] is also linear in the number of potential relays. However, the complexity of this scheme is approximately similar to the proposed scheme. In addition, we investigate the proposed scheme in [25]. This scheme is also based on two-stage relay selection. The first stage is similar to the scheme in [21]. But, in the second stage the relays which cause maximum SINR at the corresponding users are selected. This means that we need to compute the obtained SINRs at users from relays which selected in the first stage (with complexity equal to \(4K_{1} \left( {K_{2} - 1} \right)\), where \(K_{1}\) and \(K_{2}\) are the number of qualified relays for user1 and user 2, respectively) and compare them with the predefined threshold (with the complexity order as \({\mathcal{O}}\left( {K_{1} K_{2} } \right)\)). It comes from the fact that the relays which detect the user1 signal definitely detect the signal of the second user (based on NOMA strategy). Hence, the relays that qualified for user1 in the first stage are a subset of relays that qualified for user2. Therefore, when we are investigating the condition of a relay qualified for user1, one of the potential relays qualified for user2 decreases. That’s why all possible cases are equal to \(K_{1} \left( {K_{2} - 1} \right)\) in the second stage. These values are also true for selecting the second relay. Therefore, the total complexity of the proposed scheme in [25] can be presented as:

$$ complexity \;of \;scheme \;in \left[ {25} \right] = 8K + {\mathcal{O}}\left( K \right) + {\mathcal{O}}\left( K \right) + 4K_{1} \left( {K_{2} - 1} \right) + {\mathcal{O}}\left( {K_{1} K_{2} } \right) + 4K_{1} \left( {K_{2} - 1} \right) + {\mathcal{O}}\left( {K_{1} K_{2} } \right) \approx {\mathcal{O}}\left( {K_{1} K_{2} } \right) $$
(22)

It is obvious that the complexity order of the scheme proposed in [25] is not linear in the number of potential relays. Hence, this scheme is more complicated than the other schemes reviewed or proposed in this paper.

Finally, we present the exhaustive search scheme that needs to investigate all possible cases for selecting the best relays. We know that this is an optimal scheme from the performance point of view. However, the complexity of exhaustive search is very high, especially for large networks. Hence, this is not a practical scheme, and we present that only for comparison. In the exhaustive search we must compute and compare all possible cases and then select the best case. In the previous schemes and after selecting the best relays, we apply the optimization algorithm just once to achieve the optimal power values. But, in the exhaustive search scheme it is needed to repeat the optimization algorithms for \(\left( {\begin{array}{*{20}c} K \\ 2 \\ \end{array} } \right)\) times (all possible cases that select two relays from \(K\) potential relays) and finally select the best two relays. As mentioned, we must implement the optimization problem for \(\left( {\begin{array}{*{20}c} K \\ 2 \\ \end{array} } \right) \approx {\mathcal{O}}\left( {K^{2} } \right)\) times and then apply the comparison operation in order of \({\mathcal{O}}\left( {K^{2} } \right)\) which show the exhaustive search is much more complex than the schemes investigated so far.

5 Results and Discussion

In the following, the performance of the proposed strategy in terms of sum-rate and energy efficiency is evaluated through numerical results. We consider a three-cell scenario with cooperative NOMA using the distributed potential relays in the main cell. Two other cells are considered as interfering cells. It is assumed that the BSs in each cell are located at the edge [40]. The potential relays in the main cell are uniformly deployed in a circular area between the BS and the cell-edge users. The path loss exponent is considered to be 2 and the noise power \(N_{0}\) is set to 0.01. The minimum target data rate (\(R_{i}^{min}\)) is the same for both users. In addition, the circuit power consumption is set to \(P_{c} = 0.1\) watts. In addition, it is assumed that the transmission power available at the relays is half of the transmission power available at the BS. It should be mentioned that the simulations are generated from 100,000 independent realizations of different channel conditions. Also, the iteration error tolerance \(\varepsilon\) is set to 0.001 for both the bisection and Dinkelbach methods.

Figure 2 depicts the comparison of the suggested method with the Max–Min relay selection, two-stage relay selection schemes in [21] and [25], and exhaustive search relay selection schemes in terms of sum rate over SNR with a cell radius of 50 m, considering two different numbers of potential relays. It should be noted that SNR is defined as the ratio of the available power at the BS to the noise power. The minimum target data rate is considered to be \(R_{i}^{min} = 1 bps/Hz\). As can be viewed from the figure, the proposed scheme considerably outperforms the Max–Min scheme and the proposed schemes in [21] and [25], especially when the number of potential relays increases. Also, the proposed scheme approximates the exhaustive search in both numbers of potential relays. It should be noted that the proposed relay selection method achieves this performance with much less complexity.

Fig. 2
figure 2

Comparison of the suggested method with the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] in terms of sum rate over SNR with cell radius of 50 m for two different number of potential relays and \(R_{i}^{min} = 1 bps/Hz\)

Full size image

In Fig. 3, we illustrate the sum-rate results versus the cell radius for the proposed scheme, Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25], where 4 potential relays are employed and SNR = 10 dB. The minimum target data rate is also set to \(R_{i}^{min} = 1 bps/Hz\). It is clear that the suggested method has superior performance compared to the Max–Min scheme and the schemes proposed in [21] and [25]. This superiority for a cell radius of 40 m over the Max–Min scheme, the scheme in [21], and the scheme in [25] approaches 100, 100, and 40%, respectively. Moreover, the performance of all schemes deteriorates gradually as the cell radius increases.

Fig. 3
figure 3

Sum rate versus the cell radius for the proposed scheme, Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] with 4 potential relays and \(R_{i}^{min} = 1 bps/Hz\)

Full size image

Figure 4 evaluates the comparison of the proposed method sum rate with the Max–Min method, the exhaustive search, and the methods proposed in [21] and [25] over SNR for different target rate values (\(R_{i}^{min} = 1 bps/Hz\) and \(R_{i}^{min} = 1.5 bps/Hz\)) with cell radius of 50 m, where the number of the potential relays is set to 4. Similar to the previous results, the proposed scheme achieves a better performance against all schemes except the exhaustive search, where with increasing the SNR values the performance gap between the proposed method and the Max–Min method and also two-stage relay selection methods is more obvious. Moreover, increasing the target rate values degrades the performance of all schemes by decreasing the feasibility probability of the optimization problem.

Fig. 4
figure 4

sum rate comparison of the proposed method with the Max–Min method, the exhaustive search, and the methods proposed in [21] and [25] over SNR for different target rate values with cell radius of 50 m and 4 potential relays

Full size image

Figures 5 and 6 depict the comparison of the proposed scheme with the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] in terms of energy efficiency over SNR with a cell radius of 50 m for 2 and 4 potential relays, respectively. It should be mentioned that the figures for different numbers of potential relays are shown separately for clarity and better comparison. Also, the minimum target data rate considered to be \(R_{i}^{min} = 1 bps/Hz\). When the number of potential relays is equal to 2, the proposed scheme achieves approximately the same performance as exhaustive search. However, when the number of potential relays is increased to 4, there is a small performance gap for some SNR values. It should be noted that, again, we achieve this performance with only one repetition of the optimization algorithm, whereas the exhaustive search repeats the algorithm \(K\left( {K - 1} \right)/2\) times, where \(K\) is the number of potential relays. It is clear that increasing the number of potential relays causes high complexity in the case of employing exhaustive search relay selection. On the other hand, we can see from Figs. 5 and 6 that the proposed scheme achieves considerably better performance than the other schemes, where this superiority increases with increasing the number of potential relays.

Fig. 5
figure 5

Comparison of the proposed method with the Max–Min method, the exhaustive search, and the methods proposed in [21] and [25] in terms of energy efficiency over SNR with cell radius of 50 m, 2 potential relays, and \(R_{i}^{min} = 1 bps/Hz\)

Full size image
Fig. 6
figure 6

Comparison of the proposed scheme with the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] in terms of energy efficiency over SNR with cell radius of 50 m, 4 potential relays, and \(R_{i}^{min} = 1 bps/Hz\)

Full size image

Figure 7 shows the energy efficiency performance over cell radius for the proposed scheme, Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] at SNR = 10 dB, where 4 potential relays are employed and \(R_{i}^{min} = 1 bps/Hz\). It can be seen that the suggested scheme has a superior performance compared to the Max–Min scheme and the schemes in [21] and [25], especially in the areas with a smaller cell radius. This superiority for a cell radius of 40 m over the Max–Min scheme, the scheme in [21], and the scheme in [25] approaches 110, 110, and 40%, respectively. Moreover, the performance of all schemes gradually deteriorates as the cell radius increases. Figure 8 evaluates the comparison of the sum-rate of the suggested scheme with the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] over SNR for different target rate values (\(R_{i}^{min} = 1 bps/Hz\) and \(R_{i}^{min} = 1.5 bps/Hz\)) with a cell radius of 50 m, where the number of the potential relay is set to 4. It is obvious that the suggested scheme obtains a better performance compared to other schemes except the exhaustive search, where with the decreasing the target rate value it can be seen that the suggested scheme at SNR = 8 dB outperforms the Max–Min scheme, the scheme in [21], and the scheme in [25] more than 90, 90, and 40%, respectively. Moreover, increasing the target rate values degrades the performance of all schemes, where the feasibility probability of the optimization problem decreases as the target data rate value increases.

Fig. 7
figure 7

Energy efficiency versus the cell radius for the suggested scheme, Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] with 4 potential relays and \(R_{i}^{min} = 1 bps/Hz\)

Full size image
Fig. 8
figure 8

Energy efficiency comparison of the suggested scheme with the Max–Min scheme, the exhaustive search, and the schemes proposed in [21] and [25] over SNR for different target rate values with cell radius of 50 m and 4 potential relays

Full size image

6 Conclusion

This paper investigated a three-cell communication network in which two adjacent cells affect the performance of the main cell with inter-cell interference. Employing HD cooperative NOMA, the BS in the main cell aims to broadcast the signals of its mobile users in two phases. The multiple potential relays are uniformly distributed in the main cell, while two users are located at far locations relative to the BS. In the first phase, the BS sends users’ signals to the potential relays based on the NOMA strategy, while in the second phase two selected relays simultaneously retransmit their corresponding users’ signals. We selected one relay per cell-edge user, which is for the first time in a multi-cell cooperative NOMA scenario. On the other hand, we proposed a novel relay selection criterion so that each selected relay signal not only experiences good channel conditions while the transmitting to its user, but also has as little impact as possible on the performance of the other user. Considering the inter-cell interference in the proposed model resulted in the addition of a new constraint to the optimization problems, which made the problems and their solutions more general. The sum-rate and energy efficiency maximization problems were presented, where both of which were non-convex, and we employed the transformation to relax them and make them convex. An iterative algorithm based on the bisection method was proposed to assign the power allocations for maximizing the sum-rate, while a three-stage bisection method in combination with the Dinkelbach algorithm was proposed to solve the energy efficiency optimization problem. The simulation results demonstrated that when the cell radius is set to 50 and the number of potential relays is set to 4, the proposed method significantly improves the system sum-rate and energy efficiency over the Max–Min relay selection method, the relay selection method in [21], and the relay selection method in [25] by more than 100, 100, and 40%, respectively. In addition, the proposed scheme achieves approximately the same performance as exhaustive search relay selection with a much lower order of complexity. It should be noted that the proposed scenario can be extended to a model with multiple selected relays and multiple cell-edge users by employing a new pairing strategy between cell-center relays and cell-edge users. In this paper, we presented a scenario with only two users. However, in the more realistic scenarios, the number of users is much more. Therefore, if we want to assign one relay per user in a dense scenario, maybe the exact scheme that was proposed in this paper is not a suitable criterion. In fact, it is possible and appropriate to use the concept of the proposed scheme, but we should propose a new scheme that considers the effect of each selected relay on more than one non-corresponding user, where the criterion should be modified and more general to achieve the best performance. Proposing a suitable modified scheme in the dense scenario (with more than two users) can show more the gain of our scheme compared the existing works. Moreover, defining a MIMO system model can be a more general future work with more challenging solutions.