Skip to main content
Springer Nature Link
Log in

TDOA and FDOA Hybrid Positioning of Mobile Radiation Source with Receiver Position Errors

  • Research
  • Published:
Wireless Personal Communications Aims and scope Submit manuscript

Abstract

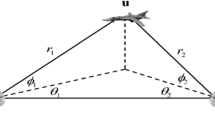
High-precision position awareness is essential to ubiquitous wireless networks, which can provide real-time position information and abundant status information for numerous practical applications. However, It is a challenge to obtain accurate position estimation utilizing traditional onefold parameter estimation, especially for the accurate position estimation of moving radiation source in the presence of receiver position errors. In this work, we developed an Improved Taylor Series estimation method in three-dimensional positioning scene, in which time difference of arrival (TDOA) and frequency difference of arrival (FDOA) are used to estimate the position and velocity of the target, and the position of the receiver is iteratively updated to reduce the influence of the receiver position errors. The closed-form expressions of Cramer–Rao low bound (CRLB) based on joint TDOA and FDOA positioning with receiver position errors are derived. In the simulation, CRLB with and without receiver position errors are evaluated to illustrate the influence of the receiver position errors on the positioning performance. Theory analysis and simulation results show that the proposed algorithm has lower complexity, smaller RMSE and better positioning performance than multidimensional scaling (W-MDS) algorithm, constrained total least squares algorithm and two-step weighted least squares algorithm for both near-field and far-field emitters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. Havyarimana, V., Xiao, Z., Semong, T., Bai, J., Chen, H., & Jiao, L. (2023). Achieving reliable intervehicle positioning based on redheffer weighted least squares model under Multi-GNSS outages. IEEE Transactions on Cybernetics, 53(2), 1039–1050.

    Google Scholar 

  2. Kang, Y., Wang, Q., Wang, J., & Chen, R. (2019). A high-accuracy TOA-based localization method without time synchronization in a three-dimensional space. IEEE Transactions on Industrial Informatics, 15(1), 173–182.

    Google Scholar 

  3. Xiao, Z., Chen, Y., Alazab, M., & Chen, H. (2022). Trajectory data acquisition via private car positioning based on tightly-coupled GPS/OBD integration in urban environments. IEEE Transactions on Intelligent Transportation Systems, 23(7), 9680–9691.

    Google Scholar 

  4. Mai, Z., Xiong, H., Yang, G., Zhu, W., He, F., Bian, R., & Li, Y. (2021). Mobile target localization and tracking techniques in harsh environment utilizing adaptive multi-modal data fusion. IET Communications, 15(5), 736–747.

    Google Scholar 

  5. Yan, K., Wu, H. C., Fang, S. H., Wang, C., Li, S., & Zhang, L. (2020). Indoor femtocell interference localization. IEEE Transactions on Wireless Communications, 19(8), 5176–5187.

    Google Scholar 

  6. Li, Y., & Yan, K. (2021). Indoor localization based on radio and sensor measurements. IEEE Sensors Journal, 21(22), 25 090-25 097.

    Google Scholar 

  7. Yan, K., Xia, Z., Wu, S., Liu, X., & Fang, G. (2022). Through-floor vital sign imaging for trapped persons based on optimized 2-D UWB life-detection radar deployment. IEEE Antennas and Wireless Propagation Letters, 21(1), 39–43.

    Google Scholar 

  8. Zhong, W., Xiong, H., Hua, Y., Shah, D. H., Liao, Z., & Xu, Y. (2024). TSFANet: Temporal-spatial feature aggregation network for GNSS jamming recognition. IEEE Transactions on Instrumentation and Measurement, 99, 1–13.

    Google Scholar 

  9. Xiong, H., Bian, R., Li, Y., Du, Z., & Mai, Z. (2020). Fault-tolerant GNSS/SINS/DVL/CNS integrated navigation and positioning mechanism based on adaptive information sharing factors. IEEE Systems Journal, 14(3), 3744–3754.

    Google Scholar 

  10. Havyarimana, V., Xiao, Z., Bizimana, P. C., Hanyurwimfura, D., & Jiang, H. (2021). Toward accurate intervehicle positioning based on GNSS pseudorange measurements under non-gaussian generalized errors. IEEE Transactions on Instrumentation and Measurement, 70, 1–12.

    Google Scholar 

  11. Shu, Y., Xu, P., Niu, X., Chen, Q., Qiao, L., & Liu, J. (2022). High-rate attitude determination of moving vehicles with GNSS: GPS, BDS, GLONASS, and Galileo. IEEE Transactions on Instrumentation Measurement, 71, 1–13.

    Google Scholar 

  12. Zhang, H., Xiong, H., Hao, S., Yang, G., Wang, M., & Chen, Q. (2024). A novel multidimensional hybrid position compensation method for INS/GPS integrated navigation systems during GPS outages. IEEE Sensors Journal, 24(1), 962–974.

    Google Scholar 

  13. Xiong, H., Tang, J., Xu, H., Zhang, W., & Du, Z. (2018). A robust single GPS navigation and positioning algorithm based on strong tracking filtering. IEEE Sensors Journal, 18(1), 290–298.

    Google Scholar 

  14. Havyarimana, V., Hanyurwimfura, D., Nsengiyumva, P., & Xiao, Z. (2018). A novel hybrid approach based-SRG model for vehicle position prediction in multi-GPS outage conditions. Information Fusion, 41, 1–8.

    Google Scholar 

  15. Havyarimana, V., Xiao, Z., Sibomana, A., Wu, D., & Bai, J. (2020). A fusion framework based on sparse Gaussian–Wigner prediction for vehicle localization using GDOP of GPS satellites. IEEE Transactions on Intelligent Transportation Systems, 21(2), 680–689.

    Google Scholar 

  16. He, Q., Hu, J., Blum, R. S., & Wu, Y. (2016). Generalized Cramer-Rao bound for joint estimation of target position and velocity for active and passive radar networks. IEEE Transactions on Signal Processing, 64(8), 2078–2089.

    MathSciNet  Google Scholar 

  17. Ma, F., Liu, Z., & Guo, F. (2020). Distributed direct position determination. IEEE Transactions on Vehicular Technology, 69(11), 14 007-14 012.

    Google Scholar 

  18. Sun, Y., Ho, K. C., & Wan, Q. (2019). Solution and analysis of TDOA localization of a near or distant source in closed form. IEEE Transactions on Signal Processing, 67(2), 320–335.

    MathSciNet  Google Scholar 

  19. Xiong, H., Peng, M., Gong, S., & Du, Z. (2018). A novel hybrid RSS and TOA positioning algorithm for multi-objective cooperative wireless sensor networks. IEEE Sensors Journal, 18(22), 9343–9351.

    Google Scholar 

  20. Ma, F., Liu, Z., & Guo, F. (2019). Direct position determination in asynchronous sensor networks. IEEE Transactions on Vehicular Technology, 68(9), 8790–8803.

    Google Scholar 

  21. Al Sadoon, M. . A. . G., Asif, R., Al Yasir, Y. . I. . A., Abd Alhameed, R. . A., & Excell, P. . S. (2020). AOA localization for vehicle-tracking systems using a dual-band sensor array. IEEE Transactions on Antennas and Propagation, 68(8), 6330–6345.

    Google Scholar 

  22. Li, Y. Y., Qi, G. Q., & Sheng, A. D. (2018). Performance metric on the best achievable accuracy for hybrid TOA/AOA target localization. IEEE Communications Letters, 22(7), 1474–1477.

    Google Scholar 

  23. Cao, H., Chan, Y. T., & So, H. C. (2020). Compressive TDOA estimation: Cramér-Rao bound and incoherent processing. IEEE Transactions on Aerospace and Electronic Systems, 56(4), 3326–3331.

    Google Scholar 

  24. Pei, Y., Li, X., Yang, L., & Guo, F. (2023). A closed-form solution for source localization using FDOA measurements only. IEEE Communications Letters, 27(1), 115–119.

    Google Scholar 

  25. Xiong, H., Peng, M., Zhu, K., Yang, Y., Du, Z., Xu, H., & Gong, S. (2018). Efficient bias reduction approach of time-of-flight-based wireless localization networks in NLOS states. IET Radar, Sonar & Navigation, 12(11), 1353–1360.

    Google Scholar 

  26. Wang, Y., & Ho, K. C. (2017). TDOA positioning irrespective of source range. IEEE Transactions on Signal Processing, 65(6), 1447–1460.

    MathSciNet  Google Scholar 

  27. Pine, K. C., Pine, S., & Cheney, M. (2021). The geometry of far-field passive source localization with TDOA and FDOA. IEEE Transactions on Aerospace and Electronic Systems, 57(6), 3782–3790.

    Google Scholar 

  28. Qu, X., Xie, L., & Tan, W. (2017). Iterative constrained weighted least squares source localization using TDOA and FDOA measurements. IEEE Transactions on Signal Processing, 65(15), 3990–4003.

    MathSciNet  Google Scholar 

  29. Ho, K. C., & Xu, W. (2004). An accurate algebraic solution for moving source location using TDOA and FDOA measurements. IEEE Transactions on Signal Processing, 52(9), 2453–2463.

    MathSciNet  Google Scholar 

  30. Wei, H. W., Peng, R., Wan, Q., Chen, Z. X., & Ye, S. F. (2010). Multidimensional scaling analysis for passive moving target localization with TDOA and FDOA measurements. IEEE Transactions on Signal Processing, 58(3), 1677–1688.

    MathSciNet  Google Scholar 

  31. Noroozi, A., Oveis, A. H., Hosseini, S. M., & Sebt, M. A. (2018). Improved algebraic solution for source localization from TDOA and FDOA measurements. IEEE Wireless Communications Letters, 7(3), 352–355.

    Google Scholar 

  32. Wang, Y., & Wu, Y. (2017). An efficient semidefinite relaxation algorithm for moving source localization using TDOA and FDOA measurements. IEEE Communications Letters, 21(1), 80–83.

    Google Scholar 

  33. Zhang, X., Wang, F., Li, H., & Himed, B. (2021). Maximum likelihood and IRLS based moving source localization with distributed sensors. IEEE Transactions on Aerospace and Electronic Systems, 57(1), 448–461.

    Google Scholar 

  34. Congfeng, L., Jinwei, Y., & Juan, S. (2020). Direct solution for fixed source location using well-posed TDOA and FDOA measurements. Journal of Systems Engineering and Electronics, 31(4), 666–673.

    Google Scholar 

  35. Ho, K. C. (2012). Bias reduction for an explicit solution of source localization using TDOA. IEEE Transactions on Signal Processing, 60(5), 2101–2114.

    MathSciNet  Google Scholar 

  36. Yang, B., Li, J., Shao, Z., & Zhang, H. (2023). Self-supervised deep location and ranging error correction for UWB localization. IEEE Sensors Journal, 23(9), 9549–9559.

    Google Scholar 

  37. Ho, K. C., Lu, X., & Kovavisaruch, L. (2007). Source localization using TDOA and FDOA measurements in the presence of receiver location errors: Analysis and solution. IEEE Transactions on Signal Processing, 55(2), 684–696.

    MathSciNet  Google Scholar 

  38. Noroozi, A., Sebt, M. A., & Oveis, A. H. (2019). Efficient weighted least squares estimator for moving target localization in distributed MIMO radar with location uncertainties. IEEE Systems Journal, 13(4), 4454–4463.

    Google Scholar 

  39. Yu, H., Gao, J., & Huang, G. (2012). Constrained total least-squares localisation algorithm using time difference of arrival and frequency difference of arrival measurements with sensor location uncertainties. IET Radar, Sonar and Navigation, 6(9), 891–899.

    Google Scholar 

  40. Mao, Z., Su, H., He, B., & Jing, X. (2021). Moving source localization in passive sensor network with location uncertainty. IEEE Signal Processing Letters, 28, 823–827.

    Google Scholar 

  41. Wang, W., Bai, P., Wang, Y., Liang, X., & Zhang, J. (2019). Optimal sensor deployment and velocity configuration with hybrid TDOA and FDOA measurements. IEEE Access, 7, 109181–109194.

    Google Scholar 

  42. Wang, D., Zhang, P., Yang, Z., Wei, F., & Wang, C. (2020). A novel estimator for TDOA and FDOA positioning of multiple disjoint sources in the presence of calibration emitters. IEEE Access, 8, 1613–1643.

    Google Scholar 

  43. Zou, Y., & Liu, H. (2020). TDOA localization with unknown signal propagation speed and sensor position errors. IEEE Communications Letters, 24(5), 1024–1027.

    Google Scholar 

Download references

Acknowledgements

The authors would like to thank the editors and the anonymous reviewers.

Funding

This work was supported in part by the Natural Science Foundation of Guangdong Province under Grant 2022A1515011975, in part by Shenzhen Fundamental Research Program under grant JCYJ20220530141017040, in part by the Natural Science Foundation of Shandong Province under grants ZR2022LZH005, in part by the Science and Technology Program in Qingdao under Grants 22-3-7-CSPZ-2-nsh.

Author information

Authors and Affiliations

  1. School of Information Science and Engineering, Shandong University, 266237, Qingdao, Shandong, China

    Yue Zhang, Fen He, Honglei Zhang, Hongliang Yang & Zhengfeng Du

  2. Shenzhen Research Institute of Shandong University, 518057, Shenzhen, China

    Yue Zhang & Fen He

  3. College of Computer Science and Electronic Engineering, Hunan University, 410082, Changsha, China

    Zhu Xiao

Authors
  1. Yue Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Fen He
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Honglei Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Hongliang Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Zhengfeng Du
    View author publications

    You can also search for this author inPubMed Google Scholar

  6. Zhu Xiao
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

YZ and FH designed the method and wrote the main part of the manuscript, HZ designed the experiments and contributed to the writing of the manuscript, HY conducted the complexity analysis of the algorithm, ZD and ZX made grammar modifications to the manuscript. All authors reviewed the manuscript.

Corresponding author

Correspondence to Fen He.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Y., He, F., Zhang, H. et al. TDOA and FDOA Hybrid Positioning of Mobile Radiation Source with Receiver Position Errors. Wireless Pers Commun 137, 199–220 (2024). https://doi.org/10.1007/s11277-024-11387-7

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11277-024-11387-7

Keywords