A generalized multi-skill aggregation method for cognitive diagnosis

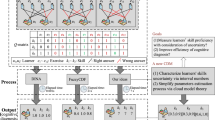
Abstract

Online education brings more possibilities for personalized learning, in which identifying the cognitive state of learners is conducive to better providing learning services. Cognitive diagnosis is an effective measurement to assess the cognitive state of students through response data of answering the problems(e.g., right or wrong). Generally, the cognitive diagnosis framework includes the mastery of skills required by a specified problem and the aggregation of skills. The current multi-skill aggregation methods are mainly divided into conjunctive and compensatory methods and generally considered that each skill has the same effect on the correct response. However, in practical learning situations, there may be more complex interactions between skills, in which each skill has different weight impacting the final result. To this end, this paper proposes a generalized multi-skill aggregation method based on the Sugeno integral (SI-GAM) and introduces fuzzy measures to characterize the complex interactions between skills. We also provide a new idea for modeling multi-strategy problems. The cognitive diagnosis process is implemented by a more general and interpretable aggregation method. Finally, the feasibility and effectiveness of the model are verified on synthetic and real-world datasets.

Appendix

The derivation of the latent response under three assumptions:

• Case 1. If $\alpha _{(1)^{\prime }}<\alpha _{(1)^{\prime \prime }}$, then

  • If $\alpha _{(k)}=\alpha _{(1)^{\prime }}$, then $X_1\subseteq L_k$ and $X_1\not \subseteq L_{k+1}$, thus $\mu (L_k)=1$. Since $\alpha _{(1)^{\prime }}<\alpha _{(1)^{\prime \prime }}$, $X_2\subseteq L_k$ and $X_2\subseteq L_{k+1}$. It is easy to show that the result is contrary to the (20), it does not meet the constraints.

  • Else if $\alpha _{(k)}=\alpha _{(1)^{\prime \prime }}$, then $X_2\subseteq L_k$, and $X_2\not \subseteq L_{k+1}$. As $\alpha _{(1)^{\prime }} < \alpha _{(1)^{\prime \prime }}$, we can infer that $X_1\not \subseteq L_k$ and $X_1\not \subseteq L_{k+1}$. Hence, we use $\alpha _{(k)}=\alpha _{(1)^{\prime \prime }}$ to substitute into the calculation formula, which satisfies the (20), that is $\mu (L_k)=1$ and $\mu (L_{k+1})=0$.

  Thus, the result of the latent response is given by $\eta =\alpha _{(k)}=\alpha _{(1)^{\prime \prime }}$, when $\alpha _{(1)^{\prime }}<\alpha _{(1)^{\prime \prime }}$.

• Case 2. If $\alpha _{(1)^{\prime }}=\alpha _{(1)^{\prime \prime }}$, in other words, $\alpha _{(k)}=\alpha _{(1)^{\prime }}=\alpha _{(1)^{\prime \prime }}$, then $X_1\subseteq L_k$, $X_2\subseteq L_k$, $X_1\not \subseteq L_{k+1}$ and $X_2\not \subseteq L_{k+1}$. This inference meets the constraints of (20), thus $\mu (L_k)=1$ and $\mu (L_{k+1})=0$ . Moreover, the latent response equals to $\eta =\alpha _{(k)}=\alpha _{(1)^{\prime }}=\alpha _{(1)^{\prime \prime }}$, when $\alpha _{(1)^{\prime }}=\alpha _{(1)^{\prime \prime }}$.

• Case 3. If $\alpha _{(1)^{\prime }}>\alpha _{(1)^{\prime \prime }}$, then

  • If $\alpha _{(k)}=\alpha _{(1)^{\prime }}$, then $X_1\subseteq L_k$, $X_1\not \subseteq L_{k+1}$. For $\alpha _{(1)^{\prime }}>\alpha _{(1)^{\prime \prime }}$, it is clear that $X_2\not \subseteq L_{k}$ and $X_2\not \subseteq L_{k+1}$. According to (20), we can conclude that $\mu (L_k)=1$. Moreover, the latent response is $\eta =\alpha _{(k)}=\alpha _{(1)^{\prime }}$.

  • Else if $\alpha _{(k)}=\alpha _{(1)^{\prime \prime }}$, then $X_2\subseteq L_k$, obviously, $X_2\not \subseteq L_{k+1}$. Since $\alpha _{(1)^{\prime }}>\alpha _{(1)^{\prime \prime }}$, we can infer that $X_1\not \subseteq L_k$ and $X_1\subseteq L_{k+1}$. Hence, it is impossible that make $\mu (L_k)=1$ and $\mu (L_{k+1})=0$. Hence, the latent response is computed by $\eta =\alpha _{(k)}=\alpha _{(1)^{\prime }}$ when $\alpha _{(1)^{\prime }}>\alpha _{(1)^{\prime \prime }}$.