Abstract
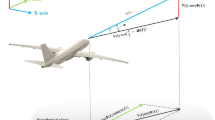
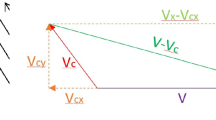
This paper is concerned with time-optimal navigation for flight vehicles in a planar, time-varying flow-field, where the objective is to find the fastest trajectory between initial and final points. The primary contribution of the paper is the observation that in a point-symmetric flow, such as inside vortices or regions of eddie-driven upwelling/downwelling, the rate of the steering angle has to be equal to one-half of the instantaneous vertical vorticity. Consequently, if the vorticity is zero, then the steering angle is constant. The result can be applied to find the time-optimal trajectories in practical control problems, by reducing the infinite-dimensional continuous problem to numerical optimization involving at most two unknown scalar parameters.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Acheson DJ (1990) Elementary fluid dynamics. Oxford University Press, Oxford
Bell DJ, Jacobson DH (1975) Singular optimal control problems. Academic Press, New York
Bellingham JG, Willcox JS (1996) Optimizing AUV oceanographic surveys. In: Proceedings of the 1996 symposium on autonomous underwater vehicle technology, 1996 (AUV ’96), June 1996, pp 391–398
Bryson AE, Ho YC (1975) Applied optimal control: optimization, estimation and control. Hemisphere Publishing Corporation, Washington
Cliff EM, Seywald H, Bless RR (1993) Hodograph analysis in aircraft trajectory optimization. In: AIAA guidance, navigation and control conference, pp. 363–371, Monterey, CA, 9–11 August 1993
Crassidis JL, Junkins JL (2004) Optimal estimation of dynamic systems. Chapman & Hall/CRC, Boca Raton
Ebbinghaus HD, Peckhaus V (2007) Ernst Zermelo: an approach to his life and work. Springer, Berlin
Eichhorn M (2010) Solutions for practice-oriented requirements for optimal path planning for the AUV “Slocum Glider”. In: IEEE oceans 2010, September 2010
Garau B, Alvarez A, Oliver G (2005) Path planning of autonomous underwater vehicles in current fields with complex spatial variability: an A* approach. In: Proceedings of the 2005 IEEE international conference on robotics and automation, 2005 (ICRA 2005). April 2005, pp 194–198
Karamcheti K (1996) Principles of ideal-fluid aerodynamics. Wiley, New York
Kirk DE (1970) Optimal control theory: an introduction. Dover Pulications, Mineola, New York
Knauss JA (2005) Introduction to physical oceanography, 2 edn. Waveland Press, Long Grove
Leitman G (1981) The calculus of variations and optimal control. Plenum Press, New York
Morrow M, Woolsey CA, Hagerman G (2006) Exploring Titan with autonomous, buoyancy-driven gliders. J Br Interplanet Soc 59(1): 27–34
Pamadi B (2004) Performance, stability, dynamics, and control of airplanes, 2nd edn. AIAA Education Series, Reston
Petrich J, Woolsey CA, Stilwell DJ (2009) Planar flow model identification for improved navigation of small AUVs. Ocean Engineering 36(1):119–131. Autonomous Underwater Vehicles
Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF (1963) The mathematical theory of optimal processes. Wiley, New York (translated by K. N. Trirogoff)
Rugh WJ (1996) Linear system theory. Prentice Hall, Upper Saddle River
Techy L, Woolsey CA (2009) Minimum-time path planning for unmanned aerial vehicles in steady uniform winds. AIAA J Guid Control Dyn 32(6): 1736–1746
Techy L, Woolsey CA, Morgansen KA (2010) Planar path planning for flight vehicles in wind with turn rate and acceleration bounds. In: International conference on robotics & automation, Anchorage, AK, May 2010
Vinh NX (1981) Optimal trajectories in atmospheric flight. Elsevier, New York
Zermelo E (1931) Über das Navigationsproblem bei ruhender oder veränderlicher Windverteilung. Zeitschrift für angewandte Mathematik und Mechanik 11(2): 114–124
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Techy, L. Optimal navigation in planar time-varying flow: Zermelo’s problem revisited. Intel Serv Robotics 4, 271–283 (2011). https://doi.org/10.1007/s11370-011-0092-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11370-011-0092-9