Abstract
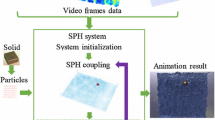
Hybrid approaches such as combining video data with pure physics-based simulation have been popular in the recent decade for computer graphics. The key motivation is to clearly retain salient advantages from both data-driven method and model-centric numerical simulation, while overcoming certain difficulties of both. The Eulerian method, which has been widely employed in flow simulation, stores variables such as velocity and density on regular Cartesian grids, thereby it could be associated with (volumetric) video data on the same domain. This paper proposes a novel method for flow simulation, which is tightly coupling video-based reconstruction with physically-based simulation and making use of meaningful physical attributes during re-simulation. First, we reconstruct the density field from a single-view video. Second, we estimate the velocity field using the reconstructed density field as prior. In the iterative process, the pressure projection can be treated as a physical constraint and the results of each step are corrected by obtained velocity field in the Eulerian framework. Third, we use the reconstructed density field and velocity field to guide the Eulerian simulation with anticipated new results. Through the guidance of video data, we can produce new flows that closely match with the real scene exhibited in data acquisition. Moreover, in the multigrid Eulerian simulation, we can generate new visual effects which cannot be created from raw video acquisition, with a goal of easily producing many more visually interesting results and respecting true physical attributes at the same time. We demonstrate salient advantages of our hybrid method with a variety of animation examples.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Ihmsen M, Orthmann J, Solenthaler B, Kolb A, Teschner M. SPH fluids in computer graphics. In Proc. Eurographics 2014 — State of the Art Reports, Apr. 2014.
Bridson R. Fluid Simulation for Computer Graphics. CRC Press, 2008.
Zuo Q, Qi Y, Qin H. A novel, integrated smoke simulation design method supporting local projection and guiding control over adaptive grids. The Visual Computer, 2013, 29(9): 883-892.
Zhang X, Bridson R, Greif C. Restoring the missing vorticity in advection-projection fluid solvers. ACM Transactions on Graphics, 2015, 34(4): 52:1-52:8.
Teng Y, Levin D I W, Kim T. Eulerian solid-fluid coupling. ACM Transactions on Graphics, 2016, 35(6): 1-8.
Okabe M, Dobashi Y, Anjyo K, Onai R. Fluid volume modeling from sparse multi-view images by appearance transfer. ACM Transactions on Graphics, 2015, 34(4): 93:1-93:10.
Gregson J, Ihrke I, Thuerey N, Heidrich W. From capture to simulation: Connecting forward and inverse problems in fluids. ACM Transactions on Graphics, 2014, 33(4): 70-79.
Zhai X, Hou F, Qin H, Hao A. Inverse modelling of incompressible gas flow in subspace. Computer Graphics Forum, 2017, 36(6): 100-111.
Quan H, Yu M, Song X, Gao Y. Real time reconstruction of fluid in video. International Journal of Modeling, Simulation, and Scientific Computing, 2013, 4(04): 1342001.
Ren B, Jiang Y, Li C, Lin M C. A simple approach for bubble modelling from multiphase fluid simulation. Computational Visual Media, 2015, 1(2): 171-181.
Wang C, Wang C, Qin H, Zhang T. Video-based fluid reconstruction and its coupling with SPH simulation. The Visual Computer, 2017, 33(9): 1211-1224.
Foster N, Metaxas D. Realistic animation of liquids. Graphical Models & Image Processing, 1996, 58(5): 471-483.
Müller M, Charypar D, Gross M. Particle-based fluid simulation for interactive applications. In Proc. the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, July 2003, pp.154-159.
Ihmsen M, Cornelis J, Solenthaler B, Horvath C, Teschner M. Implicit incompressible SPH. IEEE Transactions on Visualization & Computer Graphics, 2014, 20(3): 426-435.
Solenthaler B, Pajarola R. Predictive-corrective incompressible SPH. ACM Transactions on Graphics, 2009, 28(3): 1-6.
Schechter H, Bridson R. Ghost SPH for animating water. ACM Transactions on Graphics, 2012, 31(4): Article No. 61.
Wang X K, Ban X J, Zhang Y L, Liu S N, Ye P F. Surface tension model based on implicit incompressible smoothed particle hydrodynamics for fluid simulation. Journal of Computer Science and Technology, 2017, 32(6): 1186-1197.
Park S I, Kim M J. Vortex fluid for gaseous phenomena. In Proc. the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, July 2005, pp.261-270.
Macklin M. Position based fluids. ACM Transactions on Graphics, 2013, 32(32): 104:1-104:12.
Stam J. Stable fluids. In Proc. the 26th Annual Conference on Computer Graphics and Interactive Techniques, Aug. 1999, pp.121-128.
Zhu Y, Bridson R. Animating sand as a fluid. ACM Transactions on Graphics, 2005, 24(3): 965-972.
Batty C, Bertails F, Bridson R. A fast variational framework for accurate solid-fluid coupling. ACM Transactions on Graphics, 2007, 26(3): Article No. 100.
Losasso F, Fedkiw R. Simulating water and smoke with an octree data structure. ACM Transactions on Graphics, 2004, 23(3): 457-462.
Chentanez N, Mueller-Fischer M. A multigrid fluid pressure solver handling separating solid boundary conditions. IEEE Transactions on Visualization & Computer Graphics, 2012, 18(8): 1191-1201.
McAdams A, Sifakis E, Teran J. A parallel multigrid poisson solver for fluids simulation on large grids. In Proc. the 2010 ACM SIGGRAPH/Eurographics Symposium on Computer Animation, July 2010, pp.65-74.
Chentanez N. Real-time Eulerian water simulation using a restricted tall cell grid. ACM Transactions on Graphics, 2011, 30(4): Article No. 82.
Ihmsen M, Akinci N, Becker M, Teschner M. A parallel SPH implementation on multi-core CPUs. Computer Graphics Forum, 2011, 30(1): 99-112.
Ihrke I, Magnor M. Image-based tomographic reconstruction of flames. In Proc. the ACM SIGGRAPH/Eurographics Symposium on Computer Animation, August 2004, pp.365-373.
Atcheson B, Ihrke I, HeidrichW, Tevs A, Bradley D, Magnor M, Seidel H P. Time-resolved 3D capture of non-stationary gas flows. ACM Transactions on Graphics, 2008, 27(5): 1-9.
Gregson J, Krimerman M, Hullin M B, Heidrich W. Stochastic tomography and its applications in 3D imaging of mixing fluids. ACM Transactions on Graphics, 2012, 31(4): 1-10.
Liu Z, Hu Y, Qi Y. Modeling of smoke from a single view. In Proc. International Conference on Virtual Reality and Visualization, December 2011, pp.291-294.
Stephan W, Dirk L, Marcus M. Fast image-based modeling of astronomical nebulae. Computer Graphics Forum, 2013, 32(32): 93-100.
Keane R D, Adrian R J. Theory of crosscorrelation analysis of PIV images. Flow, Turbulence and Combustion, 1992, 49(3): 191-215.
Liu T, Shen L. Fluid flow and optical flow. Journal of Fluid Mechanics, 2008, 614(614): 253-291.
Kadri-Harouna S, Dérian P, Héas P, Mémin E. Divergence-free wavelets and high order regularization. International Journal of Computer Vision, 2013, 103(1): 80-99.
Zuo Q, Qi Y. A novel spatial-temporal optical flow method for estimating the velocity fields of a fluid sequence. The Visual Computer, 2017, 33(3): 293-302.
Kim B M, Liu Y, Llamas I, Rossignac J. FlowFixer: Using BFECC for fluid simulation. In Proc. Eurographics Conference on Natural Phenomena, Aug. 2005, pp.51-56.
Horn B K, Schunck B G. Determining optical flow. Artificial Intelligence, 1981, 17(1/2/3): 185-203.
Parikh N, Boyd S. Proximal algorithms. Foundations & Trends in Optimization, 2014, 1(3): 127-239.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
ESM 1
(PDF 108 kb)
Rights and permissions
About this article
Cite this article
Li, FY., Wang, CB., Qin, H. et al. Augmented Flow Simulation Based on Tight Coupling Between Video Reconstruction and Eulerian Models. J. Comput. Sci. Technol. 33, 452–462 (2018). https://doi.org/10.1007/s11390-018-1830-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11390-018-1830-7