Abstract
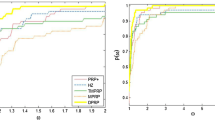
In this paper, the authors propose a class of Dai-Yuan (abbr. DY) conjugate gradient methods with linesearch in the presence of perturbations on general function and uniformly convex function respectively. Their iterate formula is x k+1 = x k + α k (s k + ω k ), where the main direction s k is obtained by DY conjugate gradient method, ω k is perturbation term, and stepsize α k is determined by linesearch which does not tend to zero in the limit necessarily. The authors prove the global convergence of these methods under mild conditions. Preliminary computational experience is also reported.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M. Al-Baali, Descent property and global convergence of the Fletcher-Reeves method with inexact line search, IMA J. Numer. Anal., 1985, 5(1): 121–124.
M. J. D. Powell, Restart procedures of the conjugate gradient method, Math. Program., 1997, 2: 241–245.
M. J. D. Powell, Non-convex minimization calculations and the conjugate gradient method, Lecture Notes in Math., Springer-Verlag, Berlin, 1984, 1066: 122–141.
Y. H. Dai and Y. Yuan, A nonlinear conjugate gradient method with a strong global convergence property, SIAM J. Optim., 1999, 10(1): 177–182.
Y. H. Dai and Y. Yuan, Some properties of a new conjugate gradient method, in Advances in Nonlinear Programing (ed. by Y. Yuan), Kluwer, Boston, 1998, 251–262.
B. T. Poljak and Y. Z. Tsypkin, Pseudogradient adaptation and training algorithms, Automat. Remote Control, 1973, 12: 83–94.
P. Tseng, Incremental gradient (-projection) method with momentum term and adaptive stepsize rule, SIAM J. on Optim., 1998, 8(2): 506–531.
A. A. Gaivoronski, Convergence properties of backpropagation for neural nets via theory of stochastic gradient methods, Part 1, Optim. Methods Software, 1994, 4(2): 117–134.
L. Grippo, A class of unconstrained minimization methods for neural network training, Optim. Methods Software, 1994, 4(2): 135–150.
O. L. Mangasarian and M. V. Solodov, Serial and parallel backpropagation convergence via nonmonotone perturbed minimization, Optim. Methods Software, 1994, 4(2): 103–116.
O. L. Mangasarian and M. V. Solodov, Backpropagation convergence via deternministic nonmonotone perturbed minimization, in Advances in Neural Information Processing Systems 6 (ed. by G. Tesauro, J. D. Cowan, and J. Alspector), Morgan Kaufmann, San Francisco, 1994, 383–390.
D. P. Bertsekas and J. N. Tsitsiklis, Gradient convergence in gradient methods with errors, SIAM J. Optim., 2000, 10(3): 627–642.
M. V. Solodov, Convergence analysis of perturbed feasible descent methods, J. Optim. Theory Appl., 1997, 93(2): 337–353.
M. V. Solodov, Incremental gradient algorithms with stepsizes bounded away from zero, Computational Optimization and Applications, 1998, 11: 23–35.
M. V. Solodov and B. F. Svaiter, Descent methods with linesearch in the presence of perturbations, Journal of Computational and Applied Mathematics, 1997, 80(2): 265–275.
Y. H. Dai, Further insight into the convergence of the Fletcher-Reeves method, Science in China, 1999, 42(9): 905–916.
Author information
Authors and Affiliations
Corresponding author
Additional information
The work is supported by the National Natural Science Foundation of China under Grant No. 10571106.
Rights and permissions
About this article
Cite this article
Wang, C., Li, M. Global Convergence of the Dai-Yuan Conjugate Gradient Method with Perturbations. Jrl Syst Sci & Complex 20, 416–428 (2007). https://doi.org/10.1007/s11424-007-9037-y
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s11424-007-9037-y