Abstract
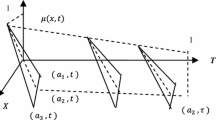
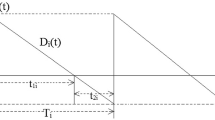
This paper considers the economic production quantity (EPQ) problem with backorder in which the setup cost, the holding cost and the backorder cost are characterized as fuzzy variables, respectively. Following expected value criterion and chance constrained criterion, a fuzzy expected value model (EVM) and a chance constrained programming (CCP) model are constructed. Then fuzzy simulations are employed to estimate the expected value of fuzzy variable and α-level minimal average cost. In order to solve the CCP model, a particle swarm optimization (PSO) algorithm based on the fuzzy simulation is designed. Finally, the effectiveness of PSO algorithm based on the fuzzy simulation is illustrated by a numerical example.
Similar content being viewed by others
References
G. Hadley and T. Whitin, Analysis of Inventory Systems, Prentice-Hall, Englewood Cliffs, NJ, 1963.
S. K. J. Chang, J. P. C. Chuang, and H. J. Chen, Short comments on technical note—The EOQ and EPQ models with shortages derived without derivatives, International Journal of Production Economics, 2005, 97(2): 241–243.
R. Ronald, G. K. Yang, and P. Chu, Technical note—The EOQ and EPQ models with shortages derived without derivatives, International Journal of Production Economics, 2004, 92(2): 197–200.
M. J. Rosenblatt and H. L. Lee, Economic production cycles with imperfect production processes, IIE Transactions, 1986, 18(1): 48–55.
Z. T. Balkhi and L. Benkherouf, A prodution lot size inventory model for deteriorating items and arbitrary production and demand rates, European Journal of Operational Research, 1996, 92(2): 302–309.
S. Sana, S. K. Goyal, and K. S. Chaudhuri, A production-inventory model for a deteriorating item with trended demand and shortages, European Journal of Operational Research, 2004, 157(2): 357–371.
H. Lee and J. S. Yao, Economic production quantity for fuzzy demand quantity and fuzzy production quantity, European Journal of Operational Research, 1998, 109(1): 203–211.
S. C. Chang, Fuzzy production inventory for fuzzy product quantity with triangular fuzzy number, Fuzzy Sets and Systems, 1999, 107(1): 37–57.
D. Lin and J. S. Yao, Fuzzy economic production for production inventory, Fuzzy Sets and Systems, 2000, 111(3): 465–495.
C. H. Hsieh, Optimization of fuzzy production inventory models, Information Sciences, 2002, 146(1–4): 29–40.
L. A. Zadeh, Fuzzy set as a basis for a theory of possibility, Fuzzy Sets and Systems, 1978, 1: 3–28.
D. Dubois and H. Prade, Possibility Theory: An Approach to Computerized Processing of Uncertainty, Plenum, New York, 1988.
R. R. Yager, On the completion of qualitative possibility measures, IEEE Transactions on Fuzzy Systems, 1993, 1(3): 184–194.
B. Liu and Y. K. Liu, Expected value of fuzzy variable and fuzzy expected value models, IEEE Transactions on Fuzzy Systems, 2002, 10(4): 445–450.
B. Liu, Uncertainty Theory: An Introduction to its Axiomatic Foundations, Springer-Verlag, Berlin, 2004.
B. Liu, Theory and Practice of Uncertain Programming, Physica-Verlag, Heidelberg, 2002.
B. Liu, A survey of credibility theory, Fuzzy Optimization and Decision Making, 2006, 5(4): 387–408.
Y. K. Liu and B. Liu, Expected value operator of random fuzzy variable and random fuzzy expected value models, International Jorunal of Uncertainty, Fuzziness & Knowledge-Based Systems, 2003, 11(2): 195–215.
R. Q. Zhao, W. S. Tang, and H. L. Yun, Fuzzy renewal process, fuzzy renewal reward process and their applications, IEEE International Conference on Fuzzy Systems, 2004, 2: 739–744.
T. Bäck, D. B. Fogel, and Z. Michalewicz, Handbook of Evolutionary Computation, IOP Publishing and Oxford University Press, New York, 1997.
D. E. Goldberg, Genetic Algorithms in Search, Optimization and Machine Learning, MA: Addison-Wesley, 1989.
J. Kennedy and R. Eberhart, Particle swarm optimization, IEEE International Conference on Neural Networks, 4: 1995, 1942–1948.
J. Kennedy, R. Eberhart, and Y. Shi, Swarm Intelligence, Morgan Kaufmann Publishers, San Francisco, 2001.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research is supported by the National Natural Science Foundation of China under Grant No. 70471049.
Rights and permissions
About this article
Cite this article
Wang, X., Tang, W. Fuzzy EPQ inventory models with backorder. J Syst Sci Complex 22, 313–323 (2009). https://doi.org/10.1007/s11424-009-9166-6
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-009-9166-6