Abstract
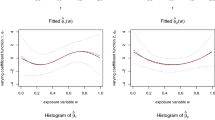
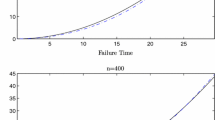
Current status data often arise in survival analysis and reliability studies, when a continuous response is reduced to an indicator of whether the response is greater or less than an observed random threshold value. This article considers a partial linear model with current status data. A sieve least squares estimator is proposed to estimate both the regression parameters and the nonparametric function. This paper shows, under some mild condition, that the estimators are strong consistent. Moreover, the parameter estimators are normally distributed, while the nonparametric component achieves the optimal convergence rate. Simulation studies are carried out to investigate the performance of the proposed estimates. For illustration purposes, the method is applied to a real dataset from a study of the calcification of the hydrogel intraocular lenses, a complication of cataract treatment.
Similar content being viewed by others
References
A. K. F. Yu, K. Y. W. Kwan, D. H. Y. Chan, et al., Clinical features of 46 eyes with calcified hydrogel intraocular lenses, Journal of Cataract and Refractive Surgery, 2001, 27: 1596–1606.
H. Xue, K. F. Lam, and G. Li, Sieve maximum likelihood estimator for semiparametric regression models with current status data, Journal American Statistical Association, 2004, 99: 346–356.
J. Huang and A. J. Rossini, Sieve estimation for the proportional odds failure-time regression model with interval censoring, Journal of American Statistical Association, 1997, 92: 960–967.
P. J. Bickel, C. A. J. Klaassen, Y. Ritov, et al., Efficient and Adaptive Estimation for Semiparametric Models, Johns Hopkins University Press, Baltimore, 1993.
S. Ma and M. R. Kosorok, Robust semiparametric M-estimation and the weighted bootstrap, Journal of Multivariate Analysis, 2005, 96: 190–217.
S. Ma, Semiparametric regression with current status data, Far East Journal of Theoretical Statistics, 2005, 15: 53–73.
A. W. van der Vaart and J. A. Wellner, Weak Convergence and Empirical Processes, Springer-Verlag, New York, 1996.
H. Xue, K. F. Lam, B. J. Cowling, et al., Semi-parametric accelerated failure time regression analysis with application to interval-censored HIV/AIDS data, Statistics in Medicine, 2006, 25: 3850–3863.
K. F. Lam and H. Xue, A semiparametric regression cure model with current status data, Biometrika, 2005, 92: 573–586.
X. Shen and W. H. Wong, Convergence rate of sieve estimates, The Annals of Statistics, 1994, 22: 680–615.
J. Huang, Efficient estimation for the proportional hazards model with interval censoring, The Annals of Statistics, 1996, 24: 540–568.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research is supported in part by the National Natural Science Foundation of China under Grant No. 10801133.
This paper was recommended for publication by Editor Guohua ZOU.
Rights and permissions
About this article
Cite this article
Wang, S., Zhang, S. & Xue, H. Sieve least squares estimator for partial linear models with current status data. J Syst Sci Complex 24, 335–346 (2011). https://doi.org/10.1007/s11424-011-8050-3
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-011-8050-3