Abstract
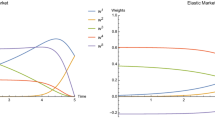
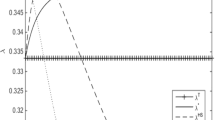
This paper develops a sequential fair Stackelberg auction model in which each of the two risk-seeking insiders has an equal chance to be a leader or follower at each auction stage. The authors establish the existence, uniqueness of sequential fair Stackelberg equilibria (in short, FSE) when both insiders adopt linear strategies, and find that at the sequential equilibria such two insiders compete aggressively that cause the liquidity of market to drop, the information to be revealed and the profit to go down very rapidly while the trading intensity goes substantially high. Furthermore, the authors also give continuous versions of corresponding parameters in the sequential FSE in closed forms, as the time interval between auctions approaches to zero. It shows that such parameters go down or up approximately exponentially and all of the liquidity of market, information and profit become zero while the trading intensity goes to infinity. Some numerical simulations about the sequential FSE are also illustrated.
Similar content being viewed by others
References
Kyle A S, Continuous auctions and insider trading, Econometrica, 1985, 53: 1315–1335.
Kyle A S and Wang F A, Speculation duopoly with agreement todisagree: Can overconfidence survive the market test?, Journal of Finance, 1997, 52: 2073–2090.
Jain N and Mirman L, Insider trading with correlated signals, Economics Letters, 1999, 65: 105–133.
Luo S, The impact of public information on insider trading, Economics Letters, 2001, 112: 59–68.
Zhang W D, Impact of outsiders and disclosed insider trades, Financ. Res. Lett., 2008, 5: 137–145.
Liu H and Zhang W D, Insider trading with public and shared information, Economic Modelling, 2008, 28: 1756–1762.
Aase K K, Bjuland T, and Øksendal B, Partially informed noise traders, Math. Finan. Econ., 2012, 6: 93–104.
Zhou D, Overconfidence on public information, Economics Letters, 2011, 112: 239–242.
Zhou D Q, The virtue of overconfidence when you are not perfectly informed, Economic Modelling, 2015, 47: 105–110.
Du S and Liu H, The overconfident trader does not always overreact to his information, Economic Modelling, 2015, 46: 384–390.
Holden C W and Subrahmanyam A, Long-lived private information and imperfect competition, Journal of Finance, 1992, 47: 247–270.
Jain N and Mirman L, Real and financial effects of insider trading with correlated signals, Economic Theory, 2000, 16: 333–353.
Daher W and Mirman L, Cournot duopoly and insider trading with two insiders, The Quarterly Review of Economics and Finance, 2006, 46: 530–551.
Jain N and Mirman L, Effects of insider trading under different market structures, The Quarterly Review of Economics and Finance, 2002, 42: 19–39.
Daher W and Mirman L, Market structure and insider trading, International Review of Economics and Finance, 2007, 16: 306–331.
Daher W, Karam F, and Mirman L J, Insider trading with different market structures, International Review of Economics and Finance, 2012, 24: 143–154.
Wang L F S and Wang Y C, Stackelberg real-leader in an insider trading model, Studies in Economics and Finance, 2010, 27: 30–46.
Wang L F S, Wang Y C, and Ren S, Stackelberg financial-leader in insider trading model, International Review of Economics and Finance, 2009, 18: 123–131.
Back K and Pedersen H, Long-lived information and intraday patterns, Journal of Financial Markets, 1998, 1: 385–402.
Gong F Z and Zhou D Q, Insider trading in the market with rational expected price, arXiv: 1012.2160v1 [q-fin.TR], 2010.
Gong F Z and Liu H, The mixed equilibrium of insider trading in the market with rational expected price, Chapter 11 in Stochastic Analysis and Applications to Finance, Edited by Zhang T and Zhou X, World Scientific, 2012, 197–223.
Zhou Y H, Existence of linear strategy equilibrium in insider trading with partial observations, Journal of System Science & Complexity, 2016, 29(5): 1281–1292.
Aumann R J, Backward induction and common knowledge of rationality, Games and Economic Behavior, 1995, 8: 6–19.
Kreps D and Wilson R, Sequential equilibria, Econometrica, 1982, 50: 863–984.
Osborne M J and Rubinstein A, A Course in Game Theory, Cambridge, MIT, 1994.
Graybill F A, An Introduction to Linear Statistical Models (I), McGraw-Hill, New York, 1961.
Author information
Authors and Affiliations
Corresponding author
Additional information
The first author is supported by the National Natural Science Foundation of China under Grant No. 10721101 and China’s National 973 Project (2006CB805900). The second author is supported by the National Natural Science Foundation of China under Grant Nos. 11161011 and 11365005, Guizhou EDKY[2016]027, Guizhou QKZYD[2016]4006 and Guizhou ZDXK[2016]8.
This paper was recommended for publication by Editor WANG Shouyang.
Rights and permissions
About this article
Cite this article
Gong, F., Zhou, Y. Sequential Fair Stackelberg Equilibria of Linear Strategies in Risk-Seeking Insider Trading. J Syst Sci Complex 31, 1302–1328 (2018). https://doi.org/10.1007/s11424-018-6266-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-018-6266-1