Abstract
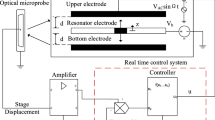
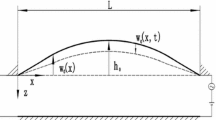
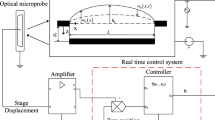
This paper addresses a nonlinear feedback control problem for the chaotic arch microelectro- mechanical system with unknown parameters, immeasurable states and partial state-constraint subjected to the distributed electrostatic actuation. To reflect inherent properties and design controller, the phase diagrams, bifurcation diagram and Poincare section are presented to investigate the nonlinear dynamics. The authors employ a symmetric barrier Lyapunov function to prevent violation of constraint when the arch micro-electro-mechanical system faces some limits. An RBF neural network system integrating with an update law is adopted to estimate unknown function with arbitrarily small error. To eliminate chaotic oscillation, a neuro-adaptive backstepping control scheme fused with an extended state tracking differentiator and an observer is constructed to lower requirements on measured states and precise system model. Besides, introducing an extended state tracking differentiator avoids repeated derivative for the virtual control signal associated with conventional backstepping. Finally, simulation results are presented to illustrate feasibility of the proposed scheme.
Similar content being viewed by others
References
Haghighi H S and Markazi A H D, Chaos prediction and control in MEMS resonators, Communications in Nonlinear Science and Numerical Simulation, 2010, 15(10): 3091–3099.
Ghanbari A and Moghanni-Bavil-Olyaei M, Adaptive fuzzy terminal sliding-mode control of MEMS z-axis gyroscope with extended Kalman filter observer, Systems Science and Control Engineering, 2014, 2(1): 183–191.
Perez-Molina M and Prez-Polo MF, Fold-Hopf bifurcation, steady state, self-oscillating and chaotic behavior in an electromechanical transducer with nonlinear control, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(12): 5172–5188.
Luo S, Sun Q, and Cheng W, Chaos control of the micro-electro-mechanical resonator by using adaptive dynamic surface technology with extended state observer, AIP Advances, 2016, 6(4): 045104.
Zeng X and Jiang H, Liquid Tunable Microlenses based on MEMS techniques, Journal of Physics D, 2013, 46(32): 474–480.
Das K and Batra R, Pull-in and snap-through instabilities in transient deformations of microelectromechanical systems, Journal of Micromechanics and Microengineering, 2009, 19(3): 035008.
Younis M I, Ouakad H M, Alsaleem F M, et al., Nonlinear dynamics of MEMS arches under harmonic electrostatic actuation, Journal of Microelectromechanical Systems, 2010, 19(3): 647–656.
Tajaddodianfar F, Yazdi M R H, Pishkenari H N, et al., Classification of the nonlinear dynamics in an initially curved bistable micro/nano-electro-mechanical system resonator, Micro and Nano Letters, 2015, 10(10): 583–588.
Tajaddodianfar F, Pishkenari H N, and Yazdi M R H, Prediction of chaos in electrostatically actuated arch micro-nano resonators: Analytical approach, Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1): 182–195.
Mayoof F N and Hawwa M A, Chaotic behavior of a curved carbon nanotube under harmonic excitation, Chaos, Solitons and Fractals, 2009, 42(3): 1860–1867.
Nayfeh A, Ouakad H, Najar F, et al., Nonlinear dynamics of a resonant gas sensor, Nonlinear Dynamics, 2010, 59(4): 607–618.
Miandoab E M, Pishkenari H N, Yousefi-Koma A, et al., Chaos prediction in MEMS-NEMS resonators, International Journal of Engineering Science, 2014, 82(3): 74–83.
Alasty A and Salarieh H, Controlling the chaos using fuzzy estimation of OGY and Pyragas controllers, Chaos, Solitons and Fractals, 2005, 26(2): 379–392.
Ho M C, Hung Y C, and Jiang I M, Synchronization between two chaotic systems with different order by using active control, International Journal of Nonlinear Sciences and Numerical Simulation, 2005, 6(3): 249–254.
Yassen M, Controlling chaos and synchronization for new chaotic system using linear feedback control, Chaos, Solitons and Fractals, 2005, 26(3): 913–920.
Shang F, Liu Y, and Zhang C, Adaptive practical tracking control by output feedback for a class of nonlinear systems, Journal of Systems Science and Complexity, 2010, 23(6): 1210–1220.
Sun Z, Xu W, Yang X, et al., Inducing or suppressing chaos in a double-well Duffing oscillator by time delay feedback, Chaos, Solitons and Fractals, 2006, 27(3): 705–714.
Roopaei M, Jahromi M Z, and Jafari S, Adaptive gain fuzzy sliding mode control for the synchronization of nonlinear chaotic gyros, Chaos, 2009, 19(1): 377–411.
Yang G, Kao Y, and Li W, Sliding mode control for Markovian switching singular systems with time-varying delays and nonlinear perturbations, Discrete Dynamics in Nature and Society, 2013, 2013: 77–80.
Liu L, Fu Z, and Song X, An adaptive sliding mode control of delta operator systems with input nonlinearity containing unknown slope parameters, Journal of Systems Science and Complexity, 2016, 30(3): 1–15.
Batur C, Sreeramreddy T, and Khasawneh Q, Sliding mode control of a simulated MEMS gyro scope, ISA Transactions, 2006, 45(1): 99–108.
Fei J and Batur C, A novel adaptive sliding mode control with application to MEMS gyroscope, ISA Transactions, 2009, 48(1): 73–78.
Zhankui S and Sun K, Nonlinear and chaos control of a micro-electro-mechanical system by using second-order fast terminal sliding mode control, Communications in Nonlinear Science and Numerical Simulation, 2013, 18(9): 2540–2548.
Li Y, Tong S, and Li T, Adaptive fuzzy backstepping control of static VAR compensator based on state observer, Nonlinear Dynamics, 2013, 73(1–2): 133–142.
Chen Q, Tao L, and Nan Y, Full-order sliding mode control for high-order nonlinear system based on extended state observer, Journal of Systems Science and Complexity, 2016, 29(4): 978–990.
Reif K and Unbehauen R, The extended Kalman filter as an exponential observer for nonlinear systems, IEEE Transactions on Automatic Control, 1999, 47(8): 2324–2328.
Zhou J, Wen C, and Zhang Y, Adaptive output control of nonlinear systems with uncertain dead-zone nonlinearity, IEEE Transactions on Automatic Control, 2006, 51(3): 504–511.
Sun G, Ren X, and Li D, Neural active disturbance rejection output control of multimotor servomechanism, IEEE Transactions on Control Systems Technology, 2015, 23(2): 746–753.
Tee K P, Ge S S, and Tay E H, Barrier Lyapunov functions for the control of output-constrained nonlinear systems, Automatica, 2009, 45(4): 918–927.
Wu J, Chen W, Yang F, et al., Global adaptive neural control for strict-feedback time-delay systems with predefined output accuracy, Information Sciences, 2015, 301(C): 27–43.
Yau H T, Wang C C, Hsieh C T, et al., Nonlinear analysis and control of the uncertain microelectro- mechanical system by using a fuzzy sliding mode control design, Computers and Mathematics with Applications, 2011, 61(8): 1912–1916.
Chen Q, Tang X, Nan Y, et al., Finite-time neural funnel control for motor servo systems with unknown input constraint, Journal of Systems Science and Complexity, 2017, 30(3): 579–594.
Tajaddodianfar F, Pishkenari H N, Yazdi M R H, et al., Size-dependent bistability of an electrostatically actuated arch NEMS based on strain gradient theory, Journal of Physics D, 2015, 48(24): 245503.
Li Y, L¨u H, and Jiao D, Prescribed performance synchronization controller design of fractionalorder chaotic systems: An adaptive neural network control approach, AIP Advances, 2017, 7(3): 035106.
Luo S and Song Y, Chaos analysis-based adaptive backstepping control of the microelectromechanical resonators with constrained output and uncertain time delay, IEEE Transactions on Industrial Electronics, 2016, 63(10): 6217–6225.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the National Natural Science Foundation of China under Grant Nos. 51505170, 51475097 and 51505045, Basic and Frontier Research Program of Chongqing Municipality under Grant Nos. cstc2016jcyjA0584 and cstc2016jcyjA0441), Project of Introduction of Talents of Guizhou University (No. [2017]27) and Key Scientific Research Program of Guizhou Province under Grant No. [2017]3001).
This paper was recommended for publication by Editor LIU Yungang.
Rights and permissions
About this article
Cite this article
Luo, S., Li, S. & Tajaddodianfar, F. Chaos and Nonlinear Feedback Control of the Arch Micro-Electro-Mechanical System. J Syst Sci Complex 31, 1510–1524 (2018). https://doi.org/10.1007/s11424-018-7234-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-018-7234-5