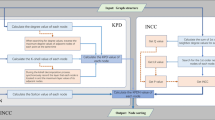
Abstract
Finding out the key node sets that affect network robustness has great practical significance for network protection and network disintegration. In this paper, the problem of finding key node sets in complex networks is defined firstly. Because it is an NP-hard combinatorial optimization problem, discrete fireworks algorithm is introduced to search the optimal solution, which is a swarm intelligence algorithm and is improved by the prior information of networks. To verify the effect of improved discrete fireworks algorithm (IDFA), experiments are carried out on various model networks and real power grid. Results show that the proposed IDFA is obviously superior to the benchmark algorithms, and networks suffer more damage when the key node sets obtained by IDFA are removed from the networks. The key node sets found by IDFA contain a large number of non-central nodes, which provides the authors a new perspective that the seemingly insignificant nodes may also have an important impact on the robustness of the network.
Similar content being viewed by others
References
Chen G R, Wang X F, and Li X, Introduction to Complex Networks Models, Structures and Dynamics, Higher Education Press, Beijing, 2015.
Cui P, Zhu P, Wang K, et al., Enhancing robustness of interdependent network by adding connectivity and dependence links, Physica A: Statistical Mechanics and Its Applications, 2018, 497: 185–197.
Chen Z, Wu J, Xia Y, et al., Robustness of interdependent power grids and communication networks: A complex network perspective, IEEE Transactions on Circuits & Systems II Express Briefs, 2017, 99: 115–119.
Liu J, Jiang Z Y, Kato N, et al., Reliability evaluation for NFV deployment of future mobile broadband networks, IEEE Wireless Communications, 2016, 23(3): 90–96.
Freeman L C, A set of measures of centrality based on betweenness, Sociometry, 1977, 40(1): 35–41.
Stella M and Domenico M D, Distance entropy cartography characterises centrality in complex networks, Entropy, 2018, 20(4): 268–279.
Borgatti S P, Centrality and network flow, Social Networks, 2005, 27(1): 55–71.
Kitsak M, Gallos L K, and Havlin S, Identification of influential spreaders in complex networks, Nature Physics, 2010, 6: 888–893.
Brin S and Page L, The anatomy of a large-scale hypertextual web search engine, Computer Networks and ISDN Systems, 1998, 30: 107–117.
Wang J, Hou X, Li K, et al., A novel weight neighborhood centrality algorithm for identifying influential spreaders in complex networks, Physica A: Statistical Mechanics & Its Applications, 2017, 475: 88–105.
Jiang Z Y and Ma J F, Deployment of check-in nodes in complex networks, Scientific Reports, 2017, 7: 40428.
Deng Y, Wu J, Xiao Y, et al., Efficient disintegration strategies with cost constraint in complex networks: The crucial role of nodes near average degree, Chaos, 2018, 28: 061101.
Li Y P, Tan S Y, Deng Y, et al., Attacker-defender game from a network science perspective, Chaos, 2018, 28: 051102.
Li J, Wu J, Li Y, et al., Optimal attack strategy in random scale-free networks based on incomplete information, Chinese Physics Letters, 2011, 6: 068902.
Deng Y, Wu J, Tan Y J, Optimal attack strategy of complex networks based on tabu search, Physica A: Statistical Mechanics and Its Applications, 2016, 442: 74–81.
Ma Q and Ma J, Identifying and ranking influential spreaders in complex networks with consideration of spreading probability, Physica A: Statistical Mechanics and Its Applications, 2017, 465: 312–330.
Nguyen D, Nguyen T, Do T, et al., Probability-based multi-hop diffusion method for influence maximization in social networks, Wireless Personal Communications, 2017, 93(4): 903–916.
Tan Y and Zhu Y, Fireworks algorithm for optimization, Lecture Notes in Computer Science, 2010, 6145: 355–364.
Tan Y, Fireworks Algorithm, Springer, Heidelberg, 2015.
Tan Y and Zheng S Q, Recent advance in fireworks algorithm, CAAI Transactions on Intelligent Systems, 2014, 9(5): 516–528.
Majdouli, M A E, and Imrani A A E, Discrete fireworks algorithm for single machine scheduling problems, International Journal of Applied Metaheuristic Computing, 2016, 7(3): 24–35.
Xue J J, Wang Y, Li H, et al., Discrete fireworks algorithm for aircraft mission planning, Lecture Notes in Computer Science, 2016, 9712: 544–551.
Liu F Z, Xiao B, Li H, et al., Discrete fireworks algorithm for clustering in wireless sensor networks, Lecture Notes in Computer Science, 2018, 10941: 273–282.
Latora V and Mauchiori M, A measure of centrality based on network efficiency, New Journal of Physics, 2007, 9(6): 188–198.
Erdős P and Rényi A, On the evolution of random graphs, Publications of the Mathematical Institude of the Hungarian Academy of Science, 1960, 5: 17–60.
Barabási A L and Albert R, Emergence of scaling in random networks, Science, 1999, 286(5439): 509–512.
Goh K I, Kahng B, and Kim D, Universal behavior of load distribution in scale-free networks, Physical Review Letters, 2001, 87(27): 278701.
Liu H L, Ma C, Xiang B B, et al., Identifying multiple influential spreaders based on generalized closeness centrality, Physica A: Statistical Mechanics and Its Applications, 2018, 492: 2237–2248.
Watts D J and Strogatz S H, Collective dynamics of small-world networks, Nature, 1998, 393(6684): 440–442.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was supported by the National Natural Science Foundation of China under Grant No. 61502522.
This paper was recommended for publication by Editor SUN Jian.
Rights and permissions
About this article
Cite this article
Liu, F., Xiao, B. & Li, H. Finding Key Node Sets in Complex Networks Based on Improved Discrete Fireworks Algorithm. J Syst Sci Complex 34, 1014–1027 (2021). https://doi.org/10.1007/s11424-020-9023-1
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-020-9023-1