Abstract
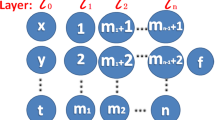
This paper extends a method, called bilinear neural network method (BNNM), to solve exact solutions to nonlinear partial differential equation. New, test functions are constructed by using this method. These test functions are composed of specific activation functions of single-layer model, specific activation functions of “2-2” model and arbitrary functions of “2-2-3” model. By means of the BNNM, nineteen sets of exact analytical solutions and twenty-four arbitrary function solutions of the dimensionally reduced p-gBKP equation are obtained via symbolic computation with the help of Maple. The fractal solitons waves are obtained by choosing appropriate values and the self-similar characteristics of these waves are observed by reducing the observation range and amplifying the partial picture. By giving a specific activation function in the single layer neural network model, exact periodic waves and breathers are obtained. Via various three-dimensional plots, contour plots and density plots, the evolution characteristic of these waves are exhibited.
Similar content being viewed by others
References
Liu Y P, Liao S J, and Li Z B, Symbolic computation of strongly nonlinear periodic oscillations, Journal of Symbolic Computation, 2013, 55: 72–95.
Feng R Y and Gao X S, Rational general solutions of algebraic ordinary differential equations, Proceedings of the 2004 International Symposium on Symbolic and Algebraic Computation (ISSAC’04), Ed. by Gutierrez J, ACM Press, New York, 2004, 155–162.
Feng R Y and Gao X S, A polynomial time algorithm for finding rational general solutions of first order autonomous ODEs, Journal of Symbolic Computation, 2006, 41: 739–762.
Feng R Y, Gao X S, and Huang Z Y, Rational solutions of ordinary difference equations, Journal of Symbolic Computation, 2008, 43: 746–763.
Franz W, The algebro-geometric method for solving algebraic differential equations — A survey, Journal of Systems Science & Complexity, 2019, 32(1): 256–270.
Zhang R F and Bilige S D, Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to p-gBKP equatuon, Nonlinear Dyn., 2019, 95: 3041–3048.
Ma W X, Bilinear equations, Bell polynomials and linear superposition principle, J. Phys. Conf. Ser., 2013, 411: 012021.
Ma W X, Yong X L, and Zhang H Q, Diversity of interaction solutions to the (2+1)-dimensional Ito equation, Comput. Math. Appl., 2018, 75: 289–295.
Lü J Q and Bilige S D, Diversity of interaction solutions to the (3+1)-dimensional Kadomtsev-Petviashvili-Boussinesq-like equation, Mod. Phys. Lett. B, 2018, 32: 1850311.
Lü J Q, Bilige S D, and Gao X Q, Abundant lump solution and interaction phenomenon of (3+1)-dimensional generalized Kadomtsev-Petviashvili equation, Int. J. Nonlinear Sci. Num. Sim., 2019, 20(1): 33–40.
Lü J Q and Bilige S D, The study of lump solution and interaction phenomenon to (2+1)-dimensional Potential Kadomstev-Petviashvili equation, Anal. Math. Phys., 2019, 9(3): 1497–1509.
Lü J Q, Bilige S D, and Chaolu T, The study of lump solution and interaction phenomenon to (2+1)-dimensional generalized fifth-order KdV equation, Nonlinear Dyn., 2018, 91: 1669–1676.
Lü J Q and Bilige S D, Lump solutions of a (2+1)-dimensional bSK equation, Nonlinear Dyn., 2017, 90: 2119–2124.
Zhang R F and Bilige S D, New interaction phenomenon and the periodic lump wave for the Jimbo-Miwa equation, Mod. Phys. Lett. B, 2019, 33: p1950067.
Ma W X, Lump and interaction solutions to linear (4+1)-dimensional PDEs, Acta Mathematica Scientia, 2019, 39B(2): 498–508.
Lü X, Wang J P, Lin F H, et al., Lump dynamics of a generalized two-dimensional Boussinesq equation in shallow water, Nonlinear Dyn., 2018, 91: 1249–1259.
Yin Y H, Ma W X, Liu J G, et al., Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 2018, 76(6): 1275–1283.
Lin F H, Wang J P, Zhou X W, et al., Observation of interaction phenomena for two dimensionally reduced nonlinear models, Nonlinear Dyn., 2018, 94: 2643–2654.
Hua Y F, Guo B L, Ma W X, et al., Interaction behavior associated with a generalized (2+1)-dimensional Hirota bilinear equation for nonlinear waves, Appl. Math. Modell., 2019, 74: 184–198.
Zhang Y, Dong H H, Zhang X E, et al., Rational solutions and lump solutions to the generalized (3+1)-dimensional Shallow Water-like equation, Comput. Math. Appl., 2017, 73: 246–252.
Dong M J, Tian S F, Wang X B, et al., Lump-type solutions and interaction solutions in the (3+1)-dimensional potential Yu-Toda-Sasa-Fukuyama equation, Anal. Math. Phys., 2019, 9: 1511–1523.
Liu J G, Lump-type solutions and interaction solutions for the (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation, Eur. Phys. J. Plus., 2019, 134: 56–61.
Fang T, Gao C N, Wang H, et al., Lump-type solution, rogue wave, fusion and fission phenomena for the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada equation, Modern Physics Letters B, 2019, 33(18): 1950198.
Yue Y F, Huang L L, and Chen Y, Localized waves and interaction solutions to an extended (3+1)-dimensional Jimbo-Miwa equation, Appl. Math. Lett., 2019, 89: 70–77.
Lan Z Z, Rogue wave solutions for a coupled nonlinear Schrödinger equation in the birefringent optical fiber, Appl. Math. Lett., 2019, 98: 128–134.
Zhang X E and Chen Y, General high-order rogue waves to nonlinear Schrödinger-Boussinesq equation with the dynamical analysis, Nonlinear Dyn., 2018, 93: 2169–2184.
Wu X Y, Tian B, Chai H P, et al., Rogue waves and lump solutions for a (3+1)-dimensional generalized B-type Kadomtsev Petviashvili equation in fluid mechanics, Mod. Phys. Lett. B, 2017, 31(22): 1750122.
Lü Z S and Chen Y N, Construction of rogue wave and lump solutions for nonlinear evolution equations, Eur. Phys. J. B., 2015, 88(7): 187–191.
Lü Z S and Chen Y N, Constructing rogue wave prototypes of nonlinear evolution equations via an extended tanh method, Chaos, Solitons Fractals, 2015, 81: 218–223.
Liu J G, Lump-type solutions and interaction solutions for the (2+1)-dimensional generalized fifth-order KdV equation, Appl. Math. Lett., 2018, 86: 36–41.
Wazwaz A M, Liu W, and Zhang X X, High-order breathers, lumps, and semirational solutions to the (2+1)-dimensional Hirota-Satsuma-Ito equation, Phys. Scr., 2019, 94: 075203.
Zhang R F, Bilige S D, Fang T, et al., New periodic wave, cross-kink wave and the interaction phenomenon for the Jimbo-Miwa-like equation, Comput. Math. Appl., 2019, 78: 754–764.
Ma W X, Qin Z Y, and Lü X, Lump solutions to dimensionally reduced p-gKP and p-gBKP equations, Nonlinear Dyn., 2016, 84: 923–931.
Zhang R F, Bilige S D, Bai Y X, et al., Interaction phenomenon to dimensionally reduced p-gBKP equation, Mod. Phys. Lett. B, 2018, 32: 1850074.
Kaur L and Wazwaz A M, Lump, breather and solitary wave solutions to new reduced form of the generalized BKP equation, International Journal of Numerical Methods for Heat and Fluid Flow, 2019, 29(2): 569–579.
Ma W X, Generalized bilinear differential equations, Studies in Nonlinear Sciences, 2011, 2(4): 140–144.
Zhao Z L, Chen Y, and Han B, Lump soliton, mixed lump stripe and periodic lump solutions of a (2+1)-dimensional asymmetrical Nizhnik-Novikov-Veselov equation, Mod. Phys. Lett. B, 2017, 31: 1750157.
Hu C C, Tian B, Yin H M, et al., Dark breather waves, dark lump waves and lump wave-soliton interactions for a (3+1)-dimensional generalized Kadomtsev-Petviashvili equation in a fluid, Comput. Math. Appl., 2019, 78: 166–177.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the National Natural Science Foundation of China under Grant Nos. 11661060, 11571008, the Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region under Grant No. NJYT-20-A06 and the Natural Science Foundation of Inner Mongolia Autonomous Region of China under Grant No. 2018LH01013.
This paper was recommended for publication by Editor-in-Chief GAO Xiao-Shan.
Rights and permissions
About this article
Cite this article
Zhang, R., Bilige, S. & Chaolu, T. Fractal Solitons, Arbitrary Function Solutions, Exact Periodic Wave and Breathers for a Nonlinear Partial Differential Equation by Using Bilinear Neural Network Method. J Syst Sci Complex 34, 122–139 (2021). https://doi.org/10.1007/s11424-020-9392-5
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-020-9392-5