Skip to main content
Springer Nature Link
Log in

The Complex Dynamics of Hepatitis B Infected Individuals with Optimal Control

  • Published:
Journal of Systems Science and Complexity Aims and scope Submit manuscript

Abstract

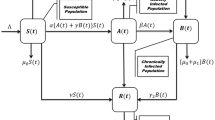
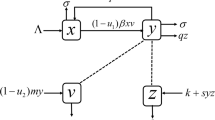
This paper proposes various stages of the hepatitis B virus (HBV) besides its transmissibility and nonlinear incidence rate to develop an epidemic model. The authors plan the model, and then prove some basic results for the well-posedness in term of boundedness and positivity. Moreover, the authors find the threshold parameter R0, called the basic/effective reproductive number and carry out local sensitive analysis. Furthermore, the authors examine stability and hence condition for stability in terms of R0. By using sensitivity analysis, the authors formulate a control problem in order to eradicate HBV from the population and proved that the control problem actually exists. The complete characterization of the optimum system was achieved by using the 4th-order Runge-Kutta procedure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zou L, Ruan S, and Zhang W, On the sexual transmission dynamics of hepatitis B virus in China, Journal of Theoretical Biology, 2015, 369: 1–12.

    Article  MathSciNet  Google Scholar 

  2. Haq F, Shah K, Khan A, et al., Numerical solution of fractional order epidemic model of a vector born disease by Laplace Adomian decomposition method, Punjab University Journal of Mathematics, 2017, 49(2): 13–22.

    MathSciNet  MATH  Google Scholar 

  3. Haq F, Shah A, Rahman G U, et al., Numerical solution of fractional order smoking model via Laplace Adomian decomposition method, Alexandria Engineering Journal, 2018, 57(2): 1061–1069.

    Article  Google Scholar 

  4. Pang L, Ruan S, Liu S, et al., Transmission dynamics and optimal control of measles epidemics, Applied Mathematics and Computation, 2015, 256: 131–147.

    Article  MathSciNet  Google Scholar 

  5. Khan A and Zaman G, Asymptotic behavior of an age structure SIRS endemic model, Applied and Computational Mathematics, 2018, 17(2): 185–204.

    MathSciNet  MATH  Google Scholar 

  6. Zaman G, Kang Y H, and Jung I H, Stability analysis and optimal vaccination of an SIR epidemic model, BioSystems, 2008, 93: 240–249.

    Article  Google Scholar 

  7. Zeb A, Zaman G, and Momani S, Square-root dynamics of a giving up smoking model, Applied Mathematical Modelling, 2013, 37: 5326–5334.

    Article  MathSciNet  Google Scholar 

  8. Rahman G U, Shah K, Haq F, et al., Host vector dynamics of pine wilt disease model with convex incidence rate, Chaos, Solitons & Fractals, 2018, 113: 31–39.

    Article  MathSciNet  Google Scholar 

  9. Zaman G, Kang Y H, and Jung I H, Optimal treatment of an SIR epidemic model with time delay, BioSystems, 2009, 98: 43–50.

    Article  Google Scholar 

  10. Khan T and Zaman G, Classification of different Hepatitis B infected individuals with saturated incidence rate, SpringerPlus, 2016, 5: 1082.

    Article  Google Scholar 

  11. Khan A and Zaman G, Optimal control strategy of SEIR endemic model with continuous age-structure in the exposed and infectious classes, Optimal Control Applications and Methods, 2018, 39: 1716–1727.

    Article  MathSciNet  Google Scholar 

  12. Abdo M S, Shah K, Wahash H A, et al., On a comprehensive model of the novel coronavirus (COVID-19) under Mittag-Leffler derivative, Chaos, Solitons & Fractals, 2020, 135: 1–14.

    Article  MathSciNet  Google Scholar 

  13. World Health Organization, Hepatitis b fact sheet, no 204 [updated July 2015], World Health Organization, Geneva, Switzerland, 2013.

    Google Scholar 

  14. Anwarud D, Li Y J, and Liu Q, Viral dynamics and control of hepatitis B virus (HBV) using an epidemic model, Alexandria Engineering Journal, 2020, 59(2): 667–679.

    Article  Google Scholar 

  15. Thornley S, Bullen C, and Roberts M, Hepatitis B in a high prevalence New Zealand population: A mathematical model applied to infection control policy, Journal of Theoretical Biology, 2008, 254: 599–603.

    Article  MathSciNet  Google Scholar 

  16. Khan T, Zaman G, and Saleh Alshomrani A, Spreading dynamic of acute and carrier hepatitis B with nonlinear incidence, PLoS ONE, 2018, 13: e0191914.

    Article  Google Scholar 

  17. Shah K, Jarad F, and Abdeljawad T, On a nonlinear fractional order model of dengue fever disease under Caputo-Fabrizio derivative, Alexandria Engineering Journal, 2020, 59: 2305–2313.

    Article  Google Scholar 

  18. Fan M, Li M Y, and Wang K, Global stability of an SEIS epidemic model with recruitment and a varying total population size, Mathematical Biosciences, 2001, 170: 199–208.

    Article  MathSciNet  Google Scholar 

  19. Li J and Ma Z, Qualitative analyses of SIS epidemic model with vaccination and varying total population size, Mathematical and Computer Modelling, 2002, 35: 1235–1243.

    Article  MathSciNet  Google Scholar 

  20. Lashari A A, Hattaf K, Zaman G, et al., Backward bifurcation and optimal control of a vector borne disease, Applied Mathematics and Information Sciences, 2013, 7: 301–309.

    Article  MathSciNet  Google Scholar 

  21. Zou L, Zhang W, and Ruan S, Modeling the transmission dynamics and control of hepatitis B virus in China, Journal of Theoretical Biology, 2010, 262: 330–338.

    Article  MathSciNet  Google Scholar 

  22. Van den Driessche P and Watmough J, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Mathematical Biosciences, 2002, 180: 29–48.

    Article  MathSciNet  Google Scholar 

  23. Van Den Driessche P and Watmough J, Mathematical Epidemiology, Springer Verlag, New York, 2008.

    Google Scholar 

  24. Koonprasert S, Moore E J, and Banyatlersthaworn S, Sensitivity and stability analysis of hepatitis B virus model with non-cytolytic cure process and logistic hepatocyte growth, Global Journal of Pure and Applied Mathematics, 2016, 12(3): 2297–2312.

    Google Scholar 

  25. Momoh A A, Ibrahim M O, Madu B A, et al., Global equilibrium stability of hepatitis B model and vaccination impact, Research Journal of Mathematics and Statistics, 2012, 4(3): 57–62.

    Google Scholar 

  26. Cheng Y, Qiuhui P, and He M, Stability analysis of hepatitis B virus model with incomplete immunization of HepB vaccine, Abstract and Applied Analysis, 2014, 1–11.

  27. Cao J, Wang Y, Alofi A, et al., Global stability of an epidemic model with carrier state in heterogeneous networks, IMA Journal of Applied Mathematics, 2015, 80(4): 1025–1048.

    Article  MathSciNet  Google Scholar 

  28. Kamien M I and Schwartz N L, Dynamic Optimization: The Calculus of Variations and Optimal Control in Economics and Management, North Holland, Inc, 1998.

  29. Culshaw R V, Ruan S, and Spiteri R J, Optimal HIV treatment by maximising immune response, Journal of Mathematical Biology, 2004, 48: 545–562.

    Article  MathSciNet  Google Scholar 

  30. Kirschner D, Lenhart S, and Serbin S, Optimal control of the chemotherapy of HIV, Journal of Mathematical Biology, 1997, 35: 775–792.

    Article  MathSciNet  Google Scholar 

  31. Suzanne L and Workman J T, Optimal Control Applied to Biological Models, Chapman and Hall/CRC, 2007.

  32. Khan T, Zaman G, and Chohan M I, The transmission dynamic and optimal control of acute and chronic hepatitis B, Journal of Biological Dynamics, 2017, 11: 172–189.

    Article  MathSciNet  Google Scholar 

  33. Zhang J and Zhang S, Application and optimal control for an HBV model with vaccination and treatment, Discrete Dynamics in Nature and Society, 2018, Article ID 2076983, 13 pages.

  34. Kamyad A, Akbari R, Heydari A, et al., Mathematical modeling of transmission dynamics and optimal control of vaccination and treatment for hepatitis B virus, Computational and Mathematical Methods in Medicine, 2014, Article ID 475451, 15 pages.

  35. Goyal A, Murray J M, Roadmap to control HBV and HDV epidemics in China, Journal of Theoretical Biology, 2017, 423: 41–52.

    Article  Google Scholar 

  36. Pontryagin L, The Mathematical Theory of Optimal Processed, Taylor and Francis, London, UK, 1987.

    Google Scholar 

  37. Nana-Kyere S, Ackora-Prah J, Okyere E, et al., Hepatitis B optimal control model with vertical transmission, Appl. Math., 2017, 7(1): 5–13.

    Google Scholar 

  38. Ijalana C O and Yusuf T T, Optimal control strategy for hepatitis B virus epidemic in areas of high endemicity, International Journal of Scientific and Innovative Mathematical Research, 2017, 5(12): 28–39.

    Google Scholar 

  39. Birkhoff G and Rota G, Ordinary Differential Equations, 4th Edition, John Wiley and Sons, New York, NY, USA, 1989.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Sun Yat-sen University, Guangzhou, 510275, China

    Anwarud Din & Yongjin Li

  2. School of Mathematical Sciences, Beijing Normal University, Beijing, 100875, China

    Murad Ali Shah

Authors
  1. Anwarud Din
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yongjin Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Murad Ali Shah
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yongjin Li.

Additional information

This research was supported by the National Natural Science Foundation of China under Grant No. 11971493.

This paper was recommended for publication by Editor YOU Keyou.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Din, A., Li, Y. & Shah, M.A. The Complex Dynamics of Hepatitis B Infected Individuals with Optimal Control. J Syst Sci Complex 34, 1301–1323 (2021). https://doi.org/10.1007/s11424-021-0053-0

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11424-021-0053-0

Keywords