Abstract
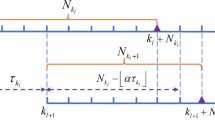
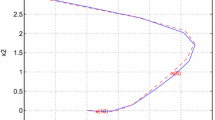
In this paper, an approximation-based event-triggered model predictive control (AETMPC) strategy is proposed to implement event-triggered model predictive control for continuous-time constrained nonlinear systems under the digital platform. In the AETMPC strategy, both of the optimal control problem (OCP) and the triggering conditions are defined in a discrete-time manner based on approximate discrete-time models, while the plant under control is continuous time. In doing so, sensing load is alleviated because the triggering condition does not need to be checked continuously, and the computation of the OCP is simpler since which is calculated in the discrete-time framework. Meanwhile, robust constraints are satisfied in a continuous-time sense by taking inter-sampling behavior into consideration, and a novel constraint tightening approach is presented accordingly. Furthermore, the feasibility of the AETMPC strategy is analyzed and the associated stability of the overall system is established. Finally, this strategy is validated by a numerical example.
Similar content being viewed by others
References
Zhao Y B, Liu G P, Kang Y, et al., Packet-Based Control for Networked Control Systems, University of Glamorgan, Pontypridd, 2008.
Liu C, Gao J, Li H, et al., Aperiodic robust model predictive control for constrained continuous-time nonlinear systems: An event-triggered approach, IEEE Transactions on Cybernetics, 2017, 48(5): 1397–1405.
Li H and Shi Y, Event-triggered robust model predictive control of continuous-time nonlinear systems, Automatica, 2014, 50(5): 1507–1513.
Hashimoto K, Adachi S, and Dimarogonas D V, Event-triggered intermittent sampling for nonlinear model predictive control, Automatica, 2017, 81: 148–155.
Eqtami A, Dimarogonas D V, and Kyriakopoulos K J, Event-triggered control for discrete-time systems, IEEE Proceedings of the 2010 American Control Conference, 2010, 4719–4724.
Sun Z, Dai L, Liu K, et al., Robust self-triggered MPC with adaptive prediction horizon for perturbed nonlinear systems, IEEE Transactions on Automatic Control, 2019, 64(11): 4780–4787.
Wang M, Sun J, and Chen J, Input-to-state stability of perturbed nonlinear systems with event-triggered receding horizon control scheme, IEEE Transactions on Industrial Electronics, 2018, 66(8): 6393–6403.
Li P, Kang Y, Zhao Y B, et al., Networked dual-mode adaptive horizon MPC for constrained nonlinear systems, IEEE Transactions on Systems, Man, and Cybernetics: Systems, early access, DOI: https://doi.org/10.1109/TSMC.2020.2971241.
Magni L and Scattolini R, Model predictive control of continuous-time nonlinear systems with piecewise constant control, IEEE Transactions on Automatic Control, 2004, 49(6): 900–906.
Sopasakis P, Patrinos P, and Sarimveis H, MPC for sampled-data linear systems: Guaranteeing constraint satisfaction in continuous-time, IEEE Transactions on Automatic Control, 2013, 59(4): 1088–1093.
Nei D, Teel A R, and Kokotovi P V, Sufficient conditions for stabilization of sampled-data nonlinear systems via discrete-time approximations, Systems & Control Letters, 1999, 38(4–5): 259–270.
He N and Shi D, Event-based robust sampled-data model predictive control: A non-monotonic Lyapunov function approach, IEEE Transactions on Circuits and Systems I: Regular Papers, 2015, 62(10): 2555–2564.
Khalil H K and Grizzle J W, Nonlinear Systems, Upper Saddle River, NJ: Prentice hall, 2002.
Rubagotti M, Raimondo D M, Ferrara A, et al., Robust model predictive control with integral sliding mode in continuous-time sampled-data nonlinear systems, IEEE Transactions on Automatic Control, 2010, 56(3): 556–570.
Jiang Z P and Praly L, Design of robust adaptive controllers for nonlinear systems with dynamic uncertainties, Automatica, 1998, 34(7): 825–840.
Grne L and Nesic D, Optimization-based stabilization of sampled-data nonlinear systems via their approximate discrete-time models, SIAM Journal on Control and Optimization, 2003, 42(1): 98–122.
Chen H and Allgwer F, A quasi-infinite horizon nonlinear model predictive control scheme with guaranteed stability, Automatica, 1998, 34(10): 1205–1217.
Rajhans C, Patwardhan S C, and Pillai H, Discrete time formulation of quasi infinite horizon nonlinear model predictive control scheme with guaranteed stability, IFAC-Papers OnLine, 2017, 50(1): 7181–7186.
Grne L and Pannek J, Nonlinear model predictive control, Nonlinear Model Predictive Control, Springer, Cham, 2017, 45–69.
Nei D, Teel A R, and Sontag E D, Formulas relating KL stability estimates of discrete-time and sampled-data nonlinear systems, Systems & Control Letters, 1999, 38(1): 49–60.
Limn D, Alamo T, Salas F, et al., Input to state stability of minmax MPC controllers for nonlinear systems with bounded uncertainties, Automatica, 2006, 42(5): 797–803.
Stuart A and Humphries A R, Dynamical Systems and Numerical Analysis, Cambridge University Press, Cambridge, 1998.
Wang T, Kang Y, Li P, et al., Robust model predictive control for constrained networked nonlinear systems: An approximation-based approach, Neurocomputing, 418: 56–65.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper was supported by the National Key Research and Development Program of China under Grant Nos. 20I8AAA0I00800 and 20I8YFE0I06800, the National Natural Science Foundation of China under Grant Nos. 61725304, 6I67336I, 61673350 and 61422307, the Science and Technology Major Project of Anhui Province under Grant No. 9I2I98698036, the Chinese Academy of Sciences, the Youth Top-notch Talent Support Program and the Youth Yangtze River Scholar, and the Project funded by China Postdoctoral Science Foundation under Grand No. 2020M682036.
This paper was recommended for publication by Editor GUO Jin.
Rights and permissions
About this article
Cite this article
Wang, T., Kang, Y., Li, P. et al. Robust Approximation-Based Event-Triggered MPC for Constrained Sampled-Data Systems. J Syst Sci Complex 34, 2109–2124 (2021). https://doi.org/10.1007/s11424-021-0073-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-021-0073-9