Abstract
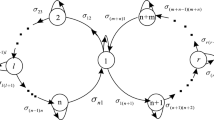
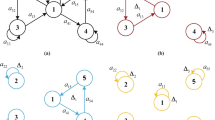
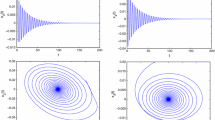
Up till the present moment, researchers have always featured the single-ring neural network. These investigations, however, disregard the link between rings in neural networks. This paper highlights a high-dimensional double-ring neural network model with multiple time delays. The neural network has two rings of a shared node, where one ring has n neurons and the other has m + 1 neurons. By utilizing the sum of time delays as the bifurcation parameter, the method of Coates’ flow graph is applied to obtain the relevant characteristic equation. The stability of the neural network model with bicyclic structure is discussed by dissecting the characteristic equation, and the critical value of Hopf bifurcation is derived. The effect of the sum of time delays and the number of neurons on the stability of the model is extrapolated. The validity of the theory can be verified by numerical simulations.
Similar content being viewed by others
References
Lian D, Existence and global exponential stability of pseudo almost periodic solutions of a general delayed BAM neural networks, Journal of Systems Science and Complexity, 2018, 31(3): 608–620.
Mai V T and Dinh C H, Robust finite-time stability and stabilization of a class of fractional-order switched nonlinear systems, Journal of Systems Science and Complexity, 2019, 32(6): 1479–1497.
Ralph E H, Donald M Q, Carolyn M M, et al., Cortical instability and the mechanism of mania: A neural network simulation and perceptual test, Biol. Psychiatry, 2001, 49(6): 500–509.
Jefferson M F, Pendleton N, Lucas C P, et al., Evolution of artificial neural network architecture Prediction of depression after mania, Methods Inf. Med., 1998, 37(3): 220–225.
Zieglgansberger W and Tolle T R, The pharmacology of pain signalling, Curr. Opin. Neurobiol., 1993, 3(4): 611–618.
Hopfield J J, Neurons with graded response have collective computational properties like those of two-state neurons, Proc. Natl. Acad. Sci. U. S. A., 1984, 81(10): 3088–3092.
Duan L, Shi M, and Huang L H, New results on finite-/fixed-time synchronization of delayed diffusive fuzzy HNNs with discontinuous activations, Fuzzy Sets Syst., 2020, https://doi.org/10.1016/j.fss.2020.04.016.
Luo S H, Li S B, and Tajaddodianfar F, Chaos and nonlinear feedback control of the arch micro-electro-mechanical system, Journal of Systems Science and Complexity, 2018, 31(6): 1510–1524.
Zhang R, Ding G Y, Zhang F Q, et al., The application of intelligent algorithm and pulse coupled neural network in medical image process, J. Med. Imaging Health Inform., 2017, 7(4): 775–779.
Secco J, Poggio M, and Corinto F, Supervised neural networks with memristor binary synapses, Int. J. Circuit Theory Appl., 2018, 46(1): 221–233.
Song Y D, Lewis F L, and Polycarpou M, Guest editorial special issue on new developments in neural network structures for signal processing, autonomous decision, and adaptive control, IEEE Trans. Neural Netw. Learn. Syst., 2017, 28(3): 494–499.
Zhang P, Li C, and Huang T, Forgetting memristor based neuromorphic system for pattern training and recognition, Neurocomputing, 2017, 222(222): 47–53.
Huang C D, Nie X B, Zhao X, et al., Novel bifurcation results for a delayed fractional-order quaternion-valued neural network, Neural Netw., 2019, 117: 67–93.
Kais B, A new class of neural networks and its applications, Neurocomputing, 2017, 249: 28–47.
Xue H B and Zhang J Y, Robust exponential stability of switched interval interconnected systems with unbounded delay, Journal of Systems Science and Complexity, 2017, 30(6): 1316–1331.
Ge J H and Xu J, Stability and Hopf bifurcation on four-neuron neural networks with inertia and multiple delays, Neurocomputing, 2018, 287: 34–44.
Duan L, Huang L H, Guo Z Y, et al., Periodic attractor for reaction-diffusion high-order Hopfield neural networks with time-varying delays, Comput. Math. with Appl., 2016, 73(2): 233–245.
Duan L, Wei H, and Huang L H, Finite-time synchronization of delayed fuzzy cellular neural networks with discontinuous activations, Fuzzy Sets Syst., 2018, 361: 56–70.
Mao X C and Wang Z H, Stability, bifurcation, and synchronization of delay-coupled ring neural networks, Nonlinear Dyn., 2016, 84(2): 1063–1078.
Liu B, Hill D J, Zhang C F, et al., Stabilization of discrete-time dynamical systems under event-triggered impulsive control with and without time-delays, Journal of Systems Science and Complexity, 2018, 31(1): 130–146.
Jiang D P and Zhang K Z, Observability of boolean control networks with time-variant delays in states, Journal of Systems Science and Complexity, 2018, 31(2): 436–445.
Zhang Q J, Wu X Q, and Liu J, Pinning synchronization of discrete-time complex networks with different time-varying delays, Journal of Systems Science and Complexity, 2019, 32(6): 1560–1571.
Masaki K, Multistate vector product hopfield neural networks, Neurocomputing, 2018, 272: 425–431.
Reza M S and Saeed F, On a discrete-time-delayed Hopfield neural network with ring structures and different internal decays: Bifurcations analysis and chaotic behavior, Neurocomputing, 2015, 151: 188–195.
Collins J J and Stewart I, A group-theoretic approach to rings of coupled biological oscillators, Biol. Cybern., 1994, 71(2): 95–103.
Zhang C R, Sui Z Z, and Li H P, Equivariant bifurcation in a coupled complex-valued neural network rings, Chaos Solitons Fractals, 2017, 98: 22–30.
Bi P and Hu Z X, Hopf bifurcation and stability for a neural network model with mixed delays, Appl. Math. Comput., 2012, 218(12): 6748–6761.
Hu H J and Huang L H, Stability and Hopf bifurcation analysis on a ring of four neurons with delays, Appl. Math. Comput., 2009, 213(2): 587–599.
Xu C J and Zhang Q M, Anti-periodic solutions in a ring of four neurons with multiple delays, Int. J. Comput. Math., 2015, 92(5): 1086–1100.
Cai T Y, Zhang H G, and Yang F S, Simplified frequency method for stability and bifurcation of delayed neural networks in ring structure, Neurocomputing, 2013, 121: 416–422.
Huang C D, Cao J D, Xiao M, et al., Effects of time delays on stability and Hopf bifurcation in a fractional ring-structured network with arbitrary neurons, Commun. Nonlinear Sci. Numer. Simul., 2018, 57: 1–13.
Desoer C A, The optimum formula for the gain of a flow graph or a simple derivation of Coates’ formula, Proceedings of the IRE, 1960, 48: 883–889.
Cheng Z S, Xie K H, Wang T S, et al., Stability and Hopf bifurcation of three-triangle neural networks with delays, Neurocomputing, 2018, 322: 206–215.
Li L, Wang Z, Li Y X, et al., Hopf bifurcation analysis of a complex-valued neural network model with discrete and distributed delays, Appl. Math. Comput., 2018, 330: 152–169.
Wang T S, Cheng Z S, Bu R, et al., Stability and Hopf bifurcation analysis of a simplified six-neuron tridiagonal two-layer neural network model with delays, Neurocomputing, 2019, 332: 203–214.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the National Natural Science Foundation of China under Grant Nos. 61573194, 62073172, 61877033, and the Natural Science Foundation of Jiangsu Province of China under Grant No. BK20181389.
This paper was recommended for publication by Editor XIN Bin.
Rights and permissions
About this article
Cite this article
Xing, R., Xiao, M., Zhang, Y. et al. Stability and Hopf Bifurcation Analysis of an (n + m)-Neuron Double-Ring Neural Network Model with Multiple Time Delays. J Syst Sci Complex 35, 159–178 (2022). https://doi.org/10.1007/s11424-021-0108-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-021-0108-2