Abstract
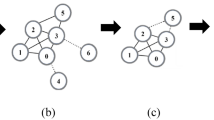
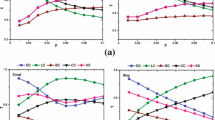
The study on how to identify influential spreaders in complex networks is becoming increasingly significant. Previous studies demonstrate that considering the shortest path length can improve the accuracy of identification, but which ignore the influence of the number of shortest paths. In many cases, even though the shortest path length of two nodes is rather larger, their interaction influence is also significant if the number of shortest paths between them is considerable. Inspired by this fact, the authors propose an improved centrality index (ICC) based on well-known closeness centrality and a semi-local iterative algorithm (semi-IA) to study the impact of the number of shortest paths on the identification of the influential spreaders. By comparing with several traditional centrality indices, such as degree centrality, k-shell decomposition, betweenness centrality and eigenvector centrality, the experimental results on real networks indicate that the ICC index and semi-IA have a better performance, regardless of the identification capability or the resolution.
Similar content being viewed by others
References
Basaras P, Katsaros D, and Tassiulas L, Detecting influential spreaders in complex, dynamic networks, Computer, 2013, 46(4): 24–29.
Lü L, Zhang Y C, Yeung C H, et al., Leaders in social networks, the delicious case, PLoS One, 2011, 6(6): e21202.
Borge-Holthoefer J and Moreno Y, Absence of influential spreaders in rumor dynamics, Physical Review E, 2012, 85(2): 026116.
Wang P, Tian C, and Lu J, Identifying influential spreaders in artificial complex networks, Journal of Systems Science and Complexity, 2014, 27(4): 650–665.
Chen D B, Xiao R, Zeng A, et al., Path diversity improves the identification of influential spreaders, EPL (Europhysics Letters), 2013, 104(6): 68006.
Ren Z M, Zeng A, Chen D B, et al., Iterative resource allocation for ranking spreaders in complex networks, EPL (Europhysics Letters), 2014, 106(4): 48805.
Ahmad Z and Amir S, A hierarchical approach for influential node ranking in complex social networks, Expert Systems with Applications, 2018, 93: 200–211.
Sotoodeh H and Falahrad M, Relative degree structural hole centrality, CRD-SH: A new centrality measure in complex networks, Journal of Systems Science and Complexity, 2019, 32(5): 1306–1323.
Tang J, Zhang R, Wang P, et al., A discrete shuffled frog-leaping algorithm to identify influential nodes for influence maximization in social networks, Knowledge-Based Systems, 2020, 187: 104833.
Bonacich P, Factoring and weighting approaches to status scores and clique identification, Journal of Mathematical Sociology, 1972, 2(1): 113–120.
Kitsak M, Gallos L K, Havlin S, et al. A, Identification of influential spreaders in complex networks, Nature Physics, 2010, 6(11): 888–893.
Freeman L C, A set of measures of centrality based on betweenness, Sociometry, 1977, 40(1): 35–41.
Bonacich P, Power and centrality: A family of measures, Journal of Mathematical Sociology, 1987, 92(1): 1170–1182.
Zeng A and Zhang C J, Ranking spreaders by decomposing complex networks, Physics Letters A, 2013, 377(14): 1031–1035.
Sabidussi G, The centrality index of a graph, Psychometrika, 1966, 31(4): 581–603.
Ma L L, Ma C, Zhang H F, et al., Identifying influential spreaders in complex networks based on gravity formula, Physica A, 2016, 451: 205–212.
Liu H L, Ma C, Xiang B B, et al., Identifying multiple influential spreaders based on generalized closeness centrality, Physica A, 2018, 492(1): 2237–2248.
Bao Z K, Ma C, Xiang B B, et al., Identification of influential nodes in complex networks: Method from spreading probability viewpoint, Physica A, 2017, 468: 391–397.
Benzi M, Estrada E, and Klymko C, Ranking hubs and authorities using matrix functions, Linear Algebra and Its Applications, 2013, 438(5): 2447–2474.
Liu Y, Tang M, Zhou T, et al., Core-like groups result in invalidation of identifying superspreader by k-shell decomposition, Scientific Reports, 2015, 5: 9602.
Newman M E, Finding community structure in networks using the eigenvectors of matrices, Physical Review E, 2006, 74(3): 036104.
Watts D J and Strogatz S H, Collective dynamics of small-worldnetworks, Nature, 1998, 393(6684): 440–442.
Guimera R, Danon L, Diaz-Guilera A, et al., Self-similar community structure in a network of human interactions, Physical Review E, 2003, 68(6): 065103.
Blagus N, Subelj L, Bajec M, Self-similar scaling of density in complex real-world networks, Physica A, 2012, 391(8): 2794–2802.
Duch J and Arenas A, Community detection in complex networks using extremal optimization, Physical Review E, 2005, 72: 027104.
Mering C V, Krause R, Snel B, et al., Comparative assessment of large-scale data sets of proteinprotein interactions, Nature, 2002, 417: 399–403.
Spring N, Mahajan R, Wetherall D, et al., Measuring ISP topologies with rocketfuel, IEEE/ACM Transactions on Networking, 2004, 12(1): 2–16.
Leskovec J, Kleinberg J, and Faloutsos C, Graph evolution: Densification and shrinking diameters, ACM Transactions on Knowledge Discovery from Data (TKDD), 2007, 1(1): 2–42.
Moreno Y, Pastor-Satorras R, and Vespignani A, Epidemic outbreaks in complex heterogeneous networks, The European Physical Journal B, 2002, 26(4): 521–529.
Bae J and Kim S, Identifying and ranking influential spreaders in complex networks by neighborhood coreness, Physica A, 2014, 395: 549–559.
Knight W R, A computer method for calculating kendall’s tau with ungrouped data, Journal of the American Statistical Association, 1966, 61(314): 436–439.
Zhou T, Lü L, and Zhang Y C, Predicting missing links via local information, The European Physical Journal B, 2009, 71(4): 623–630.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the National Natural Science Foundation of China under Grant Nos. 61973001, 61806001, the Natural Science Foundation of Anhui Province under Grant No. 1808085MF201, the State Key Laboratory for Ocean Big Data Mining and Application of Zhejiang Province under Grant No. OBDMA201502, and Anhui University Foundation under Grant No. 01005102.
This paper was recommended for publication by Editor LIU Guoping.
Rights and permissions
About this article
Cite this article
Luan, Y., Bao, Z. & Zhang, H. Identifying Influential Spreaders in Complex Networks by Considering the Impact of the Number of Shortest Paths. J Syst Sci Complex 34, 2168–2181 (2021). https://doi.org/10.1007/s11424-021-0111-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-021-0111-7