Abstract
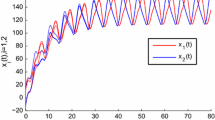
This paper investigates the exponential stability of traveling wave solutions for nonlinear delayed cellular neural networks. As a continuity of the past work (Wu and Niu, 2016; Yu, et al., 2011) on the existence and uniqueness of the traveling wave solutions, it is very reasonable and interesting to consider the exponential stability of the traveling wave solutions. By the weighted energy method, comparison principle and the first integral mean value theorem, this paper proves that, for all monotone traveling waves with the wave speed \(c < c_1^ \ast < 0\) or \(c > c_2^ \ast > 0\), the solutions converge time-exponentially to the corresponding traveling waves, when the initial perturbations decay at some fields.
Similar content being viewed by others
References
Chua L and Yang L, Cellular neural networks: Theory, IEEE Trans. Circuits Syst., 1988, 35: 1257–1272.
Chua L and Yang L, Cellular neural networks: Applications, IEEE Trans. Circuits Syst., 1988, 35: 1273–1290.
Liu D Y, Zhang J H, Guan X P, et al., Global asymptotic stability of cellular neural networks with delay, Appl. Math. Mech. — Engl. Ed., 2008, 29(6): 811–816.
Ban J C and Chang C H, Realization problem of multi-layer cellular neural networks, Neural Networks, 2015, 70: 9–17.
Zhang X J, Wang G X, and Liu H, Stability analysis of delayed cellular neural networks with and without noise perturbation, Appl. Math. Mech. — Engl. Ed., 2008, 29(11): 1427–1438.
Wu S L and Niu T C, Qualitative properties of traveling waves for nonlinear cellular neural networks with distributed delays, Journal of Mathematical Analysis and Applications, 2016, 434(1): 617–632.
Cao J, On exponential stability and periodic solutions of CNNs with delays, Phys. Lett. A, 2000, 267: 312–318.
Guo Y and Liu S T, Global exponential stability analysis for a class of neural networks with time delays, International Journal of Robust and Nonlinear Control, 2012, 22: 1484–1494.
Yu Z, Yuan R, Hsu C H, et al., Traveling waves for nonlinear cellular neural networks with distributed delays, Journal of Differential Equations, 2011, 251(3): 630–650.
Guo Y and Cao J, Stability and stabilization for stochastic Cohen-Grossberg neural networks with impulse control and noise-induced control, Int J Robust Nonlinear Control, 2019, 29: 153–165.
Chérif F, Existence and global exponential stability of pseudo almost periodic solution for SICNNs with mixed delays, J. Appl. Math. Comput., 2012, 39: 235–251.
N’Guérékata G M, Almost Automorphic and Almost Periodic Functions in Abstract Spaces, Kluwer Academic Publishers, New York, 2001.
Yang Y and Liu L, Stability of traveling waves in a population dynamics model with spatiotemporal delay, Nonlinear Analysis, 2016, 132: 183–195.
Mei M, So J W, Li M, et al., Asymptotic stability of travelling waves for Nicholson’s blowflies equation with diffusion, Proc. Royal Soc. Edinburgh Sect. A, 2004, 134: 579–594.
Yu Z X and Mei M, Uniqueness and stability of traveling waves for cellular neural networks with multiple delays, J. Differential Equations, 2016, 260: 241–267.
Lin C K and Mei M, On traveling wavefronts of Nicholson’s blowflies equations with diffusion, Proc. Roy. Soc. Edinburgh Sect. A, 2010, 140: 135–152.
Guo Y, Globally robust stability analysis for stochastic Cohen-Grossberg neural networks with impulse and time-varying delays, Ukrainian Mathematical Journal, 2018, 69(8): 1049–1060.
Guo Y, Exponential stability analysis of traveling waves solutions for nonlinear delayed cellular neural networks, Dynamical Systems — An International Journal, 2017, 32(4): 490–503.
Guo Y and Xin L, Asymptotic and robust mean square stability analysis of impulsive high-order BAM neural networks with time-varying delays, Circuits, Systems, and Signal Processing, 2018, 37(7): 2805–2823.
Wang N, Li X C, Lu J Q, et al., Unified synchronization criteriain an array of coupled neural networks with hybrid impulses, Neural Networks, 2018, 101: 25–32.
Yu Z X and Mei M, Uniqueness and stability of traveling waves for cellular neural networks with multiple delays, J. Differential Equations, 2018, 260: 241–267.
Zhu Q, Cao J, Hayat T, et al., Robust stability of Markovian jump stochastic neural networks with time delays in the leakage terms, Neural Process. Lett., 2015, 41(1): 1–27.
Jiang H and Teng T, Global exponential stability of cellular neural networks with time-varying coefficients and delays, Neural Networks, 2004, 17: 1415–1425.
Arik S, An analysis of global asymptotic stability of delayed cellular neural networks, IEEE Trans. Neural Networks, 2002, 13: 1239–1242.
Li T, Fei S, and Zhu Q, Design of exponential state estimator for neural networks with distributed delays, Nonlinear Analysis: Real World Applications, 2009, 10: 1229–1242.
Bouzerdoum A and Pinter R B, Analysis and analog implementation of directionally sensitive shunting inhibitory cellular neural networks, Visual Information Processing: From Neurons to Chips, in: SPIE, 1991, 1473: 29–38.
Bouzerdoum A and Pinter R B, Nonlinear lateral inhibition applied to motion detection in the fly visual system, Eds. by Pinter R B and Nabet B, Nonlinear Vision, CRC Press, Boca Raton, FL, 1992, 423–450.
Mohamad S, Global exponential stability in continuous-time and discrete-time delay bidirectional neural networks, Physica D, 2001, 159: 233–251.
Forti M and Tesi A, New conditions for global stability of neural network with application to linear and quadratic programming problems, IEEE Trans. Circ. Syst. I: Fundam. Theory Appl., 1995, 42: 354–366.
Morita M, Associative memory with non-monotone dynamics, Neural Networks, 1993, 6: 115–126.
Yoshizawa S, Morita M, and Amari S, Capacity of associative memory using a non-monotonic neuron networks, Neural Networks, 1993, 6: 167–176.
Guo Y, Global asymptotic stability analysis for integro-differential systems modeling neural networks with delays, Z. Angew. Math. Phys., 2010, 61: 971–978.
Rathinasamy A and Narayanasamy J, Mean square stability and almost sure exponential stability of two step Maruyama methods of stochastic delay Hopfield neural networks, Applied Mathematics and Computation, 2019, 348: 126–152.
Syed A M, Yogambigai J, Saravanan S, et al., Stochastic stability of neutral-type Markovian-jumping BAM neural networks with time varying delays, Journal of Computational and Applied Mathematics, 2019, 349: 142–156.
Arbi A, Dynamics of BAM neural networks with mixed delays and leakage time-varying delays in the weighted pseudo-almost periodic on time-space scales, Mathematical Methods in the Applied Sciences, 2018, 148(3): 1230–1255.
Author information
Authors and Affiliations
Corresponding authors
Additional information
This research was supported by the Natural Science Foundation of Shandong Province under Grant No. ZR2017MA045 and the National Natural Science Foundation of China under Grant No. 61873144.
This paper was recommended for publication by Editor WU Zhengguang.
Rights and permissions
About this article
Cite this article
Guo, Y., Ge, S.S. & Arbi, A. Stability of Traveling Waves Solutions for Nonlinear Cellular Neural Networks with Distributed Delays. J Syst Sci Complex 35, 18–31 (2022). https://doi.org/10.1007/s11424-021-0180-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-021-0180-7