Abstract
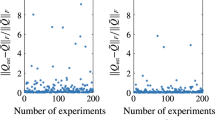
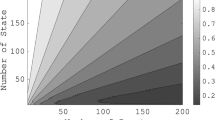
In this paper, the inverse linear quadratic (LQ) problem over finite time-horizon is studied. Given the output observations of a dynamic process, the goal is to recover the corresponding LQ cost function. Firstly, by considering the inverse problem as an identification problem, its model structure is shown to be strictly globally identifiable under the assumption of system invertibility. Next, in the noiseless case a necessary and sufficient condition is proposed for the solvability of a positive semidefinite weighting matrix and its unique solution is obtained with two proposed algorithms under the condition of persistent excitation. Furthermore, a residual optimization problem is also formulated to solve a best-fit approximate cost function from sub-optimal observations. Finally, numerical simulations are used to demonstrate the effectiveness of the proposed methods.
Similar content being viewed by others
References
Alexander R M, Optima for Animals, Princeton University Press, Princeton, New Jersey, 2021.
Heinrich B, Do bumblebees forage optimally, and does it matter?, American Zoologist, 1983, 23(2): 273–281.
Berret B and Jean F, Why don’t we move slower? the value of time in the neural control of action, Journal of Neuroscience, 2016, 36(4): 1056–1070.
Mombaur K, Truong A, and Laumond J P, From human to humanoid locomotionan inverse optimal control approach, Autonomous Robots, 2010, 28(3): 369–383.
Chittaro F C, Jean F, and Mason P, On inverse optimal control problems of human locomotion: Stability and robustness of the minimizers, Journal of Mathematical Sciences, 2013, 195(3): 269–287.
Priess M C, Conway R, Choi J, et al., Solutions to the inverse lqr problem with application to biological systems analysis, IEEE Transactions on Control Systems Technology, 2014, 23(2): 770–777.
Hadfield-Menell D, Russell S J, Abbeel P, et al., Cooperative inverse reinforcement learning, Advances in Neural Information Processing Systems, 2016, 29: 3909–3917.
Mainprice J, Hayne R, and Berenson D, Goal set inverse optimal control and iterative replanning for predicting human reaching motions in shared workspaces, IEEE Transactions on Robotics, 2016, 32(4): 897–908.
Berret B, Chiovetto E, Nori F, et al., Evidence for composite cost functions in arm movement planning: An inverse optimal control approach, PLoS Computational Biology, 2011, 7(10): e1002183.
Molloy T L, Ford J J, and Perez T, Finite-horizon inverse optimal control for discrete-time nonlinear systems, Automatica, 2018, 87: 442–446.
Panchea A M and Ramdani N, Towards solving inverse optimal control in a bounded-error framework, 2015 American Control Conference (ACC), IEEE, 2015, 4910–4915.
Pauwels E, Henrion D, and Lasserre J B, Linear conic optimization for inverse optimal control, SIAM Journal on Control and Optimization, 2016, 54(3): 1798–1825.
Mattila R, Rojas C R, Krishnamurthy V, et al., Inverse filtering for linear gaussian state-space models, 2018 IEEE Conference on Decision and Control (CDC), IEEE, 2018, 5556–5561.
Mattila R, Rojas C, Krishnamurthy V, et al., Inverse filtering for hidden markov models, Advances in Neural Information Processing Systems (NIPS) 2017, 2017, 30.
Mattila R, Rojas C R, Krishnamurthy V, et al., Inverse filtering for hidden markov models with applications to counter-adversarial autonomous systems, IEEE Transactions on Signal Processing, 2020, 68: 4987–5002.
Anderson B D O and Moore J B, Optimal Control: Linear Quadratic Methods, Prentice-Hall International Inc., Upper Saddle River, New Jersey, 1989.
Nori F and Frezza R, Linear optimal control problems and quadratic cost functions estimation, Proceedings of the 12th IEEE Mediterranean Conference on Control and Automation (MED’04), 2004, 6–9.
Jean F and Maslovskaya S, Inverse optimal control problem: The linear-quadratic case, 2018 IEEE Conference on Decision and Control (CDC), IEEE, 2018, 888–893.
Li Y B, Yao Y, and Hu X M, Continuous-time inverse quadratic optimal control problem, Automatica, 2020, 117: 108977.
Moylan P, Stable inversion of linear systems, IEEE Transactions on Automatic Control, 1977, 22(1): 74–78.
Morse A and Wonham W, Status of noninteracting control, IEEE Transactions on Automatic Control, 1971, 16(6): 568–581.
Biazar J, Babolian E, and Islam R, Solution of a system of volterra integral equations of the first kind by adomian method, Applied Mathematics and Computation, 2003, 139(2–3): 249–258.
Silverman L M J P, Inversion of multivariable linear systems, IEEE Transactions on Automatic Control, 1969, 14(3): 270–276.
Luenberger D G, Optimization by Vector Space Methods, John Wiley & Sons, New York, 1997.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Li, Y., Wahlberg, B. & Hu, X. Identifiability and Solvability in Inverse Linear Quadratic Optimal Control Problems. J Syst Sci Complex 34, 1840–1857 (2021). https://doi.org/10.1007/s11424-021-1245-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-021-1245-3