Abstract
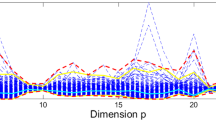
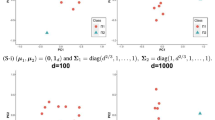
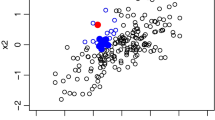
Outlier detection is a fundamental topic in robust statistics. Traditional outlier detection methods try to find a clean subset of given size, which is used to estimate the location vector and scatter matrix, and the outliers can be flagged by the Mahalanobis distance. However, methods such as the minimum covariance determinant approach cannot be applied directly to high-dimensional data, especially when the dimension of the sample is greater than the sample size. A novel fast detection procedure based on a block diagonal partition is proposed, and the asymptotic distribution of the modified Mahalanobis distance is obtained. The authors verify the specificity and sensitivity of this procedure by simulation and real data analysis in high-dimensional settings.
Similar content being viewed by others
References
Rousseeuw P J, Multivariate estimation with high breakdown point, Mathematical Statistics and Its Applications, Eds. by Grossmann W, Pflug G, Vincze I, et al., Reidel, 1985, B: 283–297.
Rousseeuw P J and Van Driessen K, A fast algorithm for the minimum covariance determinant estimator, Technometrics, 1999, 41: 212–223.
Cator E and Lopuhaä H, Central limit theorem and influence function for the MCD estimator at general multivariate distributions, Bernoulli, 2012, 18(2): 520–551.
Hardin J and Rocke D M, The distribution of robust distances, J. Comp. Graph. Statist, 2005, 14: 910–927.
Ro K, Zou C, Wang Z, et al., Outlier detection for high dimensional data, Biometrika, 2015, 102: 589–599.
Yang X, Wang Z, and Zi X, Thresholding-based outlier detection for high-dimensional data, Journal of Statistical Computation and Simulation, 2018, 88: 2170–2184.
Boudt K, Rousseeuw P J, Vanduffel S, et al., The minimum regularized covariance determinant estimator, Statistics and Computing, 2020, 30: 113–128.
Filzmoser P, Maronna R, and Werner M, Outlier identification in high dimensions, Comp. Statist. Data Anal, 2008, 52: 1694–1711.
Maronna R A, Martin R D, Yohai V J, et al., Robust Statistics Theory and Methods (with R), 2nd Edition, Wiley, Oxford, 2019.
Agulló J, Croux C, and Van Aelst S, The multivariate least-trimmed squares estimator, J. Mult. Anal, 2008, 99: 311–338.
Srivastava M S and Du M, A test for the mean vector with fewer observations than the dimension, J. Mult. Anal., 2008, 99: 386–402.
Lieb E H and Thirring W, Inequalities for the moments of the eigenvalues of the Schrödinger Hamiltonian and their relation to Sobolev inequalities, Studies in Mathematical Physics, Eds. by Lieb E, Simon B, and Wightman A, Princeton University Press, Princeton, 1976, 269–303.
Srivastava M S, Some tests concerning the covariance matrix in high-dimensional data, Journal of the Japan Statistical Society, 2005, 35: 251–272.
Pison G, Van Aelst S, and Willems G, Small sample corrections for LTS and MCD, Metrika, 2002, 55: 111–123.
Wu T, Liu S, and Zhou J, Statistical diagnosis for HIV dynamics based on mean shift outlier model, Journal of Systems Science & Complexity, 2015, 28(3): 592–605.
Xie L, Jia Y, Xiao J, et al., GMDH-based outlier detection model in classification problems, Journal of Systems Science & Complexity, 2020, 33(5): 1516–1532.
Esbensen K, Midtgaard T, and Schönkopf S, Multivariate Analysis in Practice: A Training Package, Camo As, Oslo, 1996.
Grübel R, A minimal characterization of the covariance matrix, Metrika, 1988, 35: 49–52.
Schott J R, Matrix Analysis for Statistics, Wiley, New York, 394.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the National Natural Science Foundation of China under Grant Nos. 71873128 and 72111530199.
This paper was recommended for publication by Editor LI Qizhai.
Rights and permissions
About this article
Cite this article
Li, C., Jin, B. Outlier Detection via a Block Diagonal Product Estimator. J Syst Sci Complex 35, 1929–1943 (2022). https://doi.org/10.1007/s11424-022-0298-2
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-022-0298-2