Abstract
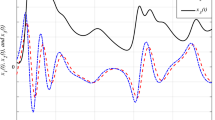
For a class of second-order sub-fully actuated systems (SOSFASs), this paper presents a preset-trajectory-based (PT-based) adaptive stabilising control method by integrating the function augmented sliding mode control (FASMC) technique and the flat-zone introduced Lyapunov function technique. The SOSFASs under study are subject to internal uncertainties and external disturbances. The proposed PT-based stabilising control method exhibits several attractive features: 1) The system states can converge to a predefined region close to zero in a preassigned time and can be confined in a preassigned ‘safe’ area, which can make the control coefficient matrix always full rank so as to preserve the realizability of the proposed controller; 2) the utilization of flat-zone introduced Lyapunov function technique not only eliminates the chatting phenomenon, but also avoids the potential persistent increase problem of the adaptive law; and 3) the control gain increases as the adaptive law increases only when necessary, that is, when the current control gain is not sufficient to suppress uncertainties or disturbances, therefore, the conservativeness of the control design due to unnecessarily high control gain can be effectively reduced. The effectiveness of the proposed control method is verified via a numerical example.
Similar content being viewed by others
References
Gholipour R and Fateh M M, Robust control of robotic manipulators in the task-space using an adaptive observer based on chebyshev polynomials, Journal of Systems Science & Complexity, 2020, 33(5): 1360–1382.
Duan G R, High-order system approaches: I. Fullactuation and parametric design, Acta Automatica Sinica, 2020, 46(7): 1333–1345 (in Chinese).
Duan G R, High-order fully actuated system approaches: Part I. Models and basic procedure, International Journal of System Sciences, 2021, 52(2): 422–435.
Duan G R, High-order system approaches: II. Controllability and fully-actuation, Acta Automatica Sinica, 2020, 46(8): 1571–1581 (in Chinese).
Duan G R, High-order system approaches: III. Observability and observer design, Acta Automatica Sinica, 2020, 46(9): 1885–1895 (in Chinese).
Duan G R, High-order fully actuated system approaches: Part VII. Controllability, stabilizability and parametric designs, International Journal of System Sciences, 2021, 52(14): 3091–3114.
Duan G R, High-order fully actuated system approaches: Part III. Robust control and high-order backstepping, International Journal of System Sciences, 2021, 52(5): 952–971.
Duan G R, High-order fully actuated system approaches: Part IV. Adaptive control and high-order backstepping, International Journal of System Sciences, 2021, 52(5): 972–989.
Duan G R, High-order fully actuated system approaches: Part V. Robust adaptive control, International Journal of System Sciences, 2021, 52(10): 2129–2143.
Duan G R, High-order fully actuated system approaches: Part VIII. Optimal control with application in spacecraft attitude stabilization, International Journal of System Sciences, 2022, 53(1): 54–73.
Duan G R, High-order fully-actuated system approaches: Part IX. Generalized PID control and model reference tracking, International Journal of System Sciences, https://doi.org/10.1080/00207721.2021.1970277.
Duan G R, Discrete-time delay systems: Part 2. Sub-fully actuated case, SCIENCE CHINA Information Sciences, 2021, DOI: https://doi.org/10.1007/s11432-021-3448-1.
Duan G R, High-order fully actuated system approaches: Part VI. Disturbance attenuation and decoupling, International Journal of System Sciences, 2021, 52(10): 2161–2181.
Park K B and Tsuji T, Terminal sliding mode control of second-order nonlinear uncertain systems, International Journal of Robust and Nonlinear Control, 1999, 9(11): 769–780.
Liu J K and Sun F C, A novel dynamic terminal sliding mode control of uncertain nonlinear systems, Journal of Control Theory and Applications, 2007, 5(2): 189–193.
Zhuang K Y, Su H Y, Zhang K Q, et al., Adaptive terminal sliding mode control for high-order nonlinear dynamic systems, Journal of Zhejiang University-SCIENCE A, 2003, 4(1): 58–63.
Hou M Z, Tan F, Han F, et al., Adaptive sliding mode control of uncertain nonlinear systems with preassigned settling time and its applications, International Journal of Robust and Nonlinear Control, 2019, 29(18): 6438–6462.
Cai G B, Li X Y, Hou M Z, et al., Improved function augmented sliding mode control of uncertain nonlinear systems with preassigned settling time, International Journal of Control, Automation and Systems, 2021, 19: 712–721.
Tran X T and Kang H J, Adaptive hybrid high-order terminal sliding mode control of MIMO uncertain nonlinear systems and its application to robot manipulators, International Journal of Precision Engineering and Manufacturing volume, 2015, 16(2): 255–266.
Author information
Authors and Affiliations
Corresponding author
Additional information
This research was supported by the National Natural Science Foundation of China under Grant No. 62073096, the Science Center Program of National Natural Science Foundation of China under Grant No. 62188101 and the Heilongjiang Touyan Team Program.
Rights and permissions
About this article
Cite this article
Shi, W., Hou, M. & Duan, GR. Adaptive Preassigned Time Stabilisation of Uncertain Second-Order Sub-Fully Actuated Systems. J Syst Sci Complex 35, 703–713 (2022). https://doi.org/10.1007/s11424-022-2042-3
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11424-022-2042-3