Skip to main content
Springer Nature Link
Log in

Discrete-time delayed standard neural network model and its application

  • Published:
Science in China Series F: Information Sciences Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

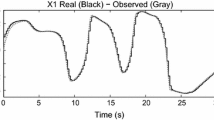
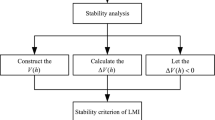
A novel neural network model, termed the discrete-time delayed standard neural network model (DDSNNM), and similar to the nominal model in linear robust control theory, is suggested to facilitate the stability analysis of discrete-time recurrent neural networks (RNNs) and to ease the synthesis of controllers for discrete-time nonlinear systems. The model is composed of a discrete-time linear dynamic system and a bounded static delayed (or non-delayed) nonlinear operator. By combining various Lyapunov functionals with the S-procedure, sufficient conditions for the global asymptotic stability and global exponential stability of the DDSNNM are derived, which are formulated as linear or nonlinear matrix inequalities. Most discrete-time delayed or non-delayed RNNs, or discrete-time neural-network-based nonlinear control systems can be transformed into the DDSNNMs for stability analysis and controller synthesis in a unified way. Two application examples are given where the DDSNNMs are employed to analyze the stability of the discrete-time cellular neural networks (CNNs) and to synthesize the neuro-controllers for the discrete-time nonlinear systems, respectively. Through these examples, it is demonstrated that the DDSNNM not only makes the stability analysis of the RNNs much easier, but also provides a new approach to the synthesis of the controllers for the nonlinear systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Suykens, J. A. K., Vandewall, J. P. L., De Moor, B. L. R., Artificial Neural Networks for Modeling and Control of Non-linear Systems, Norwell, MA: Kluwer Academic Publishers, 1996.

    Google Scholar 

  2. Juang, J. C., Stability analysis of Hopfield-type neural networks, IEEE Trans. on Neural Networks, 1999, 10(6): 1366–1374.

    Article  MathSciNet  Google Scholar 

  3. Li, X. M., Li, X. M., Exponential stability and global stability of cellular neural networks, Applied Mathematics and Computation, 2004, 147(3): 843–853.

    Article  MATH  MathSciNet  Google Scholar 

  4. Liao, X. X., Liao, Y., Liao, Y., Qualitative analysis of bidirectional associative memory neural networks, Journal of Electronics (in Chinese), 1998, 15(3): 208–214.

    Google Scholar 

  5. Liao, X. X., Liao, Y., Liao, Y., Stability of bidirectional associative memory neural networks with delays, Journal of Electronics (in Chinese), 1998, 15(4): 372–377.

    Google Scholar 

  6. Limanond, S., Si, J., Neural-network-based control design: An LMI approach, IEEE Transactions on Neural Networks, 1998, 9(6): 1422–1429.

    Article  Google Scholar 

  7. Miguel, A. B., Bart, W., Ton, V. D. B., Jose, S. D. C., Robust stability of feedback linearised systems modelled with neural networks: deal with uncertainty, Engineering Applications of Artificial Intelligence, 2000, 13(6): 659–670.

    Article  Google Scholar 

  8. Suykens, J. A. K., De Moor, B. L. R., Vandewalle, J. P. L., NLq theory: A neural control framework with global asymptotic stability criteria, Neural Networks, 1997, 10(4): 615–637.

    Article  Google Scholar 

  9. Boyd, S. P., Ghaoui, L. E., Feron, E., Balakrishnan, V., Linear Matrix Inequalities in System and Control Theory, Philadelphia, PA: SIAM, 1994.

    MATH  Google Scholar 

  10. Curran, P. F., Chua, L. O., Absolute stability theory and the synchronization problem, International Journal of Bifurcation and Chaos, 1997, 7(6): 1375–1382.

    Article  MATH  MathSciNet  Google Scholar 

  11. Barabanov, N. E., Prokhorov, D. V., Stability analysis of discrete-time recurrent neural networks, IEEE Trans. on Neural Networks, 2002, 13(2): 292–303.

    Article  Google Scholar 

  12. Liu, M. Q., Yan, G. F., Stability analysis of recurrent multiplayer perceptions: An LMI approach, Control Theory and Applications, 2003, 20(6): 897–902.

    MathSciNet  Google Scholar 

  13. Liu, M. Q., Zhang, S. L., Yan, G. F. et al., A new neural network model and its application, IEEE International Conference on Systems, Man and Cybernetics (SMC), October 10–13, 2004, The Hague, Netherlands, New York: IEEE Inc., 2004, 6: 5864–5869.

    Google Scholar 

  14. Liao, X. F., Chen, G. R., Sanchez, E. N., LMI-based approach for asymptotically stability analysis of delayed neural networks, IEEE Trans. on Circuits and Systems-I, 2002, 49(7): 1033–1039.

    Article  MathSciNet  Google Scholar 

  15. Liao, X. F., Chen, G. R., Sanchez, E. N., Delay-dependent exponential stability analysis of delayed neural networks: an LMI approach, Neural Networks, 2002, 15(7): 855–866.

    Article  MathSciNet  Google Scholar 

  16. Cao, J., Wang, J., Global asymptotic and robust stability of recurrent neural networks with time delays, IEEE Trans. on Circuits and Systems-I, 2005, 52(2): 417–426.

    Article  MathSciNet  Google Scholar 

  17. Liang, J., Cao, J., Daniel, W. C. H., Discrete-time bidirectional associative memory neural networks with variable delays, Physics Letters A, 2005, 335(2–3): 226–234.

    Article  MATH  Google Scholar 

  18. Cao, J., Liang, J., Lam, J., Exponential stability of high-order bidirectional associative memory neural networks with time delays, Physica D: Nonlinear Phenomena, 2004, 199(3–4): 425–436.

    Article  MATH  MathSciNet  Google Scholar 

  19. Cao, J., Wang, J., Absolute exponential stability of recurrent neural networks with time delays and Lipschitz-continuous activation functions, Neural Networks, 2004, 17(3): 379–390

    Article  MATH  Google Scholar 

  20. Cao J. Exponential stability and periodic solution of delayed cellular neural networks, Science in China, Series E, 2000, 43(3): 328–336.

    Article  MATH  MathSciNet  Google Scholar 

  21. Jin, C., Stability analysis of discrete-time Hopfield BAM neural networks, Acta Automatica Sinica, 1999, 25(5): 606–612.

    MathSciNet  Google Scholar 

  22. Wang, L., Zou, X. F., Capacity of stable periodic solutions in discrete-time bidirectional associative memory neural networks, IEEE Transactions on Circuits and System-II: Express Briefs, 2004, 51(6): 315–319.

    Article  Google Scholar 

  23. Qiu, S. S., Tsang, E. C. C. Yeung, D. S., Stability of discrete Hopfield neural networks with time-delay, 2002, IEEE International Conference on Systems, Man, and Cybernetics, 8–11 October 2002, 4: 2545–2550.

    Google Scholar 

  24. Gahinet, P., Nemirovski, A., Laub, A. J. et al., LMI Control Toolbox-for Use with Matlab, Natick, MA: The MATH Works, Inc., 1995.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Electrical Engineering, Zhejiang University, Hangzhou, 310027, China

    Liu Meiqin

Authors
  1. Liu Meiqin
    View author publications

    You can also search for this author inPubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, M. Discrete-time delayed standard neural network model and its application. SCI CHINA SER F 49, 137–154 (2006). https://doi.org/10.1007/s11432-006-0137-4

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11432-006-0137-4

Keywords