Abstract
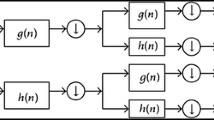
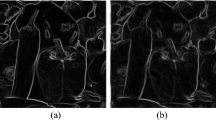
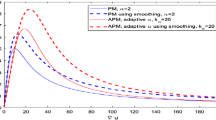
The nonlinear diffusion filtering in image processing bases on the heat diffusion equations. Its key is the control of diffusion amount. In the previous models, the diffusivity depends on the gradients of images. So it is easily affected by noises. This paper first gives a new multiscale computational technique for diffusivity. Then we proposed a class of nonlinear wavelet diffusion (NWD) models that are used to restore images. The NWD model has strong ability to resist noise. But it, like the previous models, requires higher computational effort. Thus, by simplifying the NWD, we establish linear wavelet diffusion (LWD) models that consist of advection and diffusion. Since there exists the advection, the LWD filter is anisotropic, and hence can well preserve edges although the diffusion at edges is isotropic. The advantage is that the LWD model is easy to be analyzed and has lesser computational load. Finally, a variety of numerical experiments compared with the previous model are shown.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE TPAMI, 1990, 12(7): 629–639
Catté F, Lions P L, Morel J M, et al. Image selective smoothing and edge detection by nonlinear diffusion. SIAM J Numerical Anallysis, 1992, 29: 182–193
Weickert J. Nonlinear diffusion scale-spaces: From the continuous to discrete setting. In: Berger M O, ed. Proc ICAOS’96: Images, Wavelets and PDE’s 219. New York: Springer, 1996. 111–118
Weickert J. Efficient and reliable schemes for nonlinear diffusion filtering. IEEE Trans On Image Processing, 1998, 7(3): 398–410
Weickert J. Theoretical foundations of anisotropic diffusion in image processing. Computing, 1996, 11(Suppl.): 221–236
Clarenz U, Diewald U, Rumpf M. Processing textured surfaces via anisotropic geometric diffusion. IEEE Trans On Image Processing, 2004, 13(2): 248–261
Alvarez L, Lions P L, Morel J M. Image selective smoothing and edge detection by nonlinear diffusion II. SIAM J Numer Anal, 1992, 29(3): 845–866
Alvarez L, Guichard F, Lions P L, et al. Axioms and fundamental equations of image processing. Arch Ration Mech Anal, 1993, 123: 199–257
Mrazek P, Weickert J, Steidl G. Correspondences between wavelet shrinkage and nonlinear diffusion. In: Griffin L D, Lillholm M, eds. Scale-Space 2003, LNCS 2695. Berlin: Springer-Verlag, 2003. 101–116
Chan T F, Zhou H M. Total variation improved wavelet thresholding in image compression. Proceeding Seventh International Conf on Image Processing, 2000, 2: 391–394
Malgouyres F. Combining total variation and wavelet packet approaches for image deblurring. Proc IEEE Workshop, 2001, 57–64
Iijima T. Basic theory of pattern normalization (for the case of a typical one-dimensional pattern). Bull Electrotech Lab (in Japanese), 1962, 26: 368–388
Peng L Z, Wang Y G. Construction of compactly supported orthonormal wavelets with beautiful structure. Sci China Ser F-Inf Sci, 2004, 47(3): 372–383
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Liu, F. Diffusion filtering in image processing based on wavelet transform. SCI CHINA SER F 49, 494–503 (2006). https://doi.org/10.1007/s11432-006-0494-z
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11432-006-0494-z