Skip to main content
Springer Nature Link
Log in

The essential order of approximation for nearly exponential type neural networks

  • Published:
Science in China Series F: Information Sciences Aims and scope Submit manuscript

Abstract

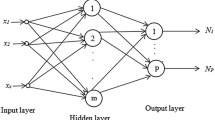
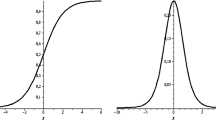
For the nearly exponential type of feedforward neural networks (neFNNs), it is revealed the essential order of their approximation. It is proven that for any continuous function defined on a compact set of R d, there exists a three-layer neFNNs with fixed number of hidden neurons that attain the essential order. When the function to be approximated belongs to the α-Lipschitz family (0 < α ⩽ 2), the essential order of approximation is shown to be O(n −α) where n is any integer not less than the reciprocal of the predetermined approximation error. The upper bound and lower bound estimations on approximation precision of the neFNNs are provided. The obtained results not only characterize the intrinsic property of approximation of the neFNNs, but also uncover the implicit relationship between the precision (speed) and the number of hidden neurons of the neFNNs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Attali J G, Pages G. Approximation of functions by a multilayer perception: A new approach. Neural Networks, 1997, 10: 1069–1081

    Article  Google Scholar 

  2. Cardaliaguet P, Euvrard G. Approximation of a function and its derivatives with a neural networks. Neural Networks, 1992, 5: 207–220

    Article  Google Scholar 

  3. Cao F L, Xu Z B. Neural network approximation for multivariate periodic functions: estimates on approximation order. Chinese Journal of Computers, 2001, 24(9): 903–908

    MathSciNet  Google Scholar 

  4. Chui C K, Li X. Approximation by ridge functions and neural networks with one hidden layer. J Approx Theory, 1992, 70: 131–141

    Article  MATH  MathSciNet  Google Scholar 

  5. Chui C K, Li X. Neural networks with one hidden layer. In: Multivariate Approximation. Jetter K, Utreras F I, eds. From CAGD to Wavelets. Singapore: World Scientific Press, 1993. 77–89

    Google Scholar 

  6. Chen T P, Chen H. Universal approximation to nonlinear operators by neural networks with arbitrary activation functions and its application to a dynamic system. IEEE Transaction on Neural Networks, 1995, 6: 911–917

    Article  Google Scholar 

  7. Chen T P. Approximation problems in system identification with neural networks, Sci China Ser A-Math, 1994, 24(1): 1–7

    Google Scholar 

  8. Hornik K, Stinchombe M, White H. Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Networks, 1990, 3: 551–560

    Article  Google Scholar 

  9. Jackson D. On the approximation by trigonometric sums and polynomials. Trans Amer Math Soc, 1912, 13: 491–515

    Article  MATH  MathSciNet  Google Scholar 

  10. Cybenko G. Approximation by superpositions of sigmoidal function. Math of Control Signals and System, 1989, 2: 303–314

    MATH  MathSciNet  Google Scholar 

  11. Funahashi K I. On the approximate realization of continuous mappings by neural networks. Neural Networks, 1989, 2: 183–192

    Article  Google Scholar 

  12. Yoshifusa I, Approximation of functions on a compact set by finite sums of sigmoid function without scaling. Neural Networks, 1991, 4: 817–826

    Article  Google Scholar 

  13. Kurkova V, Kainen P C, Kreinovich V. Estimates for the number of hidden units and variation with respect to half-space. Neural Networks, 1997, 10: 1068–1078

    Article  Google Scholar 

  14. Mhaskar H N, Micchelli C A. Approximation by superposition of a sigmoidal function. Advances in Applied Mathematics, 1992, 13: 350–373

    Article  MATH  MathSciNet  Google Scholar 

  15. Mhaskar H N. Neural networks for optimal approximation for smooth and analytic functions. Neural Comput, 1996, 8: 164–177

    Google Scholar 

  16. Mhaskar H N, Micchelli C A. Degree of approximation by neural networks with a single hidden layer. Advances in Applied Mathematics, 1995, 16: 151–183

    Article  MATH  MathSciNet  Google Scholar 

  17. Mhaskar H N, Khachikyan L. Neural networks for functions approximation. In: Makhoul J, Manolakos E, Wilson E, eds. Neural Networks for Signal Processing, Proc. 1995 IEEE Workshop, Vol. V, F. Girosi (Cambridge, MA). New York: IEEE Press, 1995. 21–29

    Google Scholar 

  18. Mhaskar H N, Micchelli C A. Dimension-independent bounds on the degree of approximation by neural networks. IBM J Res Develop, 1994, 38: 277–284

    Article  MATH  Google Scholar 

  19. Maiorov V, Meir R S. Approximation bounds for smooth functions in C(R d) by neural and mixture networks. IEEE Trans on Neural Networks, 1998, 9: 969–978

    Article  Google Scholar 

  20. Suzuki S. Constructive function approximation by three-layer artificial neural networks. Neural Networks, 1998, 11: 1049–1058

    Article  Google Scholar 

  21. Ritter G. Jackson’s theorems and the number of hidden units in Neural networks for uniform approximation. Univ Passau, Fak Math Inform, Technical Report, MIP9415, 1994

  22. Xu Z B, Cao F L. The essential order of approximation for neural networks. Sci China Ser F-Inf Sci, 2004, 47: 97–112

    Article  MathSciNet  MATH  Google Scholar 

  23. Ritter G. Efficient estimation of neural weights by polynomial approximation. IEEE Trans on Information Theory, 1999, 45: 1541–1550

    Article  MATH  MathSciNet  Google Scholar 

  24. Feinerman R P, Newman D J. Polynomial Approximation. Baltimore, MD: Williams & Wilkins, 1974

    MATH  Google Scholar 

  25. Nikol’skii S M. Approximation of functions of several variables and imbedding theorems. Berlin, Heidelberg, New York: Springer, 1975

    Google Scholar 

  26. Soardi P M. Serie di fouroer in piú variabili. Quad dell’Unione Mat Italiana, Vol. 26. Bologna: Pitagora Editrice, 1984

    Google Scholar 

  27. Ditzian Z, Totik V. Moduli of Smoothness, New York: Springer-Verlag, 1987

    MATH  Google Scholar 

  28. Johnen H, Scherer K. On the equivalence of the K-functional and modulus of continuity and some applications. In: Schempp W, Zeller K eds. Constructive Theory of Functions of Several Variable. Berlin: Springer-Verlag, 1977. 119–140

    Google Scholar 

  29. Hornik K, Stinchombe M, White H. Multilayer feedforward networks are universal approximation. Neural Networks, 1989, 2: 359–366

    Article  Google Scholar 

  30. Leshno M, Lin V Y, Pinks A, Schocken S. Multilayer feedforward networks with a nonpolynomial activation function can approximate any function. Neural Networks, 1993, 6: 861–867

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute for Information and System Science, Xi’an Jiaotong University, Xi’an, 710049, China

    Xu Zongben & Wang Jianjun

Authors
  1. Xu Zongben
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wang Jianjun
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xu Zongben.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Xu, Z., Wang, J. The essential order of approximation for nearly exponential type neural networks. SCI CHINA SER F 49, 446–460 (2006). https://doi.org/10.1007/s11432-006-2011-9

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11432-006-2011-9

Keywords