Skip to main content

Advertisement

Springer Nature Link
Log in

MIMO-OFDM system based on fractional Fourier transform and selecting algorithm for optimal order

  • Published:
Science in China Series F: Information Sciences Aims and scope Submit manuscript

Abstract

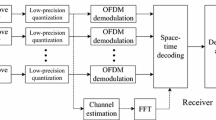
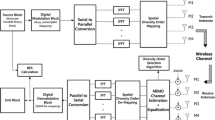
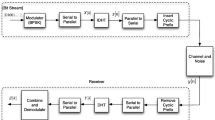
In the rapidly time-varying channel environment, the performance of traditional MIMO-OFDM system is deteriorated due to the intercarrier interference. In this paper, a novel MIMO-OFDM system is proposed, in which the modulation and demodulation of the symbols are implemented by the fractional Fourier transform instead of traditional Fourier transform. Through selecting the optimal order of the fractional Fourier transform, the modulated signals can match the time-varying channel characteristics, which results in a mitigation of the intercarrier interference. Furthermore, an algorithm is presented for selecting the optimal order of fractional Fourier transform, and the impact of system parameters on the optimal order is analyzed. Simulation results show that the proposed system can concentrate the power of desired signal effectively and improve the performance over rapidly time-varying channels with respect to the traditional MIMO-OFDM system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Foschini G J, Gans M J. On limits of wireless communication in a fading environment when using multiple antennas. Wirel Pers Commun, 1998, 6(3): 311–335

    Article  Google Scholar 

  2. Jankiraman M. Space-Time Codes and MIMO Systems. Boston-London: Artech House Publishers, 2004. 1–12

    Google Scholar 

  3. Wang Z, Giannakis G B. Wireless multicarrier communications: where Fourier meets Shannon. IEEE Signal Process Mag, 2000, 17(3): 29–48

    Article  Google Scholar 

  4. Stuber G L, Barry J R, McLaughlin S W, et al. Broadband MIMO-OFDM Wireless Communications. Proc IEEE, 2004, 92(2): 271–294

    Article  Google Scholar 

  5. Stamoulis A, Diggavi S N Al-Dhahir N. Intercarrier Interference in MIMO OFDM. IEEE Trans Signal Process, 2002, 50(10): 2451–2464

    Article  Google Scholar 

  6. Song L J, Mohsen K. Effects of time selective multipath fading on OFDM systems for broadband mobile application. IEEE Commun Lett, 1999, 3(12): 332–334

    Article  Google Scholar 

  7. Vahlin A, Holte N. Optimal finite duration pulses for OFDM. IEEE Trans Commun, 1996, 44(1): 10–14

    Article  MATH  Google Scholar 

  8. Kozek W, Molisch A. Nonorthogonal pulseshapes for multicarrier communications in doubly dispersive channels. IEEE J Sel Area Commun, 1998, 16(8): 1579–1589

    Article  Google Scholar 

  9. Strohmer T, Beaver S. Optimal OFDM design for time-frequency dispersive channels. IEEE Trans Commun, 2003, 51(7): 1111–1122

    Article  Google Scholar 

  10. Martone M. A multicarrier system based on the fractional Fourier transform for time-frequency selective channels. IEEE Trans Commun, 2001, 49(6): 1011–1020

    Article  MATH  Google Scholar 

  11. Almeida L B. The fractional Fourier transform and time-frequency representations. IEEE Trans Signal Process, 1994, 42(11): 3084–3091

    Article  Google Scholar 

  12. Ozaktas H M, Zalevsky Z, Kutay M A. The Fractional Fourier Transform with Applications in Optics and Signal Processing. New York: Wiley, 2000. 319–464

    Google Scholar 

  13. Lohmann A W. Image rotation, Wigner rotation, and the fractional Fourier transform. J Opt Soc Amer A, 1993, 10: 2181–2186

    Article  Google Scholar 

  14. Ozaktas H M, Barshan B, Mendlovic D, et al. Convolution, filtering, and multiplexing in fractional Fourier domains and their relationship to chirp and wavelet transform. J Opt Soc Amer A, 1994, 11: 547–559

    MathSciNet  Google Scholar 

  15. Tao R, Deng B, Wang Y. Research progress of the fractional Fourier in signal processing. Sci China Ser F-Inf Sci, 2006, 49(1): 1–25

    Article  MATH  MathSciNet  Google Scholar 

  16. Tao R, Qi L, Wang Y. Theory and Application of the Fractional Fourier Transform (in Chinese). Beijing: Tsinghua University Press, 2004. 111–175

    Google Scholar 

  17. Ozaktas H M, Arikan O, Kutay M A, et al. Digital computation of the fractional Fourier transform. IEEE Trans on Signal Process, 1996, 44(9): 2141–2150

    Article  Google Scholar 

  18. Pei S C, Ding J J. Closed-form discrete fractional and affine Fourier transforms. IEEE Trans Signal Process, 2000, 48(5): 1338–1353

    Article  MATH  MathSciNet  Google Scholar 

  19. Santhanam B, McClellan J H. The discrete rotational Fourier transform. IEEE Trans Signal Process, 1996, 42: 994–998

    Article  Google Scholar 

  20. Kraniauskas P, Cariolaro G, Erseghe T. Method for defining a class of fractional operations. IEEE Trans Signal Process, 1998, 46: 2804–2807

    Article  MATH  MathSciNet  Google Scholar 

  21. Deng X G, Li Y P, Fan D Y, et al. A fast algorithm for fractional Fourier transforms. Opt Commun, 1997, 138: 270–274

    Article  Google Scholar 

  22. Pei S C, Yeh M H. Discrete fractional Fourier transform. In: Proc IEEE Int Symp Circ Syst. Washington: IEEE, 1996. 536–539

    Google Scholar 

  23. Pei S C, Yeh M H. Improved discrete fractional Fourier transform. Opt Lett, 1997, 22: 1047–1049

    Article  Google Scholar 

  24. Chen E Q. Research on the key techniques for the OFDM system based on the fractional Fourier transform. Doctoral Dissertation. Beijing: Beijing Institute of Technology, 2006. 39–40

    Google Scholar 

  25. Moose H. A technique for orthogonal frequency-division multiplexing frequency offset correction. IEEE Trans Commun, 1994, 42(10): 2908–2914

    Article  Google Scholar 

  26. Zhang Y, Liu H P. Impact of time-selective fading on the performance of quasi-orthogonal space-time-coded OFDM systems. IEEE Trans Commun, 2006, 54(2): 251–260

    Article  Google Scholar 

  27. Pop M F, Norman C. Beaulieu. limitations of sum-of-sinusoids fading channel simulators. IEEE Trans Commun, 2001, 49(4): 699–708

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Electronic Engineering, Beijing Institute of Technology, Beijing, 100081, China

    Qian Yang, Ran Tao & Yue Wang

  2. The College of Information Engineering, Zhengzhou University, Zhengzhou, 450052, China

    EnQing Chen

Authors
  1. Qian Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Ran Tao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yue Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. EnQing Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ran Tao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, Q., Tao, R., Wang, Y. et al. MIMO-OFDM system based on fractional Fourier transform and selecting algorithm for optimal order. Sci. China Ser. F-Inf. Sci. 51, 1360–1371 (2008). https://doi.org/10.1007/s11432-008-0123-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11432-008-0123-0

Keywords