Skip to main content
SpringerLink
Log in

Gaussian-curvature-derived invariants for isometry

  • Research Paper
  • Published:
Science China Information Sciences Aims and scope Submit manuscript

Abstract

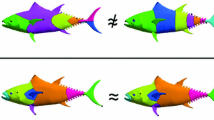
Surface deformations without tearing or stretching, preserving the intrinsic properties, are called isometries. This paper presents a new definition of Gaussian curvature moments (GCMs) by the integral of n power of Gaussian curvature. Then a series of moment invariants, called Gaussian curvature moment invariants (GCMIs), are derived via GCMs. These moment invariants share many good properties under rigid transformations and isometric non-rigid transformations, and Gaussian-Bonnet theorem is a special case of GCMI. GCMIs are invariant under isometry and scaling transformations. We construct an invariant vector as a descriptor for a surface via GCMIs, and a modified χ 2 distance is defined as a measure of similarity. Finally, experiments show that it is a reliable descriptor for isometric non-rigid shape.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. O’Neill B. Elementary Differential Geometry. Revised Second Edition. Waltham, Massachusetts: Academic Press (Elsevier), 2006

    MATH  Google Scholar 

  2. Sadjadi F, Hall E. Three-dimensional moment invariants. IEEE Trans Patt Anal Mach Intell, 1980, 2: 127–136

    Article  MATH  Google Scholar 

  3. Xu D, Li H. Geometric moment invariant. Patt Recog, 2008, 41: 240–249

    Article  MATH  Google Scholar 

  4. Canterakis N. 3D zernike moments and zernike affine invariants for 3D image analysis and recognition. In: 11th Scandinavian Conference on Image Analysis, Kangerlussuaq, Greenland, 1999. 85–93

  5. Osada R, Funkhouser T, Chazelle B, et al. Shape distributions. ACM Trans Graph, 2002, 21: 807–832

    Article  Google Scholar 

  6. Funkhouser T, Min P, Kazhdan M, et al. A search engine for 3D models. ACM Trans Graph, 2003, 22: 83–105

    Article  Google Scholar 

  7. Horn B. Extended Gaussian image. Proc IEEE, 1984, 12: 1671–1686

    Article  Google Scholar 

  8. Johnson A, Hebert M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans Patt Anal Mach Intell, 1999, 21: 433–449

    Article  Google Scholar 

  9. Vránic D, Saupe D D. 3D shape descriptor based on 3D Fourier transform. In: Proceedings of the EURASIP Conference on Digital Signal Processing for Multimedia Communications and Services (ECMCS 2001), Budapest, Hungary, 2001. 271–274

  10. Paquet E, Murching A, Naveen T, et al. Description of shape information for 2-D 3-D objects. Signal Process Image Commun J, 2000, 16: 103–122

    Article  Google Scholar 

  11. Sundar H, Silver D, Gagvani N, et al. Skeleton based shape matching and retrieval. In: Shape Modeling and Applications Conference, Seoul, Korea. IEEE Computer Society, 2003. 130–142

    Google Scholar 

  12. Ip H, Wong W. 3D head models retrieval based on hierarchical facial region similarity. In: Proceedings of the 15th International Conference on Vision Interface, Calgary, Canada, 2002. 314–319

  13. Adan A, Adan M. A flexible similarity measure for 3D shapes recognition. IEEE Trans Patt Anal Mach Intell, 2004, 26: 1507–1520

    Article  Google Scholar 

  14. Hilaga M, Shinagawa Y, Komura T, et al. Topology matching for fully automatic similarity estimation of 3D shapes. In: Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 2001. 203–212

  15. Hamza A, Krim H. Geodesic object representation and recognition. In: International Conference on Discrete Geometry for Computer Imagery, Naples, 2003. 2886: 378–387

  16. Elad A, Kimmel R. On bending invariant signatures for surfaces. IEEE Trans Patt Anal Mach Intell, 2003, 26: 1285–1295

    Article  Google Scholar 

  17. Bronstein A, Bronstein M, Kimmel R. Generalized multidimensional scaling: a framework for isometry-invariant partial surface matching. Proc Nat Acad Sci (PNAS), 2006, 103: 1168–1172

    Article  MathSciNet  MATH  Google Scholar 

  18. Bronstein A, Bronstein M, Kimmel R. Numerical Geometry of Non-Rigid Shapes. Berlin: Springer, 2008

    MATH  Google Scholar 

  19. Mémolif F, Sapiro G. A theoretical and computational framework for isometry invariant recognition of point cloud data. Found Comput Math, 2005, 5: 313–347

    Article  MathSciNet  Google Scholar 

  20. Memoli F. On the use of Gromov-Hausdorff distances for shape comparison. In: Proceedings of EG/IEEE Symposium on Point-Based Graphics, Prague, Czech, 2007. 81–90

  21. Bronstein A, Bronstein M, Kimmel R. Efficient computation of isometry-invariant distances between surfaces. SIAM J Sci Comput, 2006, 28: 1812–1836

    Article  MathSciNet  MATH  Google Scholar 

  22. Bronstein A, Bronstein M, Kimmel R, et al. A Gromov-Hausdorff framework with diffusion geometry for topologicallyrobust non-rigid shape matching. Int J Comput Vision, 2010, 89: 266–286

    Article  Google Scholar 

  23. Bronstein M, Bronstein A. Shape recognition with spectral distances. IEEE Trans Patt Anal Mach Intell, 2011, 33: 1065–1071

    Article  Google Scholar 

  24. Reuter M, Wolter F, Peinecke N. Laplace-Beltrami spectra as ‘Shape-DNA’ of surfaces and solids. Comput-Aid Design, 2006, 38: 342–366

    Article  Google Scholar 

  25. Reuter M, Biasotti S, Giorgi D, et al. Discrete Lapalece-Beltrami operators for shape analysis and segmentation. Comput Graph, 2009, 33: 381–390

    Article  Google Scholar 

  26. Rustamov R. Laplace-Beltrami eigenfunctions for deformation invariant shape representation. In: Proceedings Symposium on Geometry Processing (SGP), Barcelona, Spain, 2007. 225–233

  27. Ruggeri M, Saupe D. Isometry-invariant matching of point set surfaces. In: Proceedings Eurographics Workshop on 3D Object Retrieval, Crete, Greece, 2008

  28. Polonsky O, Patane G, Biasotti S, et al. What’s in an image: towards the computation of the “best” view of an object. Visual Comput, 2005, 21: 840–847

    Article  Google Scholar 

  29. Yamauchi H, Gumhold S, Zayer R, et al. Mesh segmentation driven by Gaussian curvature. Visual Comput, 2005, 21: 659–668

    Article  Google Scholar 

  30. Ip C, Regli W. A 3D object classifier for discriminating manufacturing processes. Comput Graph, 2006, 30: 903–916

    Article  Google Scholar 

  31. Sukumar S, Page D, Koschan A, et al. Shape measure for identifying perceptually informative parts of 3D objects. In: Proc. IEEE 3rd International Symposium on 3D Data Processing, Visualization and Transmission 3DPVT, Chapel Hill, NC, 2006. 679–686

  32. Tosranon P, Sanpanich A, Bunluechokchai C, et al. Gaussian curvature-based geometric invariance. In: The 6th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information technology, Chonburi Thailand, 2009. 1124–1127

  33. Guo K, Li M. A novel shape descriptor: Gaussian curvature moment invariants. In: The 1st International Conference on Information Science and Engineering (ICISE2009), Nanjing, China, 2009. 1087–1090

  34. Pottmann H, Wallner J, Huang Q, et al. Integral invariants for robust geometry processing. Comput Aided Geom D, 2009, 26: 37–60

    Article  MathSciNet  MATH  Google Scholar 

  35. Xu G. Convergence analysis of a discretization scheme for Gaussian curvature over triangular surfaces. Comput Aid Geometric Design, 2006, 23: 193–207

    Article  MATH  Google Scholar 

  36. Surazhsky T, Magid E, Soldea O, et al. A comparison of Gaussian and mean curvatures estimation methods on triangular meshes. In: 2003 IEEE International Conference on Robotics & Automation (ICRA2003), Taipei, Taiwan, China, 2003. 1021–1026

  37. Sumner R W, Popovic J. Deformation transfer for triangle meshes. ACM Trans Graph, 2004, 23: 399–405

    Article  Google Scholar 

  38. Mahmoudi M, Sapiro G. Three-dimensional point cloud recognition via distributions of geometric distances. Graph Models, 2009, 71: 22–31

    Article  Google Scholar 

  39. Surazhsky V, Surazhsky T, Kirsanov D, et al. Fast exact and approximate geodesics on meshes. ACM Trans Graph, 2005, 24: 553–560

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computing Technology, Chinese Academy of Sciences, Beijing, 100190, China

    WeiGuo Cao, Ping Hu, Ming Gong & Hua Li

  2. Graduate University of Chinese Academy of Sciences, Beijing, 100190, China

    WeiGuo Cao, Ping Hu, Ming Gong & Hua Li

  3. School of Computer Science and Communication Engineering, China University of Petroleum, Dongying, 257061, China

    YuJie Liu

Authors
  1. WeiGuo Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ping Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. YuJie Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ming Gong
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Hua Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to WeiGuo Cao or Ping Hu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Cao, W., Hu, P., Liu, Y. et al. Gaussian-curvature-derived invariants for isometry. Sci. China Inf. Sci. 56, 1–12 (2013). https://doi.org/10.1007/s11432-011-4453-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11432-011-4453-y

Keywords

Search

Navigation