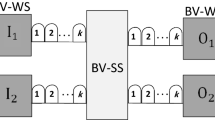
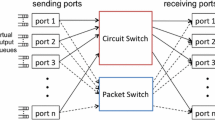
Abstract
Switching units and networks have been analyzed as extensible fabrics, mostly in terms of their scheduling algorithms. The traditional literature on switching extensibility has provided complexity theory only relating to the total numbers of inputs (or outputs) and exchange lines. This paper analyzes switching extensibility in terms of not only the scheduling algorithm and also the fabric itself. It is found that determining extensibility from soft complexity related to the number of inputs (or outputs) of the scheduling algorithm and the fabric extensibility in previous studies without quantization is a flawed conception. A method is thus proposed to express the spatial extensibility of a switching unit or network in terms of the connections of a switching resource and capacity. The method calculates parameter ES (the efficiency of switching) of an m× n switching unit and obtains two functions of the switching unit to describe spatial extensibility along with the number of unilateral inputs or outputs. It is found that the range of ES is (0, 1] and three types of switching unit and two types of crosspoint networks have ES = 1. ES is calculated for banyan, Clos, parallel packet, fully interconnected and recirculation switching networks. The ES value for the banyan switching network is larger than that for other networks, and switching networks are classified into three types that have absolute/linear/denied spatial extensibility according to the limES value. It is demonstrated that a switching network has the largest ES value when it contains only the five types of switching unit for which ES = 1. Finally, a group-switching-first self-routing banyan switching network with lower blocking probability and time delay is deduced, and the ES method is contrasted with two other methods of evaluating spatial extensibility in terms of their mathematical expressions and intuitive graphics, for the five types of switching network listed above.
Similar content being viewed by others
References
Chang C S, Cheng J, Lee D S, et al. Quasi-output-buffered switches. IEEE Trans Parall Distr, 2011, 22: 833–846
Lee Y, Lou J Y, Luo J Z, et al. An efficient packet scheduling algorithm with deadline guarantees for input-queued switches. IEEE/ACM Trans Network, 2007, 15: 212–225
Giaccone P, Prabhakar B, Shah D. Towards simple, high-performance schedulers for high-aggregate bandwidth switches. In: Proceedings of IEEE INFOCOM 2002. New York: IEEE Press, 2002. 1160–1169
Wang X L, Cai Y, Xiao S, et al. A three-stage load-balancing switch. In: Proceedings of IEEE INFOCOM. Phoenix: IEEE Press, 2008. 1993–2001
Firoozshahian A, Manshadi V, Goel A, et al. Efficient, fully local algorithms for CIOQ switches. In: Proceedings of IEEE INFOCOM. Anchorage: IEEE Press, 2007. 2491–2495
Neely M J, Modiano E, Cheng Y S. Logarithmic delay for N × N packet switches under the crossbar constraint. IEEE/ACM Trans Network, 2007, 15: 657–668
He S M, Sun S T, Guan H T, et al. On guaranteed smooth switching for buffered crossbar switches. IEEE/ACM Trans Network, 2008, 16: 718–731
Lee T H. Design and analysis of a new self-routing network. IEEE/ACM Trans Comm, 1992, 40: 171–177
Coppo P, D’Ambrosio M, Melen R. Optimal cost/performance design of ATM switches. IEEE/ACM Trans Network, 1993, 1: 566–575
He F Y, Wen M S. Analyzing hardware complexity of rapid package switching based on banyan network. Commun J, 1996, 17: 27–33
Roberto R C, Lin C B. Scalable two-stage clos-network switch and module-first matching. In: Proceedings of IEEE Workshop on High Performance Switching and Routing. Poznan: IEEE Press, 2006. 6–11
Meloni P, Murali S, Carta S, et al. Routing aware switch hardware customization for networks on chips. In: Proceedings of IEEE 1st International Conference on Nano-Networks. Lausanne: IEEE Press, 2006. 1–5
Xu Z G, Ren K X, Yu F. Design and analysis of 2-Omega novel conference component network. Comput Eng, 2010, 36: 96–100
Li S Y R. Algebraic Switching Theory and Broadband Applications. Salt Lake City: Academic Press, 2001. 10–21
Actel Corporation. Designing high-speed ATM switching fabrics by using actel FPGAs. Application Note AC105, 1996. 19–26
VSC880 datasheet rev 4.0: high performance 16×16 serial crosspoint switch. Online available at: http://www.vitesse.com
BNT virtual fabric 10Gb switch module for IBM blade center powerPRS. IBM Blade Center, 2011. http://www.ibm.com/redbooks/abstracts/tips0708.html
Li X Z, Yang H G. Design of intercross switch in FPGA chip. Microelectron J, 2007, 37: 606–609
Turner J S, Wyatt L F. A packet network architecture for integrated services. In: Proceedings of IEEE GLOBECOM. California: IEEE Press, 1983. 2.1.1–2.1.6
Kulzer J J, Montgomery W A. Statistical switching architecture for future services. In: Proceedings of AFIPS-National Computer. Chicago: AFIPS Press, 1985. 175–181
Iyer S, McKeown N. Analysis of a packet switch with the memories running slower than the line rate. In: Proceedings of IEEE INFOCOM’2000. Israel: IEEE Press, 2000. 529–537
Li H, He W, Yi P, et al. Modeling multi-path self-routing switching structure from multistage interconnection of sorting concentrators. ACTA Electron Sin, 2008, 36: 1–8
Li S Y R. Unified algebraic theory of sorting, routing, multicasting, and concentration networks. IEEE Trans Commun, 2010, 58: 247–256
Li S Y R, Tan X S. On rearrangeability of tandem connection of Banyan-type networks. IEEE Trans Commun, 2009, 57: 164–170
Hu H C, Yi P, Guo Y F. Design and implementation of high performance simulation platform for switching and scheduling. J Softw, 2008, 19: 1036–1050
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Zhang, B., Wu, J., Wang, B. et al. A method to evaluate the spatial extensibility of a switching unit and network. Sci. China Inf. Sci. 57, 1–17 (2014). https://doi.org/10.1007/s11432-012-4734-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11432-012-4734-0