Abstract
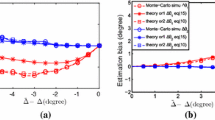
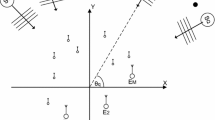
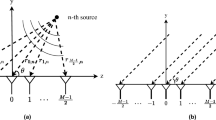
In this paper, a new method for fast direction-of-arrival (DOA) estimation with no dependance on array configurations is proposed, which is referred to as the symmetrical multiple signal classification (SMUSIC). Unlike the standard MUSIC, the S-MUSIC spatial spectrum is constructed by the intersection of the noise subspace and the conjugate noise subspace, and it hence generates spectral peaks at the true DOAs and the symmetrical virtual DOAs simultaneously. Such a characteristic allows fast DOA estimation by spectral search over only half of the total angular filed-of-view. Therefore, the new approach has a much lower computational complexity than the standard MUSIC. The statistical performance of S-MUSIC is studied and a close-form expression for the MSEs (mean square errors) of DOA estimation by the proposed estimator is derived. Numerical simulations are conducted to demonstrate the effectiveness of the new algorithm and to verify the theoretical analysis, and it is indicated that S-MUSIC makes a trade-off between MSEs and lower computational complexity as well as an improved resolution for closely-spaced sources as compared to the standard MUSIC.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Schmidt R O. Multiple emitter location and signal parameter estimation. IEEE Trans Antennas Propag, 1986, 34: 276–280
Jaffer A G. Maximum likelihood direction finding of stochastic sources: a separable solution. In: Proceedings of International Conference on Acoustics, Speech, and Signal Processing, New York, 1988. 2893–2896
Viberg M, Ottersten B. Sensor array processing based on subspace fitting. IEEE Trans Signal Process, 1991, 39: 1101–1121
Kumaresan R, Tufts D W. Estimating the angles of arrival of multiple plane waves. IEEE Trans Aerosp Electron Syst, 1983, AES-19: 134–139
Zhang Y, Ng B P. MUSIC-Like DOA Estimation without Estimating the Number of Sources. IEEE Trans Signal Process, 58: 1668–1676
Wong K T, Zoltowski M D. Self-initiating MUSIC-based direction finding and polarization estimation in spatiopolarizational beamspace. IEEE Trans Antennas Propag, 2000, 48: 1235–1245
Stoica P, Nehorai A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans Acoust Speech Signal Process, 1989, 37: 720–741
Kay S M, Shaw A K. Frequency estimation by principal component AR spectral estimation method without eigendecomposition. IEEE Trans Acoust Speech Signal Process, 1988, 36: 95–101
Davila C E, Azmoodeh M. Efficient estimation of the signal subspace without eigendecomposition. IEEE Trans Signal Process, 1994, 42: 236–239
Xu G H, Kailath T. Fast subspace decomposition. IEEE Trans Signal Process, 1994, 42: 539–551
Barabell A. Improving the resolution performance of eigenstructure-based direction-finding algorithms. In: Proceedings of IEEE International Conference on Acoustics, Speech, and Signal Processing, Boston, 1983. 336–339
Roy R, Kailath T. ESPRIT-estimation of parameters via rotational invariance techniques. IEEE Trans Acoust Speech Signal Process, 1989, 37: 984–995
Belloni F, Richter A, Koivunen V. DOA estimation via manifold separation for arbitrary array structures. IEEE Trans Signal Process, 2007, 55: 4800–4810
Rubsamen M, Gershman A B. Direction-of-arrival estimation for nonuniform sensor arrays: from manifold separation to Fourier domain MUSIC methods. IEEE Trans Signal Process, 2009, 57: 588–599
Li F, Richard J. VMCARO, analysis of Min-Norm and MUSIC with arbitrary array geometry. IEEE Trans Aerosp Electron Syst, 1990, 26: 976–985
Von Neumann J. Functional Operators II: The Geometry of Orthogonal Spaces. Princeton: Princeton University Press, 1950
Kayalar S, Weinert H. Error bounds for the method of alternating projections. Math Control Signal Syst, 1988, 1: 43–59
Halperin I. The product of projection operators. Acta Sci Math, 1962, 23: 96–99
Golub G H, van Loan C F. Matirx Computations. 3rd ed. The Johns Hopkins University Press, 1983
Van Trees H. Optimum Array Processing Optimum Array Processing. Wiley-Intersicence, 2002
Liu J, Liu X Q, Ma X L. First-order perturbation analysis of singular vectors in singular value decomposition. IEEE Trans Signal Process, 2008, 56: 3044–3049
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yan, F., Jin, M. & Qiao, X. Source localization based on symmetrical MUSIC and its statistical performance analysis. Sci. China Inf. Sci. 56, 1–13 (2013). https://doi.org/10.1007/s11432-013-4841-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11432-013-4841-6