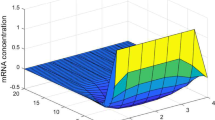
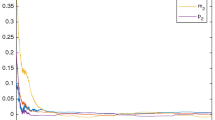
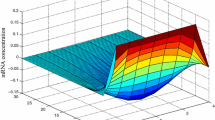
Abstract
The stability of gene regulatory networks has attracted substantial research efforts in the field of systematic biology. Actual gene regulatory networks are always subject to noise interference and disruption to the organism either internally or externally. Specifically, the special case of instantaneous mutation may exist in gene regulatory networks at the mRNA or protein level. Compared with other existing models, a Lévy noise-driven gene regulatory network model has been proved to be more realistic, since it is a powerful tool to describe the above special case. On the basis of previous studies, we developed a theoretical proof of the Lévy noise- driven gene regulatory network, and carried out a large number of numerical simulations for validation. Based on adequate analysis of the simulation examples, the sufficient conditions were investigated and are presented herein to obtain the global asymptotic stability of gene regulatory networks with time-varying delays and Lévy noise.
Similar content being viewed by others
References
Liu W W, He J. Applications of differential equation model in the construction of gene regulatory networks (in Chinese). Chin J Health Stat, 2008, 25: 91–96
Davidson E H, Erwin D H. Gene regulatory networks and the evolution of animal body plans. Science, 2006, 311: 796–800
Somogyi R, Sniegoski C A. Modeling the complexity of genetic networks: understanding multigenic and pleiotropic regulation. Complexity, 1996, 1: 45–63
Guo Y Q. Controllability of Boolean control networks with state-dependent constraints. Sci China Inf Sci, 2016, 59: 032202
Friedman N, Linial M, Nachman I, et al. Using bayesian networks to analyze expression data. J Comput Biol, 2000, 7: 601–620
Hardy S, Robillard P N. Modeling and simulation of molecular biology systems using Petri nets: modeling goals of various approaches. J Bioinf Comput Biol, 2004, 2: 595–613
Ding Z H, Jiang M Y, Chen H B, et al. Petri net based test case generation for evolved specification. Sci China Inf Sci, 2016, 59: 080105
Hu S G, Huang C M, Wu F K. Stochastic Differential Equations. Beijing: Science Press, 2008. 27–30
Chen L, Aihara K. Stability of genctic regulatory networks with time delay. IEEE Trans Circuits Syst I, 2002, 49: 602–608
Wu F X. Stability and bifurcation of ring-Structured genetic regulatory networks with time delays. IEEE Trans Circuits Syst I, 2012, 59: 1312–1320
Pan W, Wang Z D, Gao H J, et al. On multistability of delayed genetic regulatory networks with multivariable regulation functions. Math Biosci, 2010, 228: 100–109
Zhou G L. Stochastic partial differential equations with Lévy jump. Dissertation for the Doctoral Degree. Hunan: Central South University, 2010. 51–78
Zhu Q X. Asymptotic stability in the pth moment for stochastic differential equations with Lévy noise. J Math Anal Appl, 2014, 416: 126–142
Li Z H, Xu W. Asymptotic results for exponential functionals of Lévy processes. arXiv:1601.02363
Curry C, Ebrahimi-Fard K, Malham S J A, et al. Algebraic structures and stochastic differential equations driven by Lévy processes. arXiv: 1601.04880
Wu F X. Delay-independent stability of genetic regulatory networks. IEEE Trans Neural Netw, 2011, 22: 1685–1693
Feng W, Yang S X, Fu W, et al. Robust stability of stochastic genetic regulatory networks with disturbance attenuation. In: Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, 2008. 985–989
Hirata H, Yoshiura S, Ohtsuka T, et al. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feed back loop. Science, 2002, 298: 840–843
Elowitz M B, Levine A J, Siggia E D, et al. Stochastic gene expression in a single cell. Science, 2002, 297: 1183–1186
Raser J M, O’Shea E K. Noise in gene expression: origins, consequences and control. Science, 2005, 309: 2010–2013
Wang Z X, Liu G D, Sun Y H, et al. Robust stability of stochastic delayed genetic regulatory networks. Cogn Neurodyn, 2009, 3: 271–280
Zhang W B, Fang J A, Tang Y. Stochastic stability of Markovian jumping genetic regulatory networks with mixed time delays. Appl Math Comput, 2011, 217: 7210–7225
Zhang W, Tang Y, Fang J A, et al. Exponential cluster synchronization of impulsive delayed genetic oscillators with external disturbances. Chaos, 2011, 21: 1187–1202
Wang Z D, Shu H S, Liu Y R, et al. Robust stability analysis of generalized neural networks with discrete and distributed time delays. Chaos Soliton Fract, 2006, 30: 886–896
Ma Q, Xu S Y, Zou Y, et al. Robust stability for discrete-time stochastic genetic regulatory networks. Nonlinear Anal-Real World Appl, 2011, 12: 2586–2595
Li C G, Chen L N, Aihara K. Stability of genetic networks with SUM regulatory logic: Lur’e system and LMI approach. IEEE Trans Circuits Syst I, 2006, 53: 2451–2458
Wu F X, Zhang W J, Kusalik A J. On robust stability of stochastic genetic regulatory networks with time delays: a delay fractioning approach. IEEE Trans Syst Man Cybern B, 2010, 40: 729–740
Wu H X, Liao X F, Guo S T, et al. Stochastic stability for uncertain genetic regulatory networks with interval time-varying delays. Neurocomputing, 2009, 72: 3263–3276
Castellanos Rubio A, Fernandez Jimenez N, Kratchmarov R. A long noncoding RNA associated with susceptibility to celiac disease. Science, 2016, 352: 91–95
Sun Y H, Feng G, Cao J D. Stochastic stability of Markovian switching genetic regulatory networks. Phys Lett A, 2009, 373: 1646–1652
Zhang W B. Stochastic dynamics analysis of gene regulatory networks. Dissertation for the Doctoral Degree. Shanghai: Donghua University, 2012. 3–30
Ren F L, Cao J D. Asymptotic and robust stability of genetic regulatory networks with time-varying delays. Neuro-computing, 2008, 71: 834–842
Gu K. An integral inequality in the stability problem of time-delay systems. In: Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, 2000. 2805–2810
Boyd S P. Linear Matrix Inequalities in System and Control Theory. Philadelphia: SIAM, 1994. 7–42
Zhu Q X. Stability of stochastic differential equations with Lévy noise. In: Proceedings of the 33rd Chinese Control Conference, Nanjing, 2014. 5211–5216
Oksendal B. Stochastic Differential Equations. 5th ed. New York: Springer-Verlag, 2000. 109–122
Yang Y Q, Zhang X L, Wang X H, et al. Connexin40 nonsense mutation in familial atrial fibrillation. Int J Mol Med, 2010, 26: 605–610
Lin X, Gemel J, Glass A, et al. Connexin40 and connexin43 determine gating properties of atrial gap junction channels. J Mol Cell Cardiol, 2010, 48: 238–245
Chaldoupi S, Loh P, Hauer R N W, et al. The role of connexin40 in atrial fibrillation. Cardiovasc Res, 2009, 84: 15–23
Alonso F, Domingospereira S, Le G L, et al. Targeting endothelial connexin40 inhibits tumor growth by reducing angiogenesis and improving vessel perfusion. Oncotarget, 2016, 7: 14015–14028
Acknowledgements
This work was supported by National Natural Science Foundation of China (Grant No. 61573193) and Joint Key Grant of National Natural Science Foundation of China and Zhejiang Province (Grant No. U1509217).
Author information
Authors and Affiliations
Corresponding author
Additional information
Conflict of interest The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Luo, Q., Gong, Y. & Jia, C. Stability of gene regulatory networks with Lévy noise. Sci. China Inf. Sci. 60, 072204 (2017). https://doi.org/10.1007/s11432-016-0526-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11432-016-0526-8